Categoría: Soluciones

$Z(t) = X(t) -Y(t)$ $Y(t) = h(t)*X(t)$

a) autocorrelación de Z(t)

$E[Z(t_1)Z(t_2)] = E[(X(t_1) - Y(t_1))(X(t_2) -Y(t_2))]$ $= E[X(t_1)(X(t_2) - X(t_1)Y(t_2) - Y(t_1)X(t_2) + Y(t_1)Y(t_2)]$ $= E[X(t_1)(X(t_2)] - E[X(t_1)Y(t_2)] - E[Y(t_1)X(t_2)] + E[Y(t_1)Y(t_2)]$ $= R_X(\tau) - R_{XY}(\tau) - R_{YX}(\tau) + R_Y(\tau)$

b) Densidad espectral de potencia de Z(t)

$Sz(f) = F[R_X(\tau)] - F[R_{XY}(\tau)] - F[R_{YX}(\tau)] + F[R_Y(\tau)]$ $= S_X(f) - S_{XY}(f) - S_{YX}(f) + S_Y(f)$ $= S_X(f) - S_{XY}(f) - S_{XY}^* (f) + S_Y(f)$ $= S_X(f) - H(f) S_{X}(f) - H^* (f) S_{X}(f) + S_Y(f)$ $= [1 - H(f) - H^* (f) + |H(f)|^2] S_X(f)$ $= [1 - 2Re[H(f)] + |H(f)|^2 ] S_X(f)$ $Sz(f) = |1 - H(f)|^2 S_X(f)$

$X(t) = A_1 \cos (\omega _0 t + \theta _1) + A_2 \cos (\sqrt{2}\omega_0 t + \theta _2)$
Las variables aleatorias Θ son uniformes en [0,2π], por lo que sus funciones de densidad de probabilidad son iguales a:
$f_{\theta _1} (\theta _1) = f_{\theta _2}(\theta _2) = \frac{1}{2\pi}$

a) valor esperado:

$E[X(t)] = E[A_1 \cos (\omega _0 t + \theta _1) + A_2 \cos (\sqrt{2}\omega_0 t + \theta _2) ]$ $=E[A_1 \cos (\omega _0 t + \theta _1)] + E[A_2 \cos (\sqrt{2}\omega_0 t + \theta _2) ]$

las variables A₁ y Θ₁ son independientes, de la misma forma A₂ y Θ₂, lo que permite separar: E[XY] = E[X][Y]

$=E[A_1]E[\cos (\omega _0 t + \theta _1)] +E[A_2]E[\cos (\sqrt{2}\omega_0 t + \theta _2)]$

y evaluar:

$E[\cos (\omega _0 t + \theta _1)] = \int_{0}^{2\pi} \cos (\omega _0 t + \theta _1) \frac{1}{2\pi} d\theta _1$ $E[g(x)] = \int_{0}^{2\pi} g(x) f(x) dx$ $= \frac{1}{2\pi}\int_{0}^{2\pi} \cos (\omega _0 t + \theta _1) d\theta _1$

que aplicando:

$cos(x \pm y)= cos(x)cos(y) \mp sen(x)sen(y)$ $= \frac{1}{2\pi}\int_{0}^{2\pi} \Big[\cos (\omega _0 t) \cos(\theta _1) - \sin(\omega _0 t)\sin(\theta _1)\Big] d\theta _1$ $= \frac{1}{2\pi}\cos (\omega _0 t) \int_{0}^{2\pi} \cos(\theta _1) d\theta _1 - \frac{1}{2\pi}\sin(\omega _0 t) \int_{0}^{2\pi} \sin(\theta _1) d\theta _1$ $= \frac{1}{2\pi}\cos (\omega _0 t) \sin(\theta _1)\Big|_{0}^{2\pi} - \frac{1}{2\pi}\sin(\omega _0 t) [-\cos(\theta _1)] \Big|_{0}^{2\pi}$ $= \frac{1}{2\pi}\cos (\omega _0 t) [\sin(2\pi)-sin(0)] + \frac{1}{2\pi}\sin(\omega _0 t) [\cos(2\pi) - \cos(0)]$ $E[\cos (\omega _0 t + \theta _1)] = 0$

por lo que, aplicando lo mismo para el siguiente término del integral del valor esperado, se obtiene que:

$E[X(t)] = 0$

---

b) Para el caso de autocorrelación se tiene que:

$E[X(t_1)X(t_2)] =$
$= E\Big[ [A_1 \cos (\omega _0 t_1 + \theta _1) + A_2 \cos (\sqrt{2}\omega_0 t_1 + \theta _2)] .$

$. [A_1 \cos (\omega _0 t_2 + \theta _1) + A_2 \cos (\sqrt{2}\omega_0 t_2 + \theta _2)] \Big]$

multiplicando término a término

$= E[A_1^2 \cos (\omega _0 t_1 + \theta _1) \cos (\omega _0 t_2 + \theta _1)] +$ $E[A_1 A_2 \cos (\omega _0 t_1 + \theta _1) \cos (\sqrt{2}\omega_0 t_2 + \theta _2)] +$ $E[A_2 A_1 \cos (\sqrt{2}\omega_0 t_1 + \theta _2) \cos (\omega _0 t_2 + \theta _1)] +$ $E[A_2^2 \cos (\sqrt{2}\omega_0 t_1 + \theta _2) \cos (\sqrt{2}\omega_0 t_2 + \theta _2)] =$

recordando que, las variables A₁ y Θ₁ son independientes, de la misma forma A₂ y Θ₂, lo que permite separar: E[XY] = E[X][Y]

$= E[A_1^2] E[\cos (\omega _0 t_1 + \theta _1) \cos (\omega _0 t_2 + \theta _1)] +$ $E[A_1 A_2] E[\cos (\omega _0 t_1 + \theta _1) \cos (\sqrt{2}\omega_0 t_2 + \theta _2)] +$ $E[A_2 A_1] E[\cos (\sqrt{2}\omega_0 t_1 + \theta _2) \cos (\omega _0 t_2 + \theta _1)] +$ $E[A_2^2] E[\cos (\sqrt{2}\omega_0 t_1 + \theta _2) \cos (\sqrt{2}\omega_0 t_2 + \theta _2)] =$

Se desarrolla para una parte del segundo término de la suma:
$E[\cos (\omega _0 t_1 + \theta _1) \cos (\sqrt{2}\omega_0 t_2 + \theta _2)] =$

que siendo independiente Θ₁ y Θ₂ E[XY] = E[X][Y]

$= E[\cos (\omega _0 t_1 + \theta _1)] E[\cos (\sqrt{2}\omega_0 t_2 + \theta _2)] = 0$

cuyo primer término es cero, usando el resultado del literal a, y extendido el resultado para el segundo término, lo que reduce la expresión de la autocorrelación a:

$E[X(t_1)X(t_2)] =$ $= E[A_1^2] E[\cos (\omega _0 t_1 + \theta _1) \cos (\omega _0 t_2 + \theta _1)] +$ $+ E[A_2^2] E[\cos (\sqrt{2}\omega_0 t_1 + \theta _2) \cos (\sqrt{2}\omega_0 t_2 + \theta _2)]$

para el primer término:

$E[\cos (\omega _0 t_1 + \theta _1) \cos (\omega _0 t_2 + \theta _1)] =$ $=\frac{1}{2}E\Big[\cos [(\omega _0 t_1 + \theta _1) - (\omega _0 t_2 + \theta _1)] + \cos [(\omega _0 t_1 + \theta _1) +(\omega _0 t_2 + \theta _1)\Big]$ $=\frac{1}{2}E\Big[\cos (\omega _0 (t_1 - t_2)) + \cos (\omega _0 (t_1 + t_2) + 2 \theta _1)\Big]$ $=\frac{1}{2}E\Big[\cos (\omega _0 (t_1 - t_2)) \Big] + E\Big[\cos (\omega _0 (t_1 + t_2) + 2 \theta _1)\Big]$

del literal a, el segundo término se vuelve cero:

$=\frac{1}{2}E[\cos (\omega _0 (t_1 - t_2)) ]$

extendiendo el resultado para el segundo término de la autocorrelación:

$E[X(t_1)X(t_2)] = \frac{1}{2} E\Big[A_1^2\Big] E\Big[\cos (\omega _0 (t_1 - t_2)) \Big] +$ $+ \frac{1}{2} E\Big[A_2^2\Big] E\Big[\cos (\sqrt{2}\omega _0 (t_1 - t_2)) \Big]$

que se resume que la media es cero, constante, y que la autocorrelación depende solo de la diferencias de tiempo |t₁-t₂| = τ, por lo que el proceso se clasifica como estacionario en el sentido amplio WSS.

Recuerde que A₁ y A₂ son tipo Gaussianas, por lo que E[A₁²] es una constante.

Se establecen los casos posibles para los servidores, (rápido, lento):

0, 00, ambos servidores están libres
1, 10, el servidor lento está libre
2, 01, el servidor rápido esta libre
3, 11, ambos servidores están ocupados

b) … si los clientes al llegar y encontrar los servidores libres, se los envía al servidor más rápido.

las ecuaciones de balanceo son:

Sale del estado = Ingresa al estado
P00 λ = μ P01 + 2μ P10
P01 (λ + μ)  =  2μ P11
P10 (λ+ 2μ) = λ P00 + μ P11
P11 (μ + 2μ) = λ P01 + λ P10

P00 + P01 + P10 + P11 = 1

c) … si los clientes al llegar encuentran los servidores libres, se los envía a cualquiera con la misma probabilidad.

las ecuaciones de balanceo son:

Sale del estado = Ingresa al estado
P00 (λ/2 + λ/2) = μ P01 + 2μ P10
P01 (λ + μ)  =  (λ/2) P00 + 2μ P11
P10 (λ+ 2μ) = (λ/2) P00 + μ P11
P11 (μ + 2μ) = λ P01 + λ P10

P00 + P01 + P10 + P11 = 1

Tarea: Resolver los sistemas de ecuaciones.

Definiciones para el problema para:

un dia cualquiera:    Parte operando A ó B:
        falla:     a
        sigue operando:  (1-a)
    Parte en reparación A ó B:
        se repara:      b
        sigue en reparación: (1-b)

Estados Xn:
0: No existen partes operativas/ todas fallaron
1: Una parte operativa/ una con falla
2: Dos partes operando/ no existen fallas

El diagrama a plantear con tres estados es:

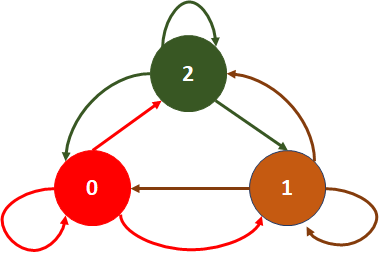
Considera los eventos con las dos partes, estén operativas o dañadas. Los cambios, transición o pasos se consideran desde un dia para el siguiente día:

estado 0:
  sigue en 0, en reparación A y en reparacion B: 
            (1-b)(1-b) = (1-b)2
  pasa a 2, se repara A y se repara B: b*b = b2
  pasa a 1, se repara A y B sigue en reparación, ó,
            se repara B y A sigue en reparación:
            b(1-b) + (1-b)b = 2b(1-b)

estado 1:
  sigue en 1, no falla la operativa y 
            la otra sigue en reparación, ó,
            falla la operativa y 
            se repara la que estaba con falla 
            (1-a)(1-b) + ab
  pasa a 2, no falla la operativa y se repara la otra: 
            (1-a)b 
  pasa a 0, falla la operativa y 
            la otra sigue en reparación: a(1-b)

estado 2:
  sigue en 2: no falla ninguna: (1-a)(1-a) = (1-a)2
  pasa a 1: falla A y B sigue operando, ó,
            falla B y A sigue operando: 
            a(1-a)+(1-a)a = 2a(1-a)
  pasa a 0, falla A y falla B: a*a = a2

que al ponerlo en el digagrama, queda:

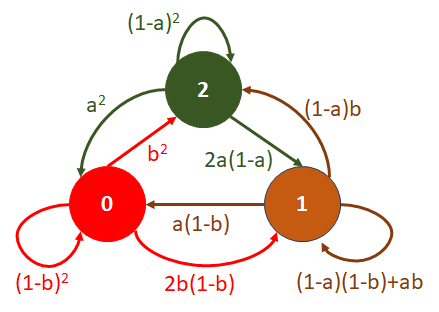
en la matriz de transición de estados de un paso P:

$P = \left( \begin{matrix} (1-b)^2 & 2b(1-b) & b^2 \\ a(1-b) & (1-a)(1-b) + ab & b(1-a) \\ a^2 & 2a(1-a) & (1-a)^2 \end{matrix} \right)$

que reemplazando los valores para a=0.1 y b=0.7 se verifica que las filas suman 1:

$P = \left( \begin{matrix} 0.09 & 0.42 & 0.49 \\ 0.03 & 0.34 & 0.63 \\ 0.01 & 0.18 & 0.81 \end{matrix} \right)$

para la pmf de estado estable o largo plazo Pn:

0.09 Π0 + 0.03 Π1 + 0.01 Π2 = Π0 
0.42 Π0 + 0.34 Π1 + 0.18 Π2 = Π1 
0.49 Π0 + 0.63 Π1 + 0.81 Π2 = Π2

Π0 + Π1 + Π2 = 1  

Resolviendo queda:

Π0 = 0.015625
Π1 = 0.21875
Π2 = 0.765625  

La proyección para n partes indica que los exponentes de la matriz se convertirán en n, y otros términos sin exponentes deben aumentar para incluir las otras opciones.

---

Caso de resolver la matriz con python:

# 3ra Evaluación II Término 2017
# Tema 1
import numpy as np

# INGRESO
a = 0.1
b = 0.7
n = 100
# PROCEDIMIENTO
P = np.array([[(1-b)**2, 2*b*(1-b), b**2],
              [a*(1-b), (1-a)*(1-b)+a*b, b*(1-a)],
              [a**2, 2*a*(1-a), (1-a)**2]])

Pn = np.linalg.matrix_power(P,n)
# SALIDA
print(P)
print(Pn)

los resultados son

[[ 0.09  0.42  0.49]
 [ 0.03  0.34  0.63]
 [ 0.01  0.18  0.81]]
[[ 0.015625  0.21875   0.765625]
 [ 0.015625  0.21875   0.765625]
 [ 0.015625  0.21875   0.765625]]
>>> 

2da Evaluación II Término 2017-2018. Febrero 7, 2018

Tema 4.
$S_x(f)= \frac{N_0}{2}$

$H(f) = \frac{1}{1+j2\pi f}$ $S_{YX}(f) = H(f) S_x(f) = \frac{N_0}{2}\frac{1}{1+j2\pi f}$ $R_{YX}(\tau) = F^{-1} [S_{YX}(f)]$ $= \frac{N_0}{2} F^{-1} \Big[\frac{1}{1+j2\pi f} \Big]$ $R_{YX}(\tau) = \frac{N_0}{2} e^{-\tau} , \tau>0$

---

Autocorrelación de Y(t)

$S_{Y}(f) = |H(f)|^2 S_x(f)$ $= \Big|\frac{1}{1+j2\pi f}\Big| ^2 \frac{N_0}{2}$ $= \Big|\frac{1}{1+(2\pi f)^2}\Big| \frac{N_0}{2}$ $S_{Y}(f) = \frac{N_0}{4} \Big|\frac{2}{1+(2\pi f)^2}\Big|$ $R_{Y}(\tau) = F^{-1} [S_{Y}(f)]$ $= F^{-1} \Big[\frac{N_0}{4} \frac{2}{1+(2\pi f)^2}\ \Big]$ $= \frac{N_0}{4} F^{-1} \Big[\frac{2}{1+(2\pi f)^2}\ \Big]$ $R_{Y}(\tau) = \frac{N_0}{4} e^{-|\tau|}$

---

Potencia promedio

$R_{Y}(0) = \frac{N_0}{4} e^{-|0|} = \frac{N_0}{4}$

2da Evaluación II Término 2017-2018. Febrero 7, 2018

Tema 3.

R_Y(τ)  = R_X(τ) cos(2 π f₀ τ)

R_X(τ) es una función de autocorrelación

S_Y(f) = F[R_X(τ) cos(2 π f₀ τ) ]

=  F[R_X(τ) (e^{j 2π f₀ τ} +e^{-j 2π f₀ τ} )/2]

=  F[R_X(τ) (e^{j 2π f₀ τ} )]/2 + F[R_X(τ) e^{-j 2π f₀ τ} )]/2

=  S_X(f – f₀ )/2 + S_X(f + f₀ )/2

la densidad espectral de potencia se determina como:

$S_X (f) = F[R_X (\tau)]$

Si $R_X(\tau) = \Lambda \Big( \frac{\tau}{T} \Big)$

$S_X(f) = F \Big[\Lambda \Big(\frac{t}{\tau} \Big) \Big]$ $S_X(f) = T [Sa(\pi fT)]^2$

entonces la densidad espectral de potencia del problema se convierte en:

$S_Y (f) = T [Sa(\pi T(f - f_0)]^2 + T [Sa(\pi T(f + f_0)]^2$

para el caso de calcular la potencia promedio R_Y(0) = Rx(0) cos(2 π f₀ 0) = A cos(0) = A.

 

 

2da Evaluación II Término 2017-2018. Febrero 7, 2018

Tema 2.

θ es una variable aleatoria uniforme, distribuida en el rango [-π π].

$f_{\theta} (\theta) = \frac{1}{\pi - (-\pi))} = \frac{1}{2\pi}$

valor esperados X(t)

$X(t) = \cos (\omega t + \theta)$ $E[X(t)] = E[ \cos (\omega t + \theta)]$ $= \int_{-\pi}^{\pi}x(t)f_{\theta}(\theta) d\theta$ $= \int_{-\pi}^{\pi}\cos (\omega t + \theta) \frac{1}{2\pi} d\theta$ $= \frac{1}{2\pi}\sin (\omega t + \theta) \Big|_{-\pi}^{\pi}$ $= \frac{1}{2\pi} [ \sin (\omega t +\pi) -\sin (\omega t -\pi) ]$ $E[X(t)] = 0$

valor esperado Y(t)

$Y(t) = \sin (\omega t + \theta)$ $E[Y(t)] = E[ \sin(\omega t + \theta)]$ $= \int_{-\pi}^{\pi}y(t)f_{\theta}(\theta) d\theta$ $= \int_{-\pi}^{\pi}\sin(\omega t + \theta) \frac{1}{2\pi} d\theta$ $= \frac{1}{2\pi} [-\cos(\omega t + \theta)] \Big|_{-\pi}^{\pi}$ $= \frac{1}{2\pi} [ -\cos(\omega t +\pi) - (-\cos (\omega t -\pi)) ]$ $= \frac{1}{2\pi} [\cos(\omega t -\pi) - \cos (\omega t +\pi) ]$ $E[Y(t)] = 0$

---

Correlación X(t) y Y(t)

$R_{XY}[t,t+\tau] =E[X(t) Y(t+\tau)]$ $=E[\cos (\omega t + \theta) \sin (\omega (t+\tau) + \theta)]$ $=E \Big[ \frac{1}{2}\Big[\sin [(\omega (t+\tau) + \theta) - (\omega t + \theta)] + \sin [(\omega (t+\tau) + \theta) + (\omega t + \theta)] \Big] \Big]$ $=\frac{1}{2}E\Big[\sin (\omega \tau) + \sin (2\omega t+ \omega \tau + 2\theta) \Big]$ $=\frac{1}{2}E \Big[ \sin (\omega \tau) \Big] + \frac{1}{2}E\Big[\sin (2\omega t+ \omega \tau + 2\theta) \Big]$

El primer término no contiene la variable aleatorioa Θ, por lo que se comporta como una constante para el valor esperado.

$=\frac{\sin (\omega \tau)}{2} + \frac{1}{2}\int_{-\pi}^{\pi}\sin (2\omega t+ \omega \tau + 2\theta) \frac{1}{2\pi} d\theta$ $=\frac{\sin (\omega \tau)}{2} - \frac{1}{4\pi}\cos (2\omega t+ \omega \tau + 2\theta) \Big|_{-\pi}^{\pi}$ $=\frac{\sin (\omega \tau)}{2} - \frac{1}{4\pi}\Big[ \cos (2\omega t+ \omega \tau + 2\pi) - \cos (2\omega t+ \omega \tau - 2\pi)\Big]$ $=\frac{\sin (\omega \tau)}{2} - 0$ $R_{XY}[t,t+\tau] =\frac{\sin (\omega \tau)}{2}$

---

$C_{XY}[t,t+\tau] = R_{XY}[t,t+\tau] - E[X(t)]E[Y(t+\tau)]$ $C_{XY}[t,t+\tau] = R_{XY}[t,t+\tau] - 0$ $C_{XY}[t,t+\tau] = \frac{\sin (\omega \tau)}{2}$

---

X(t) y Y(t) son procesos con correlación, pues su covarianza cruzada no es igual a cero para todas las selecciones de muestras de tiempo. Sin embargo, X(t₁) y Y(t₂) son variables aleatorias no correlacionadas para t₁ y t₂ dado que ω( t₂  – t₁ ) = k π, donde k es cualquier número entero.

---

Los valores de mas medias de X(t) = Y(t) =0 son constantes

$R_{X}[t,t+\tau] = E[X(t) X(t+\tau)]$ $=E[\cos (\omega t + \theta) \cos(\omega (t+\tau) + \theta)]$ $=E\Big[\frac{1}{2} \Big[ \cos [(\omega t + \theta) -(\omega (t+\tau) + \theta) ] + \cos[(\omega t + \theta)+(\omega (t+\tau) + \theta)] \Big] \Big]$ $=\frac{1}{2}E\Big[ \cos (\omega \tau ) + \cos(2\omega t + \omega \tau + 2\theta)] \Big]$ $=\frac{1}{2}E\Big[ \cos (\omega \tau )\Big] +\frac{1}{2}E\Big[ \cos(2\omega t + \omega \tau + 2\theta)] \Big]$ $=\frac{\cos (\omega \tau )}{2} \cos (\omega \tau ) +0$

La autocorrelación depende solo de las diferencias de tiempo τ = t₂-t₁

El proceso X(t) clasifica como Estacionario en el sentido amplio.

Tarea: Revisar la autocorrelación para Y(t) para verificar si clasifica como WSS.

2da Evaluación II Término 2017-2018. Febrero 7, 2018

Tema 1. Propuesta de solución

$Y(x) = e^{-\alpha x}$

Siendo X de tipo uniforme entre (0,T]

$f_x(x) = \frac{1}{T}$

Se puede calcular la función de densidad por cada punto de intersecciónal, al trazar una paralela al eje x que pasa por el punto y₀

$f_Y(y) = \sum_k \frac{f_x(x)}{|\frac{dy}{dx}|} \Big|_{x=x_0}$

De la gráfica del enunciado se encuentra que existe un solo punto de intersección  (y₀, x₀).

Para un valor de y₀ se encuentra su valor equivalente en x₀,

$y_0 = e^{-\alpha x_0}$ $\ln (y_0) = \ln (e^{-\alpha x_0})$ $\ln (y_0) = -\alpha x_0$ $x_0 = \frac{\ln (y_0)}{-\alpha}$

la derivada dy/dx será

$\frac{dy}{dx} = -\alpha e^{-\alpha x}$

Reemplazando en la ecuación para f_Y(y):

$f_Y(y) = \frac{\frac{1}{T}}{|-\alpha e^{-\alpha x_0}|}$ $= \frac{1}{T|-\alpha e^{-\alpha \frac{ln(y_0)}{-\alpha}}|}$ $= \frac{1}{T|-\alpha e^{ln(y_0)}|}$ $f_Y(y) = \frac{1}{T\alpha y}$

los valores de x se encuentran entre (0,T], por lo que los valores de y se encuentran:

$y_0 = e^{-\alpha(0)} = 1$ $y_T = e^{-\alpha (T)} = e^{-\alpha T}$

el rango para y se encuentra entre 1 y e^-αT.

La función de distribución acumulada:

$F_Y(y) = \int_{1}^{y} f_Y(y) dy$ $= \int \frac{1}{T\alpha y} dy$ $= \frac{1}{T\alpha} \int \frac{1}{y} dy$ $= \frac{1}{T\alpha} ln(y) \Big|_{1}^{y}$ $= \frac{1}{T\alpha}(ln(y) - ln(1))$ $= \frac{1}{T\alpha}( ln(y) - 0)$ $= \frac{1}{T\alpha}ln(y)$ $F_Y(y) = \frac{ln(y)}{T\alpha}$

Gráfica: Para que la gráfica tenga una forma representativa, α=-1.

La auto-correlación aplica para funciones que dependen del tiempo, con diferencias de tiempo τ.
Para éste caso, no aplica la autocorrelación. tampoco se dispone de otra variable en el problema para realizar la correlación.

---

Script de python para presentar las gráficas del problema

import numpy as np
import matplotlib.pyplot as plt

# INGRESO
alfa = -1
T = 1
# Rango de x
a = 0
b = a + T
# muestreo
m = 100

# PROCEDIMIENTO
funciony = lambda x: np.exp(alfa*x)
pdf = lambda y: 1/(T*np.abs(alfa*y))
cdf = lambda y: np.log(y)/(np.abs(alfa)*T)

x = np.linspace(a,b,m)
yi = funciony(x)

ya = funciony(alfa*a)
yb = funciony(alfa*b)
y = np.linspace(yb,ya,m)

fy = pdf(y)
Fy = cdf(y)

# SALIDA
plt.subplot(311)
plt.plot(x, yi,label='y')
plt.legend()
plt.subplot(312)
plt.plot(y,fy, label='fy')
plt.legend()
plt.subplot(313)
plt.plot(y,Fy, label='Fy')
plt.legend()
plt.show()