2Eva2011TII_T1 LTI CT entrada con cuadratizador

2da Evaluación II Término 2011-2012. 2/Febrero/2012. TELG1001

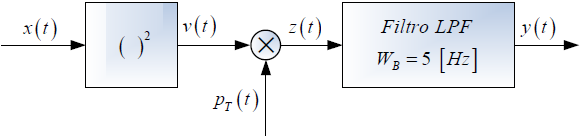
Tema 1. (40 puntos) Una señal de entrada x(t) = sinc (5 πt) es aplicada a un dispositivo cuadratizador, tal com se muestr en la siguiente figura.

$p_T (t) = \sum_{k=-\infty}^{\infty} p_{0.0125} (t-kT_0) ; T_0=0.1[seg]$

La respuesta v(T) del mencionado dispositivo es muestreada mediante la utilización de un tren de pulsos rectangulares P_T(t), tal como se muestra en la figura.

Finalmente a la señal de salida z(t) se le aplica un filtro ideal pasa bajo cuyo ancho de banda es de 5 [Hz].

a. Determinar la energía contenida en la señal x(t).

b. Determinar, esquematizar y etiquetar el espectro de Fourier de v(t). Es decir V(ω) vs ω.

c. Determinar la frecuencia angular fundamental ω₀ y los coeficientes de las series armónicas de Fourier C₀ y C_k para la señal periódica P_T(t), cuya representación es de la siguiente forma:

$p_T (t) = C_0 + \sum_{k=1}^{\infty} C_k \cos (k \omega _0 t - \theta _k)$

d. Determinar, esquematizar y etiquetar el espectro de Fourier de y(t). Es decir, Y(ω) vs ω.

---

Coordinador: Tama Alberto