Se continúa con el ejercicio propuesto en la sección Sistema-Modelo entrada-salida:
Referencia: Lathi ejemplo 2.6 p166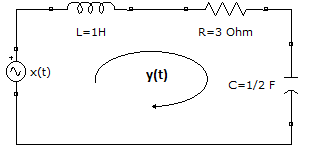
En la entrada de sistema se aplica:
x(t) = 10 e^{-3t} \mu (t)El sistema tiene respuesta a impulso:
h(t) = \big( 2e^{-2t} -e^{-t}\big)\mu (t)El ejemplo es la continuación de lo realizado en respuesta a entrada cero, que tiene la ecuación:
(D^2 + 3D +2)y(t) = Dx(t)El ejercicio se desarrolla en Python de varias formas para obtener el resultado en una gráfica usando:
1. Un sistema LTI con Scipy.signal.lti() y simulado con Scipy.signal.lsim()
2. La integral de convolución con Numpy.convolve()
3. La integral de convolución con algoritmo numérico
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]
1. Un sistema LTI con Scipy.signal.lti() y simulado con Scipy.signal.lsim()
Esta forma de describir el problema, simplifica el desarrollar el ejercicio a partir de la descripción de la ecuación del sistema.
La libreria Scipy.signal permite definir un sistema LTI, usando los coeficientes de la ecuación y condiciones de inicio en cero.
La salida y(t) se calcula con una versión muestreada xi de la función de entrada x(t) a partir del tiempo muestreado en el intervalo [a,b].
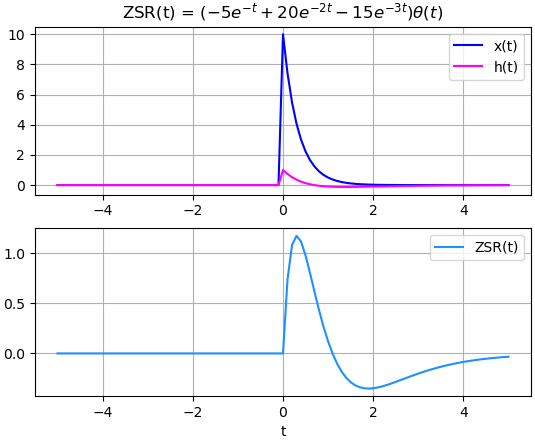
En el algoritmo se incorpora la gráfica de la función de transferencia h(t) como referencia.
# Sistema lineal usando scipy.signal # Q(D)y(t)=P(D)x(t) # ejemplo: (D^2+3D+2)y(t)=(D+0)x(t) import numpy as np import scipy.signal as senal # INGRESO # tiempo [a,b] a = 0 ; b = 5 ; muestras=101 # Señal de entrada u = lambda t: np.piecewise(t,t>=0,[1,0]) x = lambda t: 10*np.exp(-3*t)*u(t) # Sistema LTI # coeficientes Q P de la ecuación diferencial Q = [1., 3., 2.] P = [1., 0.] # condiciones de inicio [y'0,y0] inicio = [0.,0.] # PROCEDIMIENTO ti = np.linspace(a, b, muestras) xi = x(ti) sistema = senal.lti(P,Q) [t_y, yi, yc] = senal.lsim(sistema, xi, ti, inicio) [t_h, hi] = sistema.impulse(T = ti) # SALIDA - GRAFICA import matplotlib.pyplot as plt plt.subplot(211) plt.suptitle('Respuesta a estado cero') plt.plot(ti, xi, color='blue', label='x(t)') plt.plot(t_h, hi, color='red', label='h(t)') plt.legend() plt.grid() plt.subplot(212) plt.plot(t_y, yi, color='magenta', label='y(t)') # plt.plot(t_y, yc[:,0], 'g-.', label='y(t)') # plt.plot(t_y, yc[:,1], color='orange', label='y0(t)') plt.xlabel('t') plt.legend() plt.grid() plt.show()
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]
2. La integral de convolución con Numpy.convolve()
El algoritmo requiere la expresión de las funciones x(t) y h(t) para determinar y(t). Se realiza el cálculo de la convolución, que para aproximar a la integral requiere multiplicar por dt.
Note que debe mantener el valor dt pequeño, en el ejercicio se ha definido como 0.01 que corresponden a casi 1000 muestras en el intervalo [-5,5].
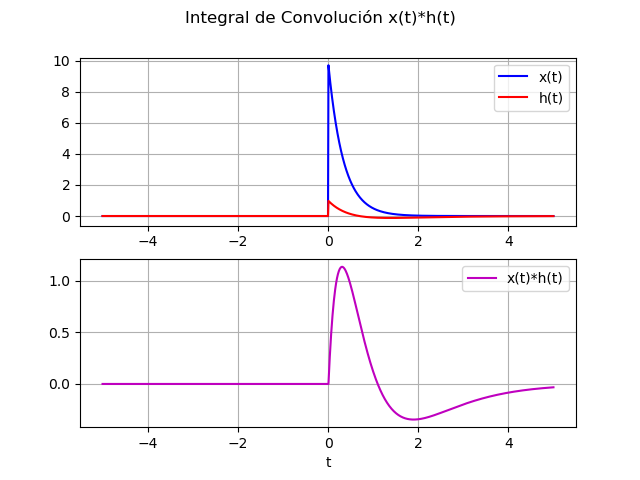
Para usar la función np.convolve(), debido a la naturaleza numérica del algoritmo, se requieren muestras en tiempos, simétricos alrededor de cero. Al mostrar la gráfica, se puede prescindir de la sección negativa, sin embargo, para recordarlo se ha dejado la parte negativa del intervalo de tiempo.
# Señales contínuas en convolución # Compare con el algoritmo en forma discreta # Lathi ejemplo 2.6 p166 import numpy as np import matplotlib.pyplot as plt # INGRESO u = lambda t: np.heaviside(t,1) # u = lambda t: np.piecewise(t,t>=0,[1,0]) x = lambda t: 10*np.exp(-3*t)*u(t) h = lambda t: (2*np.exp(-2*t)-np.exp(-t))*u(t) # tiempo [a,b] simétrico alrededor de 0 b = 5 ; a = -b dt = 0.01 # PROCEDIMIENTO ti = np.arange(a,b+dt,dt) xi = x(ti) hi = h(ti) # Integral de Convolucion x[t]*h[t] # corrección de magnitud por dt para en integral yi = np.convolve(xi,hi,'same')*dt # SALIDA - GRAFICA plt.suptitle('Integral de Convolución x(t)*h(t)') plt.subplot(211) plt.plot(ti,xi,'b', label='x(t)') plt.plot(ti,hi,'r', label='h(t)') plt.legend() plt.grid() plt.subplot(212) plt.plot(ti,yi,'m', label='x(t)*h(t)') plt.xlabel('t') plt.legend() plt.grid() plt.show()
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]
3. La integral de convolución con algoritmo numérico
Esta sección desarrolla el algoritmo para la integral de convolución, tomando paso a paso las operaciones para obtener la gráfica del resultado.
El algoritmo se presenta con propósitos didácticos, pues parece ser un poco más lento debido a que se realizan las operaciones de forma básica (interpretada) de Python. La función np.convolve() usa elementos compilados a lenguaje de maquina que se ejecutan de forma más eficiente.
Note que la única sección que cambia es la de convolución, por lo que la gráfica de salida es la misma que la sección anterior:
# Señales contínuas en convolución. Algoritmo numérico. # compare con el algoritmo en forma discreta # Lathi ejemplo 2.6 p166 import numpy as np import matplotlib.pyplot as plt # INGRESO u = lambda t: np.heaviside(t,1) # u = lambda t: np.piecewise(t,t>=0,[1,0]) x = lambda t: 10*np.exp(-3*t)*u(t) h = lambda t: (2*np.exp(-2*t)-np.exp(-t))*u(t) # tiempo [a,b] simétrico alrededor de 0 b = 5 ; a = -b dt = 0.01 # PROCEDIMIENTO ti = np.arange(a,b+dt,dt) xi = x(ti) hi = h(ti) # Integral de Convolución x[t]*h[t] muestras = len(xi) yi = np.zeros(muestras, dtype=float) for i in range(0,muestras): suma=0 for k in range(0,muestras): suma = suma + x(ti[k])*h(ti[i]-ti[k]) yi[i]= suma*dt # SALIDA - GRAFICA plt.suptitle('Integral de Convolución x(t)*h(t)') plt.subplot(211) plt.plot(ti,xi,'b', label='x(t)') plt.plot(ti,hi,'r', label='h(t)') plt.legend() plt.grid() plt.subplot(212) plt.plot(ti,yi,'m', label='x(t)*h(t)') plt.xlabel('t') plt.legend() plt.grid() plt.show()
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]