Publicado en

1Eva2010TI_T2 LTI CT diagrama de bloques para H(s)

1ra Evaluación I Término 2010-2011. 8/Julio/2010. TELG1001

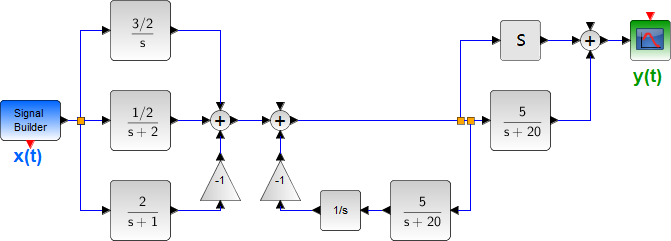
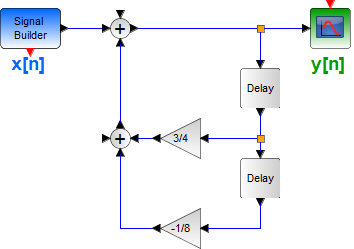
Tema 2. (25 puntos) Considere la existencia de un sistema, cuyo esquema del diagrama de bloques en el dominio de la frecuencia compleja, que relaciona la entrada-salida del mismo, es el siguiente:

Determinar:

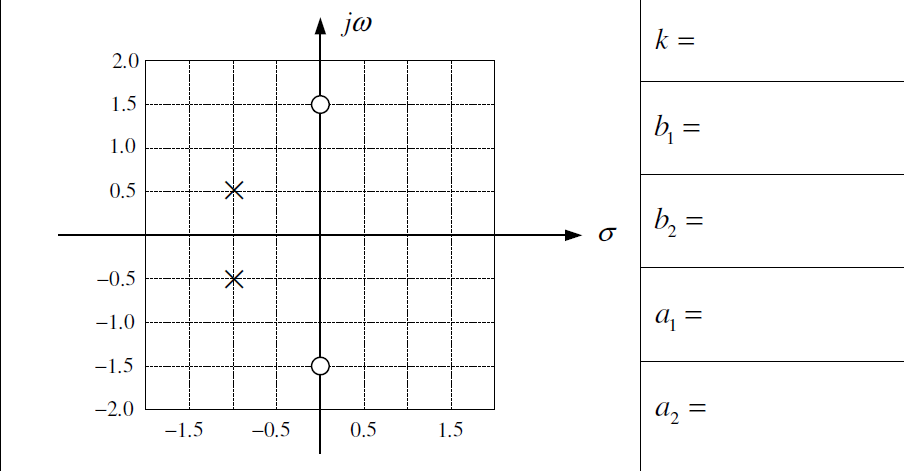
a. La función de transferencia H(s) del mencionado sistema y esquematizar en el plano complejo los polos y ceros. Comente sobre la estabilidad de este sistema, justificando su respuesta.

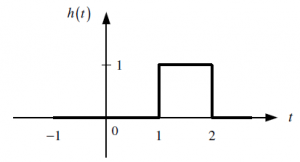
b. La respuesta impulso h(t) de dicho sistema, y la obtención de su valor inicial y final a partir de la aplicación del TVI y TVF.

c. La ecuación diferencial de coeficientes constantes que representa al referido sistema.

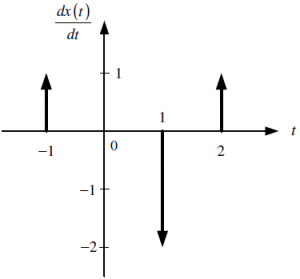
d. La respusta que se obtendría si la exitación es:

x(t) = e^{-3t} \mu(t)
Publicado en

1Eva2010TI_T1 LTI CT respuesta estado cero desde dx(t)/dt

1ra Evaluación I Término 2010-2011. 8/Julio/2010. TELG1001

Tema 1. (25 puntos) Un estudiante de la materia Sistemas Lineales, ha determinado que la representación esquemática de la respuesta impulso h(t), de un sistema LTI-CT es aquella que se muestra en la siguiente figura.

Si se conoce la derivada de la entrada de dicho sistema, esto es dx(t)/dt, determine y esquematice su respuesta de estado cero, es decir:

y(t) = x(t)⊗h(t)

Publicado en

1Eva2009TII_T3 LTI CT y(t) desde h(t) y x(t) con términos escalón desplazados

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 3. (20 puntos) Suponga que la entrada x(t) y la respuesta impulso de un sistema LTI-CT están dadas por:

x(t) = 2 μ(t-1) – 2 μ(t-3)

h(t) = μ(t+1) – 2 μ(t-1) + μ(t-3)

a. Determine y esquematice la salida de dicho sistema, y encuentre la energía total de y(t)

b. ¿El sistema es BIBO estable? justifique su respuesta

Publicado en

1Eva2009TII_T2 LTI DT bloques, respuesta impulso y paso

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 2. (20 puntos) Un estudiante del curso de Sistemas Lineales ha encontrado que un determinado sistema LTI-DT causal, en el dominio del tiempo tiene la siguiente representación:

Determinar:

a. La respuesta impulso h[n]

b. La respuesta de paso s[n]

c. ¿Es el sistema BIBO estable?, justifique su respuesta.

Publicado en

1Eva2009TII_T1 LTI CT diagrama canónico y respuesta a impulso

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 1. (20 puntos) Un estudiante del curso de Sistemas Lineales ha encontrado que un determinado sistema puede ser realizable mediante el diagrama canónico mostrado en la siguiente figura.

Determinar,

a. La función de transferencia del mencionado sistema

b. su respuesta impulso h(t)

c. ¿Qué puede decir acerca de la estabilidad interna y externa?

Referencia: Ejemplo 3, LTIC Laplace – Diagramas de bloques con «1/s»

Publicado en

1Eva2009TII_T5 LTI DT bloques H[z] en serie

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 5. (20 puntos) El sistema que se muestra en la siguiente figura, es el resultante de la combinación de dos subsistemas conectados en cascada.

Determinar:

1. Las respuestas impulso de cada subsistema y del sistema completo, es decir h1[n], h2[n], h[n].

h1[n]
h2[n]
h[n]

2. Su respuesta y[n]=s]n], expresada a la mínima expresión frente a la siguiente excitación x[n]=μ[n], esquematícela.

Publicado en

1Eva2009TII_T4 LTI CT con entrada x(t) tipo coseno

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 4. (20 puntos) El diagrama de polos y ceros de un sistema de segundo orden cuya función de transferencia H(s) es mostrado en la siguiente figura, donde se conoce que la respuesta DC de este sistema es -1. es decir H(j0)=-1.

a. Conociendo el hecho que:

H(s) = \frac{k (s^2 + b_1 s + b_2)}{s^2 + a_1 s + a_2}

determinar el valor de las constantes k, b1,b2, a1 y a2.

b. Encontrar la respuesta y(t) que este sistema tendría, frente a la siguiente entrada:

x(t) = 4+\cos \Big(\frac{1}{2}t +\frac{\pi}{3}\Big)

c. Comente justificadamente acerca de la estabilidad interna y externa del mencionado sistema.