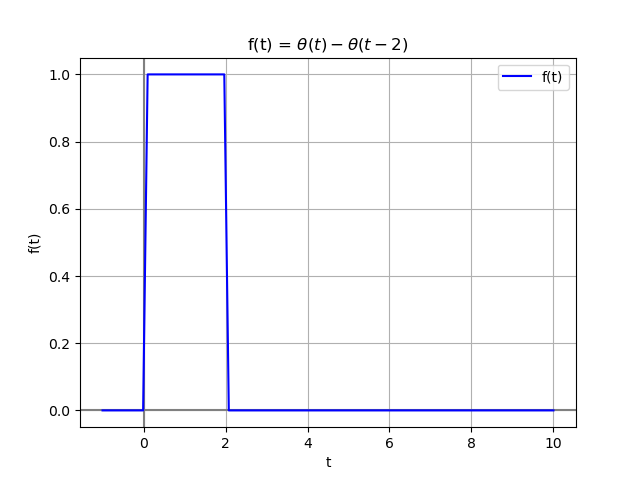
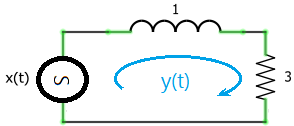
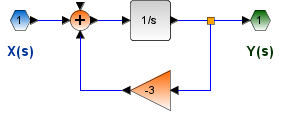
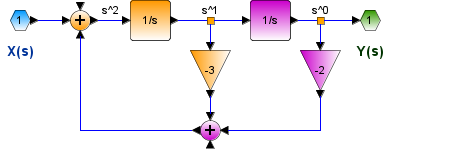
Referencia: Lathi ejemplo 4 p330, Hsu literal C. p112
Las fracciones parciales facilitan usar la Transformada Inversa de Laplace al presentar la expresión de ‘s’, H(s), X(s) o Y(s) como una suma de términos más simples. Los términos de las fracciones parciales permiten analizar los términos por medio de los polos del denominador. La expresión suma de términos buscada antes de usar la tabla de Transformada Inversa de Laplace tiene la forma:
\frac{P(s)}{Q(s)} = \frac{ceros(1)}{s - polos(1)}+\frac{ceros(2)}{s - polos(2)}+\text{ ... } \text{ ... }+\frac{ceros(n)}{s - polos(n)}+ganancia(s)Cuando se presentan funciones de transferencia con términos exponenciales sym.exp(-a*s), las instrucciones para polinomio sym.apart() para fraccciones parciales sym.factors() se encuentran limitadas por tener términos sym.exp(-a*s). Se propone crear una función que agrupe los términos por cada término sym.exp(-a*s) y aplique a cada grupo fracciones parciales o factores.
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 1. Fracciones parciales con Polos reales no repetidos
Referencia: Hsu problema 3.17a p137, Lathi ejemplo 4.3a p338, Oppenheim ejemplo 9.9 p671
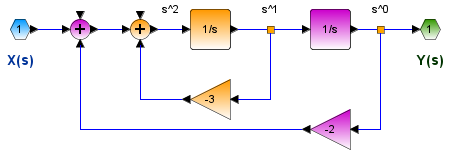
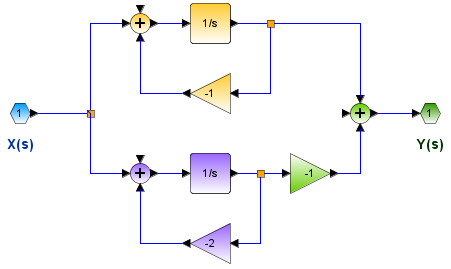
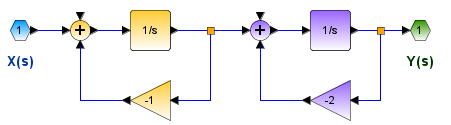
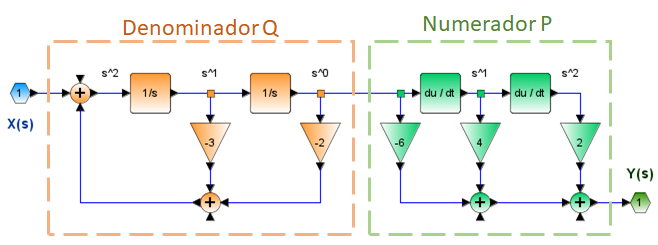
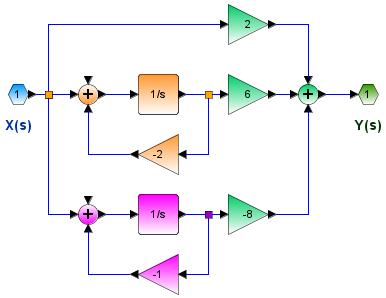
El ejemplo muestra como separar el sistema mostrado en partes más simples usando fracciones parciales:
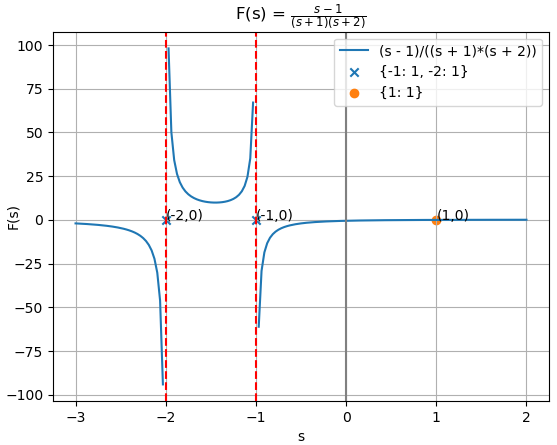
H(s) = \frac{2s+4}{s^2 +4s+3}Ejemplo 1. Desarrollo analítico con el método de Heaviside para fracciones parciales
Las raíces para el polinomio Q del denominador son -1 y -3, por lo que se crea la expresión general como:
H(s)= 2\frac{s+2}{(s+1)(s+3)} = \frac{k_1}{s+1} + \frac{k_2}{s+3}Se aplica el método de «cubrir» de Heaviside para encontrar el valor de k1 , consiste en cubrir el término (s+1) y evaluar la expresión con s=-1.
k_1= 2\frac{s+2}{\cancel{(s+1)}(s+3)}\Bigg|_{s=-1 }= 2\frac{(-1)+2}{((-1)+3)} = 2\frac{1}{2} = 1de forma semejante se procede para el valor de k2,
k_2= 2\frac{s+2}{(s+1)\cancel{(s+3)}} \Bigg|_{s=-3 }= 2\frac{(-3)+2}{((-3)+1)} = 2\frac{-1}{-2} = 1teniendo el resultado de las fracciones parciales,
H(s) = \frac{1}{s+1} + \frac{1}{s+3}usando la tabla de transformadas de Laplace
h(t) = \Big( e^{-t} + e^{-3t} \Big) \mu (t)Ejemplo 1 Fracciones parciales con Sympy-Python
Para la expresión de la función de transferencia, con Sympy se crean los polinomios del numerador Ps y denominador Qs.
# INGRESO s = sym.Symbol('s') Ps = 2*s + 4 # 1+0*s cuando es constante Qs = s**2 + 4*s + 3 Hs = Ps/Qs
Usar H(s)=P(s)/Q(s) permite disponer de una sola expresión de ‘s’ y obtener las fracciones parciales con sym.apart(). En los ejercicios por bloques, las fracciones parciales representan como bloques en paralelo.
Otra forma de expresar H(s) es mediante los factores que usan P_polos y Q_ceros usando la instrucción sym.factors(). En los ejercicios por bloques los factores se representan como bloques en serie.
Las fracciones parciales facilitan obtener la inversa de la transformada de Laplace con términos más simples que pueden ser usados con sym.inverse_laplace_transform(term_suma,s,t), o para usar la tabla de Transformadas de Laplace.
H(s): 2*s + 4 ------------ 2 s + 4*s + 3 H(s) como fracciones parciales 1 1 ----- + ----- s + 3 s + 1 H(s) como factores de polos y ceros 2*(s + 2) --------------- (s + 1)*(s + 3) >>>
Instrucciones en Python
# Fracciones parciales de H(s) con Sympy # Ps es numerador, Qs es denominador import sympy as sym # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) Ps = 2*s + 4 Qs = s**2 + 4*s + 3 # Ps = 2*s**2+5 # Qs = s**2 + 3*s + 2 # Ps = 8*s+10 # Qs = (s+1)*((s+2)**3) # Ps = 6*(s+34) # Qs = s*(s**2+10*s+34) Hs = Ps/Qs # PROCEDIMIENTO # fracciones parciales Hs_fp = sym.apart(Hs,s) # factores Hs_fc = sym.factor(Hs,s) # SALIDA print('H(s):') sym.pprint(Hs) print('\n H(s) como fracciones parciales ') sym.pprint(Hs_fp) print('\n H(s) como factores de polos y ceros ') sym.pprint(Hs_fc)
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 2. Fracciones parciales con grados iguales de P y Q
Referencia: Lathi ejemplo 4.3b p338, Hsu ejercicio 3.20 p140, Oppenheim ejemplo 9.36 p716
H(s) = \frac{2s^2 +5}{s^2 +3s+2}Ejemplo 2 Desarrollo analítico con el método de Heaviside para fracciones parciales
Se observa que los grados de P y Q son iguales, por lo que se toma como ganancia el coeficiente de mayor grado en el numerador. Se obtiene la raíz del denominador Q y se reescribe como
H(s) = \frac{2s^2+5}{(s+1)(s+2)} = 2 + \frac{k_1}{s+1} +\frac{k_2}{s+2} k_1 = \frac{2s^2+5}{\cancel{(s+1)}(s+2)} \Bigg|_{s=-1} = \frac{2(-1)^2+5}{((-1)+2)} = 7 k_2 = \frac{2s^2+5}{(s+1)\cancel{(s+2)}}\Bigg|_{s=-2} = \frac{2(-2)^2+5}{((-2)+1)} = -13obteniendo:
H(s) = 2 + \frac{7}{s+1} -\frac{13}{s+2}El cambio al dominio de tiempo se realiza término a término usando la tabla de transformadas de Laplace
H(t) = 2 \delta (t) +\big( 7 e^{-t} -13 e^{-2t} \big) \mu (t)Ejemplo 2 Desarrollo con Sympy-Python
Al algoritmo del ejercicio anterior se modifica solo el bloque de ingreso con las expresiones para numerador y denominador:
Ps = 2*s**2+5 Qs = s**2 + 3*s + 2 Hs = Ps/Qs
con lo que se obtiene el resultado:
H(s):
2
2*s + 5
------------
2
s + 3*s + 2
H(s) como fracciones parciales
13 7
2 - ----- + -----
s + 2 s + 1
H(s) como factores de polos y ceros
2
2*s + 5
---------------
(s + 1)*(s + 2)
>>>
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 3. Fracciones parciales con raíces repetidas
Referencia: Lathi ejemplo 4.3d p342
H(s) = \frac{8s+10}{(s+1)(s+2)^3}la forma de la expresión para el algoritmo es
Ps = 8*s+10 Qs = (s+1)*((s+2)**3) Hs = Ps/Qs
por lo que el modelo de fracciones parciales es:
H(s) = \frac{k_1}{s+1}+\frac{k_2}{(s+2)^3}-\frac{k_3}{(s+2)^2}-\frac{k_4}{s+2}El desarrollo analítico se deja como tarea para comprobar sus resultados con el algoritmo. Use el método de «cubrir» de Heaviside para obtener las fracciones parciales.
H(s) = \frac{2}{s+1}+\frac{6}{(s+2)^3}-\frac{2}{(s+2)^2}-\frac{2}{s+2}Se usa el ejemplo, para comprobar el algoritmo de las secciones anteriores, obteniendo los resultados siguientes,
H(s):
8*s + 10
----------------
3
(s + 1)*(s + 2)
H(s) como fracciones parciales
2 2 6 2
- ----- - -------- + -------- + -----
s + 2 2 3 s + 1
(s + 2) (s + 2)
H(s) como factores de polos y ceros
2*(4*s + 5)
----------------
3
(s + 1)*(s + 2)
>>>
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
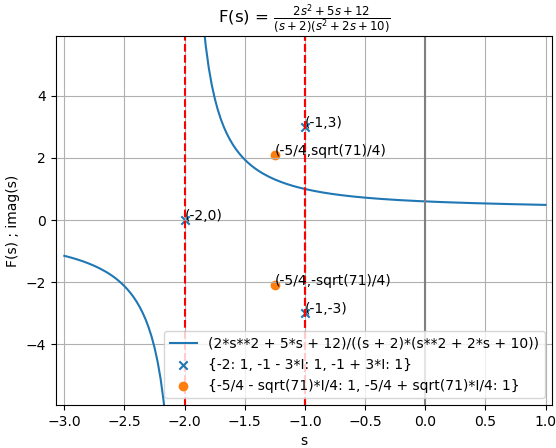
Ejemplo 4. H(s) con Fracciones parciales y polos de tipo complejo
Referencia: Lathi ejemplo 4.3c p340
H(s) = \frac{6(s+34)}{s(s^2+10s+34)}la forma de la expresión para el algoritmo es
Ps = 6*(s+34) Qs = s*(s**2+10*s+34) Hs = Ps/Qs
Ejemplo 4 Desarrollo analítico
Se simplifica la expresión de H(s) usando las raíces reales en las fracciones parciales de la forma:
H(s) = \frac{6(s+34)}{s(s^2+10s+34)} = \frac{k_1}{s} + \frac{As+B}{s^2+10s+34}usando el método de Heaviside, se obtiene k1
k_1 = \frac{6(s+34)}{\cancel{s}(s^2+10s+34)}\Big|_{s=0} =\frac{6(0+34)}{(0^2+10(0)+34)} = \frac{6(34)}{34}=6 \frac{6(s+34)}{s(s^2+10s+34)} = \frac{6}{s} + \frac{As+B}{s^2+10s+34}se simplifican las fracciones al multiplicar ambos lados por s(s2+10s+34)
6(s+34) = 6(s^2+10s+34) + (As+B)s 6s+204 = 6s^2+60s+204 + A s^2+Bs 6s+204 = (6+A)s^2+(60+B)s+204se puede observar que 6+A=0, por lo que A=-6.
También se tiene que 60+B=6, por lo que B=-54
quedando la expresión como:
Observando la tabla de transformadas de Laplace se compara la expresión con las filas 12c y 12d se usan los parámetros de:
\frac{As+B}{s^2+2as+c}A= -6, B=-64, a=5, c = 34
y se calculan:
con lo que se puede escribir la transformada inversa de Laplace para h(t) como
h(t) = [6+10e^{-5t}\cos (3t--0.9272)] \mu (t)o la otra forma de expresión usando la fila 12d de la tabla
Ejemplo 4 Desarrollo con Sympy-Python
Incorporando las instrucciones para identificar si el denominador tiene raíces complejas, se asignan los valores de los parámetros necesarios en un diccionario de variables, obteniendo como resultado,
H(s):
6*s + 204
------------------
/ 2 \
s*\s + 10*s + 34/
H(s) como fracciones parciales
6*(s + 9) 6
- -------------- + -
2 s
s + 10*s + 34
H(s) como factores de polos y ceros
6*(s + 34)
------------------
/ 2 \
s*\s + 10*s + 34/
>>>
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
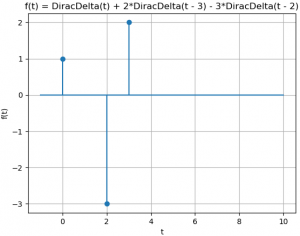
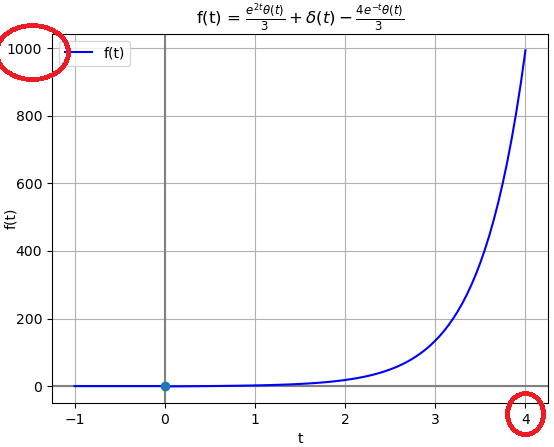
Ejemplo 5. Con suma de términos y exponenciales de retraso en tiempo
H(s) = \frac{s+2}{s-1}+ \frac{e^{-2s}}{s-2}la expresión para el algoritmo se escribe como:
Hs = ((s+2)/(s-1)) + sym.exp(-2*s)/(s-2)
Para el segundo término que tiene un exponencial, no se puede aplicar directamente la instrucción sym.apart(Hs,s) al no ser reconocida como tipo polinomio. Para continuar se debe separar el término sym.exp() del resto de la expresión, y se podrá aplicar fracciones parciales a esa parte, para luego volver a poner el término.
Para facilitar el desarrollo del algoritmo, se recomienda empezar a analizar una expresión mas simple, como solamente el segundo término de la suma.
Implementando una función para tratar este asunto en la parte de fracciones parciales y en el cálculo de polos, se obtiene el resultado,
H(s):
-2*s
s + 2 e
----- + -----
s - 1 s - 2
H(s) en fracciones parciales
-2*s
3 e
1 + ----- + -----
s - 1 s - 2
Al aplicar fracciones parciales se tendrán términos más simples para obtener la Transformada Inversa de Laplace. Aunque cada término de la fracción parcial se multiplica por el exponencial, se deberá recordar este detalle cuando se calculan los polos de la expresión.
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
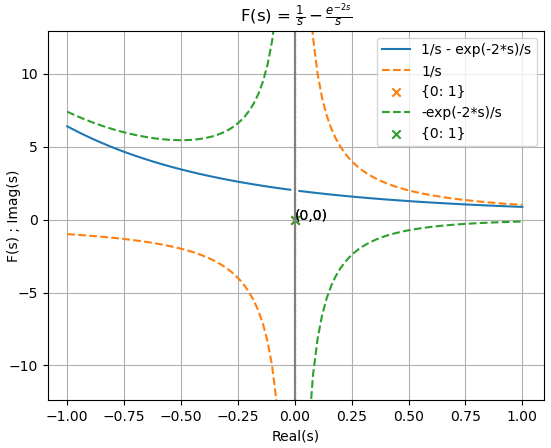
Fracciones Parciales para F(s) con exponencial s o retraso en tiempo
Se crea una función para realizar las fracciones parciales agrupadas por términos exp() y aplicar a esta expresión separada en factores de suma la transformada de Laplace desde la tabla.
X(s) = \frac{s+2}{s-1} + \frac{e^{-2s}}{s-2}Fs = ((s+2)/(s-1)) + sym.exp(-2*s)/(s-2)
se aplica a la expresión sin sym.exp()
X(s) = 1+\frac{3}{s-1} + \frac{e^{-2s}}{s-2} F(s):
-2*s
s + 2 e
----- + -----
s - 1 s - 2
H(s) como fracciones parciales
-2*s
3 e
1 + ----- + -----
s - 1 s - 2
H(s) como factores de polos y ceros
-2*s
s + 2 e
----- + -----
s - 1 s - 2
>>>
Instrucciones en Python
# Fracciones parciales separadas por sym.exp(-a*s) # Factores de polos y ceros separad0s por sym.exp(-a*s) import sympy as sym # INGRESO t = sym.Symbol('t', real=True) s = sym.Symbol('s') Fs = ((s+2)/(s-1)) + sym.exp(-2*s)/(s-2) #Fs = (1/s)*(1-sym.exp(-2*s)) #Hs = sym.exp(s)/s - 2*sym.exp(-s)/s + sym.exp(-3*s)/s #Xs = 2*sym.exp(-s)/s - 2*sym.exp(-3*s)/s #Fs = Hs*Xs #Fs = -sym.exp(-5*s - 10)/(3*s + 6) + 4/(3*s + 6) # PROCEDIMIENTO def apart_s(Fs): '''expande Fs en fracciones parciales considera términos con sym.exp multiplicados ''' # convierte a Sympy si es solo constante Fs = sym.sympify(Fs) # simplifica operación H(s)*x(s) Fs = sym.expand_power_exp(Fs) Fs = sym.expand(Fs, powe_exp=False) # reagrupa Fs term_sum = sym.Add.make_args(Fs) Fs_0 = 0*s for term_k in term_sum: term_k = sym.simplify(term_k) term_k = sym.expand_power_exp(term_k) Fs_0 = Fs_0 + term_k # tabula sym.exp(-s) en lista_exp lista_exp = list(Fs_0.atoms(sym.exp(-s))) if len(lista_exp)>0: # elimina constantes for k in lista_exp: if not(k.has(s)): # es constante lista_exp.remove(k) # separados por lista_exp separados = sym.collect(Fs_0,lista_exp,evaluate=False) # fracciones parciales Fs_fp = 0 for k in separados: Fs_k = sym.apart(separados[k],s) Fs_fp = Fs_fp + k*Fs_k return(Fs_fp) def factor_exp(Fs): '''expande Fs en factores por sym.exp(-a*s) considera términos con sym.exp multiplicados ''' # convierte a Sympy si es solo constante Fs = sym.sympify(Fs) # simplifica operación H(s)*x(s) Fs = sym.expand_power_exp(Fs) Fs = sym.expand(Fs, powe_exp=False) # reagrupa Fs term_sum = sym.Add.make_args(Fs) Fs_0 = 0*s for term_k in term_sum: term_k = sym.simplify(term_k) term_k = sym.expand_power_exp(term_k) Fs_0 = Fs_0 + term_k # tabula sym.exp(-s) en lista_exp lista_exp = list(Fs_0.atoms(sym.exp(-s))) if len(lista_exp)>0: # elimina constantes for k in lista_exp: if not(k.has(s)): # es constante lista_exp.remove(k) # separados por lista_exp separados = sym.collect(Fs_0,lista_exp,evaluate=False) # factores por lista_exp Fs_fc = 0 for k in separados: Fs_k = sym.factor(separados[k],s) Fs_fc = Fs_fc + k*Fs_k return(Fs_fc) Fs_fp = apart_s(Fs) Fs_fc = factor_exp(Fs) # SALIDA print('\n F(s): ') sym.pprint(Fs) print('\n H(s) como fracciones parciales ') sym.pprint(Fs_fp) print('\n H(s) como factores de polos y ceros ') sym.pprint(Fs_fc)