Referencia: Lathi 4.3-3 p371, Lathi 2.4-2 p198
En un sistema acotado (bounded) estable, sometido a una señal de entrada en la que se conoce que su salida siempre es la misma, se lo considera un sistema BIBO-estable. (Bounded input, Boundes output)
La función de transferencia H(s) de un sistema es una descripción externa con la forma:
H(s) = \frac{P(s)}{Q(s)}El polinomio Q(s) representa una descripción interna, en la que si todos los polos de H(s) se encuentran en la parte izquierda del plano (left half plane, LHP), todos los términos h(t) son exponenciales decrecientes y h(t) es absolutamente integrable. En consecuencia el sistema es BIBO-estable.
Se asume que H(s) es una función en la que M ≤ N, siendo M el grado de P(s) y N e grado de Q(s), caso contrario el sistema es es BIBO-inestable.
1. Un sistema LTI CT es asintóticamente estable si y solo si todos los polos de su función de transferencia H(s) se encuentran en el lado izquierdo del plano, pudiendo ser simples o repetidos.
2. Un sistema LTI CT es inestable si y solo si se dan una o ambas de las condiciones:
2.1 Existe al menos un polo de H(s) en el lado derecho del plano RHP.
2.2 Existen polos repetidos de H(s) en el eje imaginario.
3. Un sistema LTI CT es marginalmente estable si y solo si, no hay polos de H(s) en el lado derecho del plano RHP y algunos polos NO repetidos sobre en el eje imaginario (parte Real = 0).
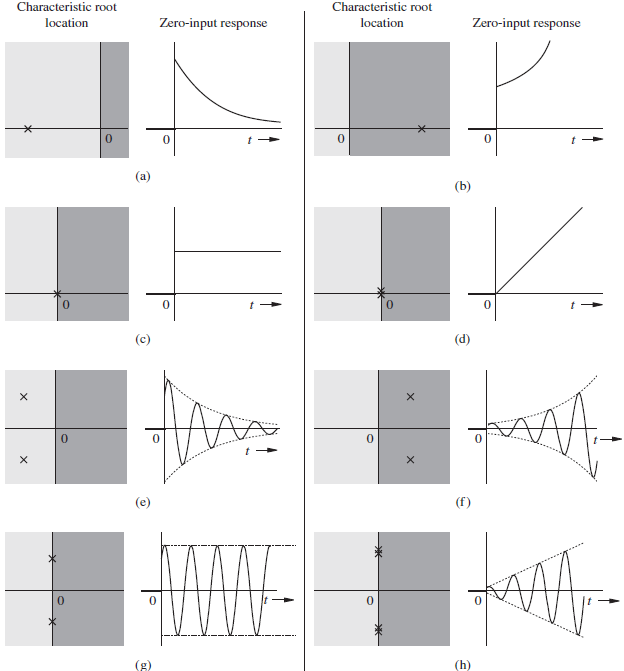
polos: [ no repetidos con RHP=0] [ no repetidos con RHP>=1 ] [ complejos sobre eje Imag únicos ] [ complejos sobre eje Imag repetidos ] [ H(s) con exponencial ]
..
Ejemplo 1. H(s) con polos no repetidos, RHP=0
Referencia: Lathi 2.14a p201
Revise la estabilidad BIBO de los siguientes sistemas LTI¨CT descritos por las ecuaciones:
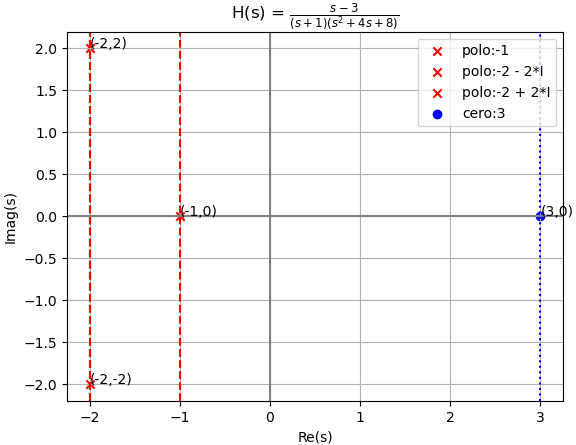
(D+1)(D^2 + 4D +8) y(t) = (D-3) x(t)Ejemplo 1 Desarrollo analítico
Se expresa la ecuación de operadores diferenciales D por la transformada de Laplace.
(s+1)(s^2 + 4s +8) Y(s) = (s-3) X(s) \frac{Y(s)}{X(s)} = \frac{s-3}{(s+1)(s^2 + 4s +8)}El grado del polinomio Q es N=3 y es mayor que el grado del polinomio P es M=1.
La expresión de entrada se escribe en el algoritmo como:
Hs = ((s-3)/(s+1))*(1/(s**2+4*s+8))
Los polos se obtienen como las raíces del denominador Q, necesario para plantear las fracciones parciales y simplificar la expresión como la suma de componentes más simples.
polos: {-1: 1, -2 - 2*I: 1, -2 + 2*I: 1}
Las fracciones parciales de H(s) usando el algoritmo de la sección anterior se obtiene
H(s) = \frac{1}{5}\frac{4}{s+1}+\frac{1}{5} \frac{4s+17}{s^2 + 4s +8}Ejemplo 1 Desarrollo con Sympy-Python
Con el algoritmo se tiene el siguiente resultado:
busca_PolosCeros:
Q_polos : {-1: 1, -2 - 2*I: 1, -2 + 2*I: 1}
P_ceros : {3: 1}
polos reales: 1
polos complejos: 2
sobre lado derecho RHP: 0
sobre Eje Imaginario, repetidos: 0 unicos: 0
asintoticamente: estable
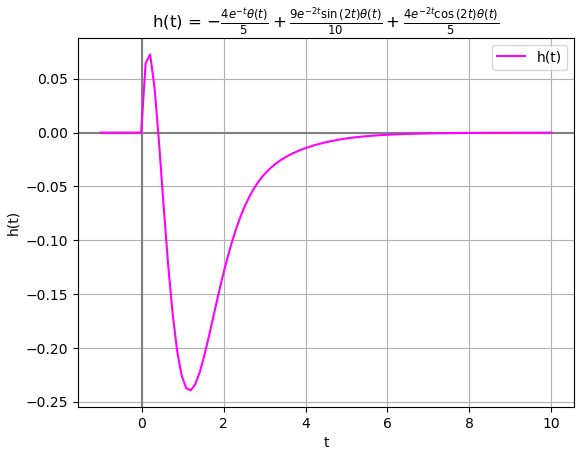
h(t):
-t -2*t -2*t
4*e *Heaviside(t) 9*e *sin(2*t)*Heaviside(t) 4*e *cos(2*t)*Heaviside(t)
- ------------------ + ----------------------------- + -----------------------------
5 10 5
>>>
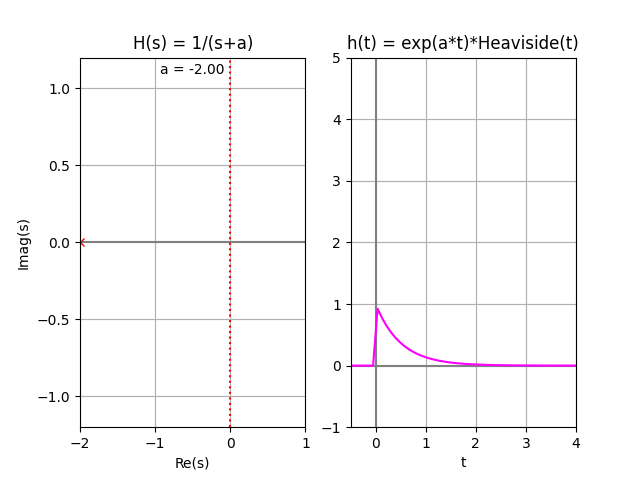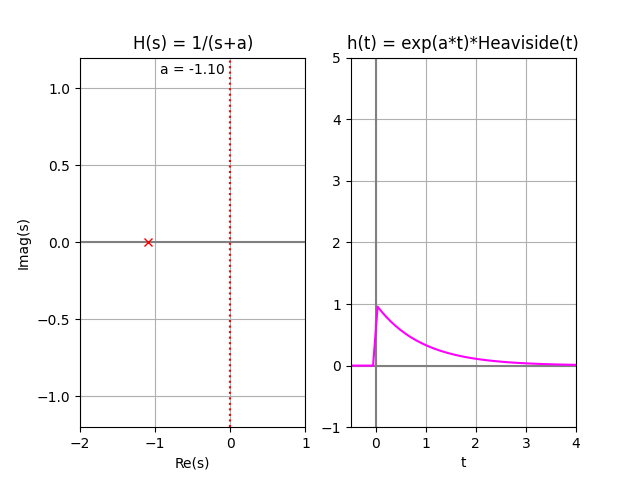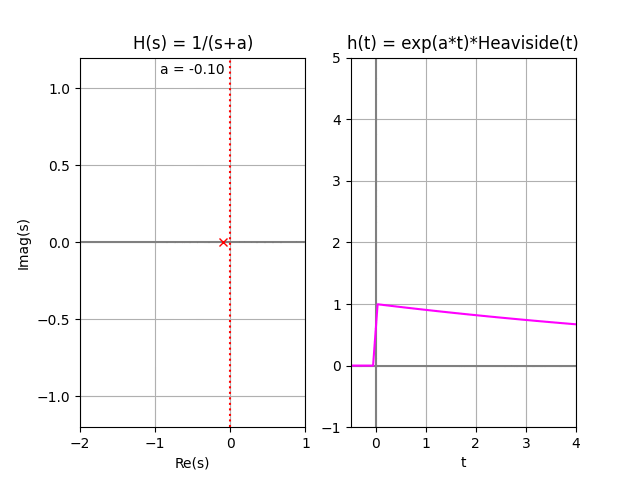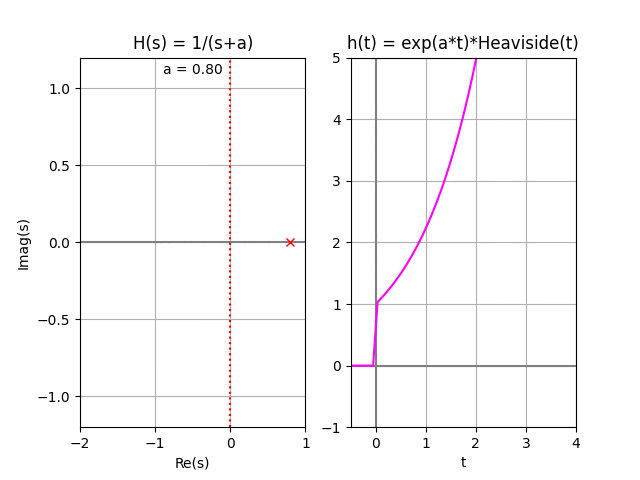
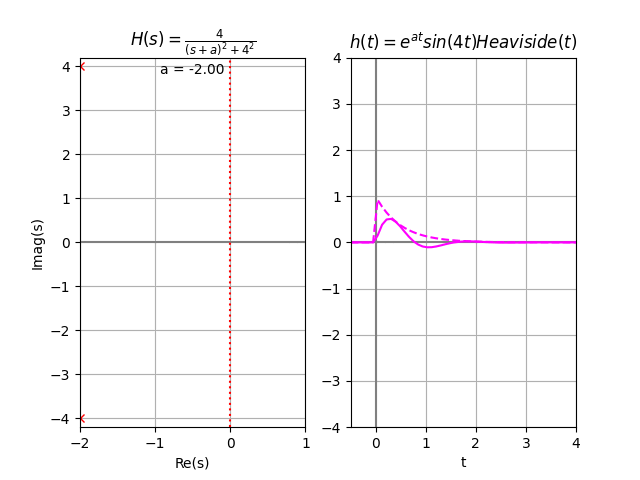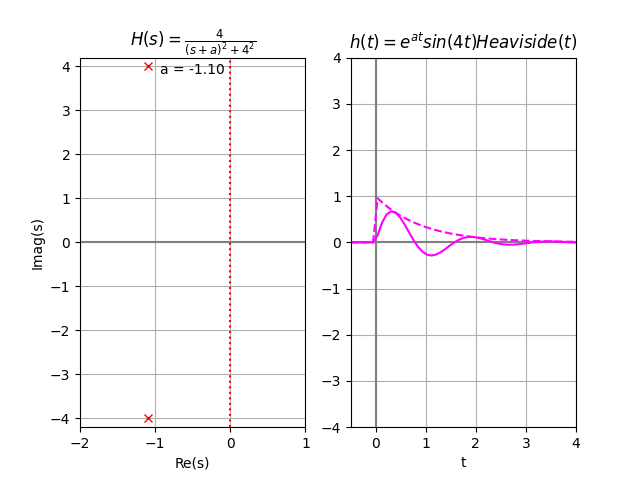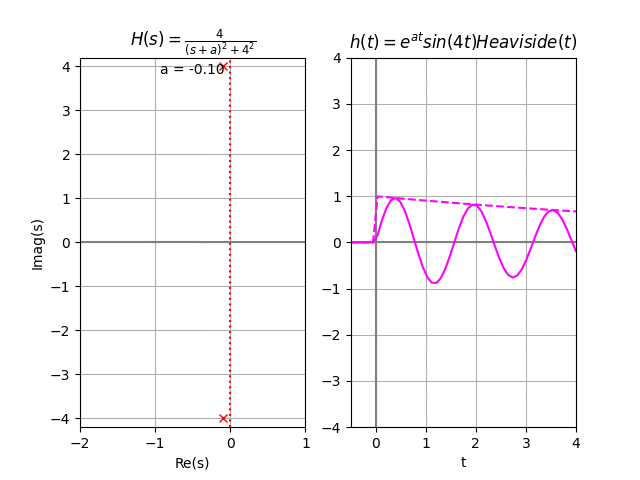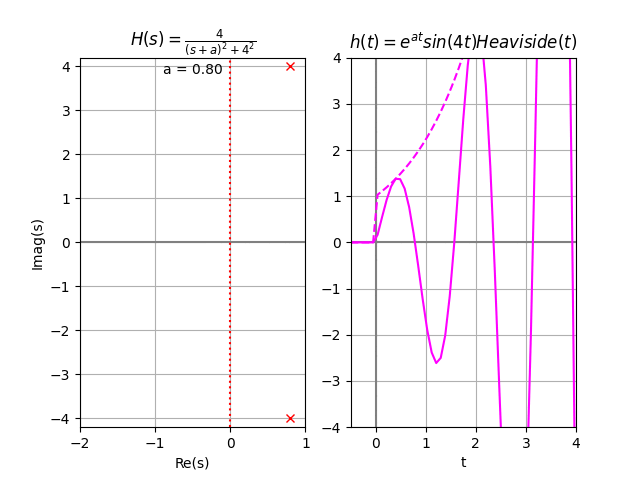
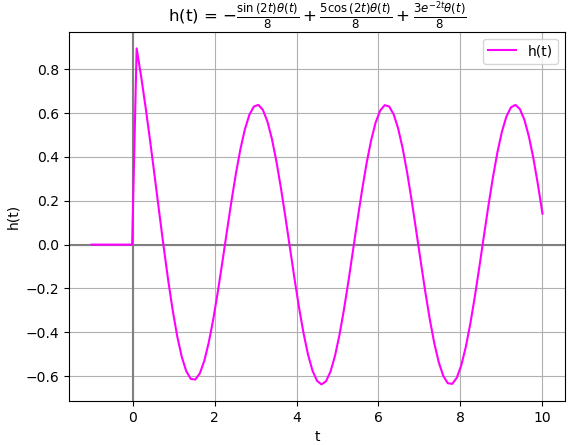
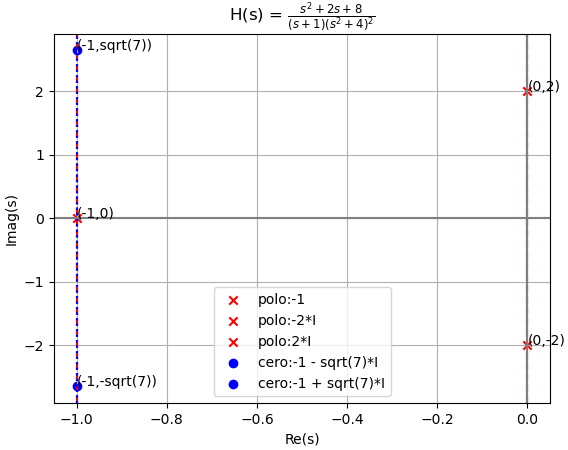
En la gráfica se observa que todos los polos se encuentran en el lado izquierdo del plano LHP. Por lo que se considera que existen asintotas en la función correspondiente a tiempo, y el sistema es «asintóticamente estable«. También se considera BIBO estable por no tener los polos en el lado derecho RHP=0
la gráfica de h(t) muestra lo indicado por el análisis de polos
Instrucciones en Python Ejemplo 1
El algoritmo es una continuación del manejo de Polos y Ceros realizado en la sección anterior, donde se añade la revisión de las raíces de Q cuando son de tipo imaginarias.
Por simplicidad para el análisis se usan solo las partes esenciales, asi el enfoque es sobre la posición de los polos y su relación con h(t).
En el proceso, se agrupan las partes reales en Q_real y las imaginaria en Q_imag para realizar el conteo de lo repetido.
# Polos y ceros de funcion de transferencia H(s) # Estabilidad del sistema, H(s) respuesta al impulso # Ps es numerador, Qs es denominador import numpy as np import sympy as sym import matplotlib.pyplot as plt import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t',real=True) Hs = ((s-3)/(s+1))*(1/(s**2+4*s+8)) # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 10 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO polosceros = fcnm.busca_polosceros(Hs) P_ceros = polosceros['P_ceros'] Q_polos = polosceros['Q_polos'] # h(t) desde H_fp(s) con inversa Laplace ht = sym.inverse_laplace_transform(Hs,s,t) # SALIDA # Analiza estabilidad asintotica casi_cero = 1e-12 # Separa parte real e imaginaria de raices cuenta_real = 0; cuenta_imag = 0 unicos = 0 ; repetidos = 0 ; enRHP = 0 for raiz in Q_polos: [r_real,r_imag] = raiz.as_real_imag() if abs(r_real)>casi_cero and abs(r_imag)<casi_cero : cuenta_real = cuenta_real+1 # para estabilidad asintotica conteo = Q_polos[raiz] if conteo==1 and r_real==0 and abs(r_imag)>0: unicos = unicos + 1 if conteo>1 and r_real==0 and abs(r_imag)>0: repetidos = repetidos + 1 if r_real>0: enRHP = enRHP + 1 cuenta_imag = len(Q_polos)-cuenta_real # Revisa lado derecho del plano RHP asintota = "" if enRHP==0: asintota = 'estable' if enRHP>0 or repetidos>0: asintota = 'inestable' if enRHP==0 and unicos>0: asintota = 'marginalmente estable' # SALIDA print('busca_PolosCeros:') for k in polosceros.keys(): eq_lista = ['H','H_fp'] if k in eq_lista: print('',k,':') sym.pprint(polosceros[k]) else: print('\n',k,':',polosceros[k]) print(' polos reales: ',cuenta_real) print(' polos complejos: ',cuenta_imag) print(' sobre lado derecho RHP:',enRHP) print(' sobre Eje Imaginario, repetidos: ', repetidos,' unicos:', unicos) print('\n asintoticamente: ', asintota) print('\n h(t): ') sym.pprint(ht) # GRAFICA ----------- muestras_H = 161 fig_Hs = fcnm.graficar_Fs(Hs,Q_polos,P_ceros, muestras=muestras_H, f_nombre='H', solopolos=True) figura_h = fcnm.graficar_ft(ht,t_a,t_b,f_nombre='h') plt.show()
polos: [ no repetidos con RHP=0] [ no repetidos con RHP>=1 ] [ complejos sobre eje Imag únicos ] [ complejos sobre eje Imag repetidos ] [ H(s) con exponencial ]
..
Ejemplo 2 H(s) con polos no repetidos, uno en RHP
Referencia: Lathi 2.14b p201
Revise la estabilidad BIBO de los siguientes sistemas LTIC descritos por las ecuaciones:
(D-1)(D^2 + 4D +8) y(t) = (D+2) x(t)Ejemplo 2 Desarrollo analítico
Se expresa la ecuación de operadores diferenciales D por la transformada de Laplace.
(s-1)(s^2 + 4s +8) Y(s) = (s+2) X(s) \frac{Y(s)}{X(s)} = \frac{s+2}{(s-1)(s^2 + 4s +8)}El grado del polinomio Q es N=3 y es mayor que el grado del polinomio P es M=1.
Los polos se obtienen como las raíces del denominador Q, necesario para plantear las fracciones parciales y simplificar la expresión en componentes más simples.
La expresión para el algoritmo se escribe como:
Hs = ((s+2)/(s-1))*(1/(s**2+4*s+8))
y el resultado de polos obtenido es:
polos: {1: 1, -2 - 2*I: 1, -2 + 2*I: 1}
Las fracciones parciales de H(s) usando el algoritmo de la sección anterior se obtiene
H(s) = \frac{3}{13}\frac{1}{s-1}+\frac{1}{13} \frac{3s+2}{s^2 + 4s +8}Ejemplo 2 Desarrollo con Sympy-Python
Con el algoritmo se tiene el siguiente resultado:
busca_PolosCeros:
H :
s + 2
----------------------
/ 2 \
(s - 1)*\s + 4*s + 8/
H_fp :
3*s + 2 3
- ----------------- + ----------
/ 2 \ 13*(s - 1)
13*\s + 4*s + 8/
P_ceros : {-2: 1}
Q_polos : {1: 1, -2 - 2*I: 1, -2 + 2*I: 1}
polos reales: 1
polos complejos: 2
sobre lado derecho RHP: 1
sobre Eje Imaginario, repetidos: 0 unicos: 0
asintoticamente: inestable
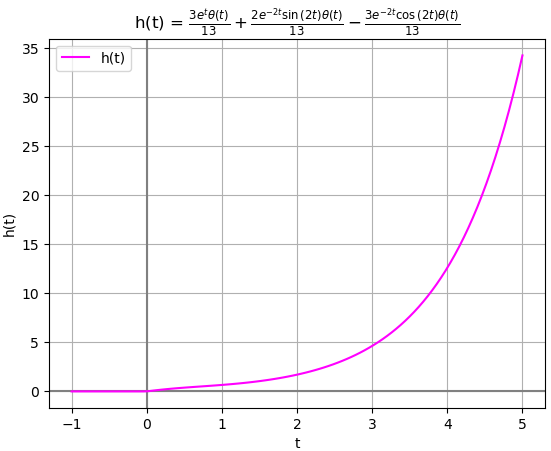
h(t):
t -2*t -2*t
3*e *Heaviside(t) 2*e *sin(2*t)*Heaviside(t) 3*e *cos(2*t)*Heaviside(t)
----------------- + ----------------------------- - -----------------------------
13 13 13
>>>
En la gráfica se observa que un polo se encuentra en el lado derecho del plano RHP. Un polo en RHP genera un componente creciente en el tiempo, en consecuencia, el sistema es «asintóticamente inestable». También el sistema es BIBO inestable.
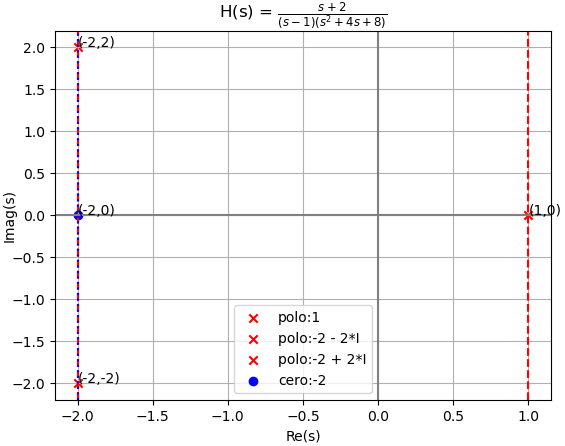
la gráfica de h(t) complementa lo interpretado con la posición de los polos en el plano s
polos: [ no repetidos con RHP=0] [ no repetidos con RHP>=1 ] [ complejos sobre eje Imag únicos ] [ complejos sobre eje Imag repetidos ] [ H(s) con exponencial ]
Ejemplo 3 H(s) con polos complejos sobre eje imaginario únicos
Referencia: Lathi 2.14c p201
Revise la estabilidad BIBO de los siguientes sistemas LTIC descritos por las ecuaciones:
(D+2)(D^2 +4)y(t) = (D^2+D+1)x(t)Se expresa la ecuación de operadores diferenciales D por la transformada de Laplace.
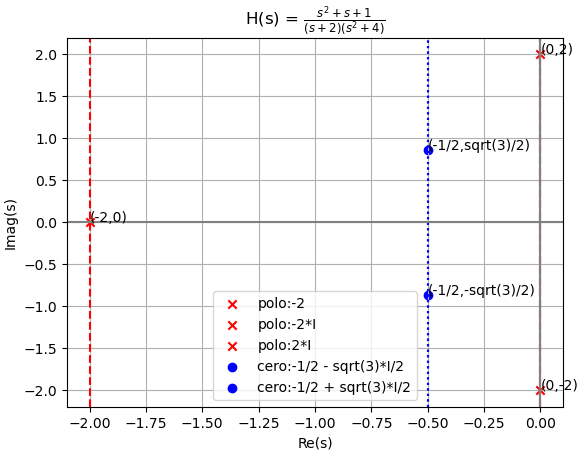
(s+2)(s^2 + 4) Y(s) = (s^2+s+1) X(s)Ps = s**2+s+1 Qs = (s+2)*(s**2+4) Hs = Ps/Qs
El grado del polinomio Q es N=3 y el grado del polinomo P es M=2, los polos del denominador muestran raíces complejas, por lo que se tendrá componentes cuadráticos para la transformada inversa de Laplace.
Q_polos : {-2: 1, -2*I: 1, 2*I: 1}
Usando fracciones parciales con el algoritmo se tiene que,
H(s) = \frac{3}{8}\frac{1}{s+2}+\frac{1}{8} \frac{5s-2}{s^2 + 4}resultados:
busca_PolosCeros:
Q_polos : {-2: 1, -2*I: 1, 2*I: 1}
P_ceros : {-1/2 - sqrt(3)*I/2: 1, -1/2 + sqrt(3)*I/2: 1}
polos reales: 1
polos complejos: 2
sobre lado derecho RHP: 0
sobre Eje Imaginario, repetidos: 0 unicos: 2
asintoticamente: marginalmente estable
h(t):
-2*t
sin(2*t)*Heaviside(t) 5*cos(2*t)*Heaviside(t) 3*e *Heaviside(t)
- --------------------- + ----------------------- + --------------------
8 8 8
>>>
al tener polos sobre el eje imaginario el sistema es asintóticamente marginal estable, pero BIBO-inestable.
con gráfica de h(t)
polos: [ no repetidos con RHP=0] [ no repetidos con RHP>=1 ] [ complejos sobre eje Imag únicos ] [ complejos sobre eje Imag repetidos ] [ H(s) con exponencial ]
…
Ejemplo 4. H(s) con polos repetidos sobre eje imaginario
Referencia: Lathi 2.14d p201
Revise la estabilidad BIBO de los siguientes sistemas LTIC descritos por las ecuaciones:
(D+1)(D^2 + 4)^2 y(t) = (D^2 + 2D + 8) x(t)Se expresa la ecuación de operadores diferenciales D por la transformada de Laplace.
(s+1)(s^2 + 4)^2 Y(s) = (s^2 + 2s + 8) X(s)Las raíces del denominador Q muestran que tienen valores complejos, mostrando que se usaría un componente cuadratico para la transformada inversa de Laplace.
polos: {-1: 1, -2*I: 2, 2*I: 2}
al presentar dos raíces repetidas sobre el eje imaginario, se considera asintóticamente inestable y también BIBO inestable.
Revise el resultado de la inversa de Laplace usando las tablas.
los resultados con el algoritmo son:
busca_PolosCeros:
H :
2
s + 2*s + 8
-----------------
2
/ 2 \
(s + 1)*\s + 4/
H_fp :
2*(s - 6) 7*(s - 1) 7
- ----------- - ----------- + ----------
2 / 2 \ 25*(s + 1)
/ 2 \ 25*\s + 4/
5*\s + 4/
P_ceros : {-1 - sqrt(7)*I: 1, -1 + sqrt(7)*I: 1}
Q_polos : {-1: 1, -2*I: 2, 2*I: 2}
polos reales: 1
polos complejos: 2
sobre lado derecho RHP: 0
sobre Eje Imaginario, repetidos: 2 unicos: 0
asintoticamente: inestable
>>>
gráfica de polos
polos: [ no repetidos con RHP=0] [ no repetidos con RHP>=1 ] [ complejos sobre eje Imag únicos ] [ complejos sobre eje Imag repetidos ] [ H(s) con exponencial ]
Tarea
Lathi ejercicios 2.15 p202
Ejemplo 5. Con suma de términos y exponenciales de retraso en tiempo
H(s) = \frac{s+2}{s-1}+ \frac{e^{-2s}}{s-2}la expresión para el algoritmo se escribe como:
Hs = (s+2)/(s-1) + sym.exp(-2*s)/(s-2)
con lo que se obtiene el resultado, usando intervalo de tiempo [-1,3] para las gráficas.
exp(-2*s) : {'Q_polos': {2: 1}, 'P_ceros': {}, 'Hs_k': 1/(s - 2)}
1 : {'Q_polos': {1: 1}, 'P_ceros': {-2: 1}, 'Hs_k': (s + 2)/(s - 1)}
Q_polos : {2: 1, 1: 1}
P_ceros : {-2: 1}
n_polos_real : 2
n_polos_imag : 0
enRHP : 2
unicos : 0
repetidos : 0
asintota : inestable
h(t):
-4 2*t t
e *e *Heaviside(t - 2) + 3*e *Heaviside(t) + DiracDelta(t)
>>>
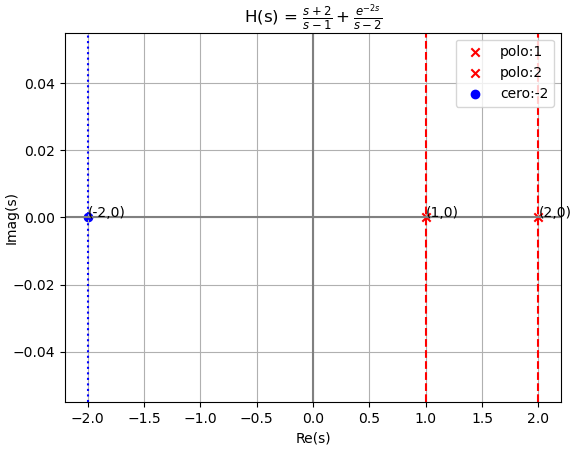
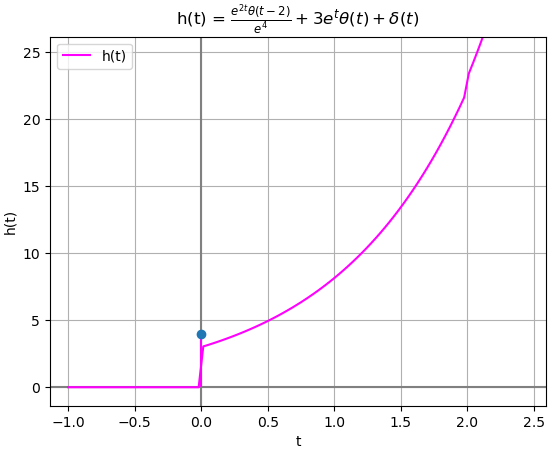
con gráfica de polos
con gráfica h(t)
Instrucciones con Python
# Estabilidad del sistema, H(s) respuesta al impulso # Polos y ceros de funcion de transferencia H(s) # Ps es numerador, Qs es denominador import sympy as sym import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t',real=True) Hs = (s+2)/(s-1) + sym.exp(-2*s)/(s-2) # Ps = s**2+2*s+8 # Qs = (s+1)*((s**2+4)**2) # Hs = Ps/Qs #Ps = s**2+s+1 #Qs = (s+2)*(s**2+4) #Hs = Ps/Qs #Hs = ((s+2)/(s-1))*(1/(s**2+4*s+8)) #Hs = ((s-3)/(s+1))*(1/(s**2+4*s+8)) # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 10 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO Hs_fp = fcnm.apart_s(Hs) polosceros = fcnm.busca_polosceros(Hs_fp) P_ceros = polosceros['P_ceros'] Q_polos = polosceros['Q_polos'] def estabilidad_asintotica_s(Q_polos, casi_cero=1e-8): ''' Analiza estabilidad asintotica con Q_raiz Separa parte real e imaginaria de raices casicero es la tolerancia para considerar cero ''' # Separa parte real e imaginaria de raices cuenta_real = 0; cuenta_imag = 0 unicos = 0 ; repetidos = 0 ; enRHP = 0 for raiz in Q_polos: [r_real,r_imag] = raiz.as_real_imag() if abs(r_real)>casi_cero and abs(r_imag)<casi_cero : cuenta_real = cuenta_real+1 # para estabilidad asintotica conteo = Q_polos[raiz] if conteo==1 and r_real==0 and abs(r_imag)>0: unicos = unicos + 1 if conteo>1 and r_real==0 and abs(r_imag)>0: repetidos = repetidos + 1 if r_real>0: enRHP = enRHP + 1 cuenta_imag = len(Q_polos)-cuenta_real # Revisa lado derecho del plano RHP asintota = "" if enRHP==0: asintota = 'estable' if enRHP>0 or repetidos>0: asintota = 'inestable' if enRHP==0 and unicos>0: asintota = 'marginalmente estable' estable = {'n_polos_real': cuenta_real, 'n_polos_imag': cuenta_imag, 'enRHP' : enRHP, 'unicos' : unicos, 'repetidos' : repetidos, 'asintota' : asintota,} return(estable) estable = estabilidad_asintotica_s(Q_polos) # h(t) desde H_fp(s) con inversa Laplace ht = 0*t term_suma = sym.Add.make_args(Hs_fp.expand()) for term_k in term_suma: ht_k = sym.inverse_laplace_transform(term_k,s,t) ht = ht +ht_k ht = sym.expand(ht,t) # terminos suma # SALIDA fcnm.print_resultado_dict(polosceros) fcnm.print_resultado_dict(estable) print('\n h(t): ') sym.pprint(ht) # GRAFICA ----------- import matplotlib.pyplot as plt muestras_H = 161 fig_Hs = fcnm.graficar_Fs(Hs_fp,Q_polos,P_ceros, muestras=muestras_H, f_nombre='H',solopolos=True) figura_h = fcnm.graficar_ft(ht,t_a,t_b,f_nombre='h') plt.show()
polos: [ no repetidos con RHP=0] [ no repetidos con RHP>=1 ] [ complejos sobre eje Imag únicos ] [ complejos sobre eje Imag repetidos ] [ H(s) con exponencial ]
H(s) Implicaciones de estabilidad y Osciladores
Referencia: Lathi 2.5-3 p203
Todos los sistemas de procesamiento de señales deben ser asintóticamente estables.
Los sistemas inestables no son requeridos debido a que con condiciones iniciales, intencionales o no, llevan a respuestas fuera de rango. Estas respuestas inestables destruyen el sistema o lo llevan a condiciones de saturación que cambian la naturaleza del sistema debido al tipo de crecimiento exponencial.
Sistemas marginalmente estables, aunque BIBO inestables, tienen aplicación como osciladores, que es un sistema que genera su propia señal sin la aplicación de entradas externas.
La salida de un oscilador es una respuesta de entrada cero. Si la respuesta es una sinusiode con frecuencia ω0 el sistema es marginalmente estable en ±jω0. Para diseñar un oscilador de frecuencia se debe usar un sistema descrito por la ecuación diferencial:
(D^2 + \omega _0 ^2 ) y(t) = x(t)Sin embargo, osciladores en la práctica se construyen con sistemas no lineales.