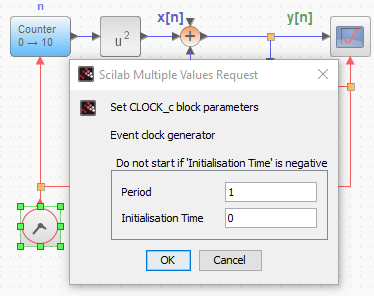
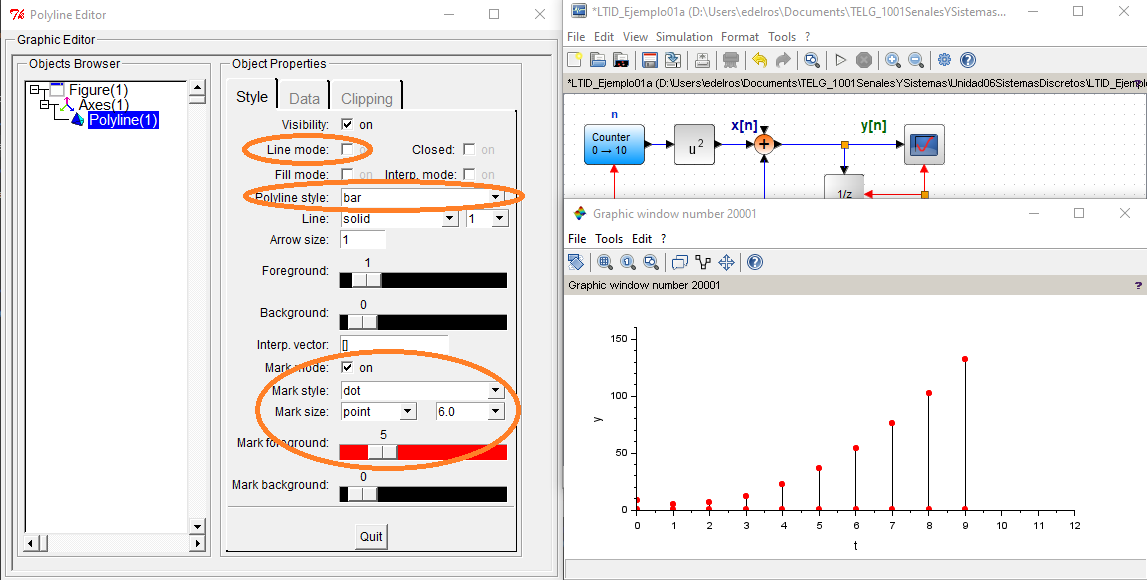
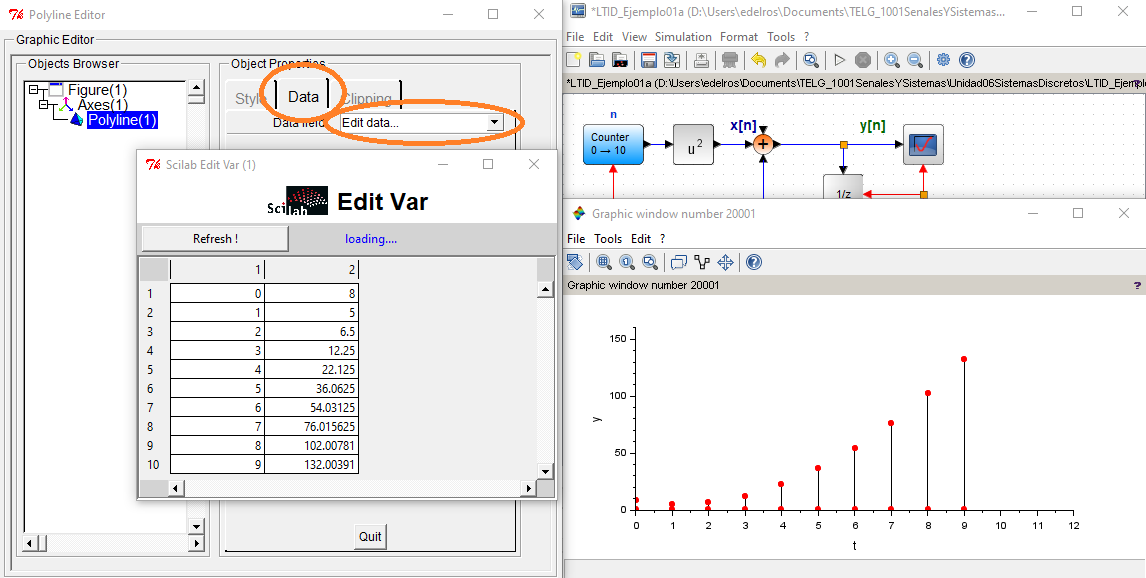
El ejercicio planteado en Sistema Discreto – Solución iterativa, se desarrolla con un algoritmo en Python.
Ejercicio 1
Referencia: Lathi ejemplo 3.11 p266
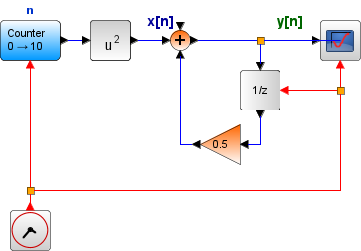
Un sistema LTID tiene la siguiente expresión:
y[n] - 0.5 y[n-1] = x[n]
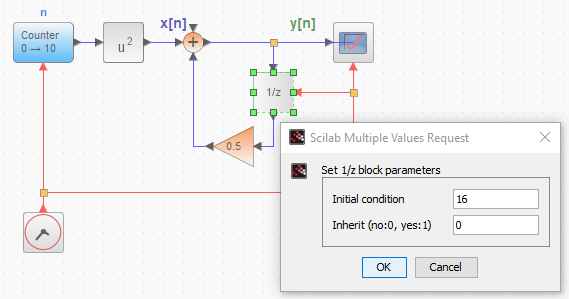
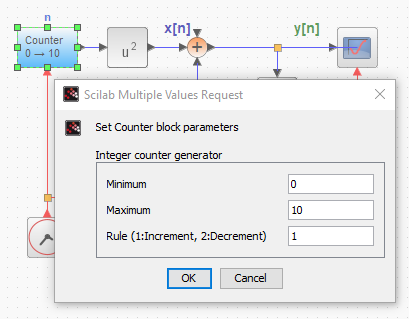
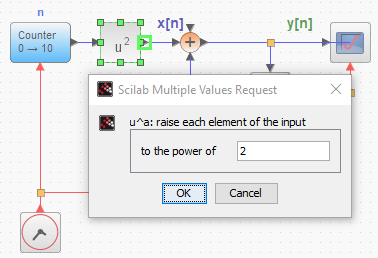
con condiciones iniciales y[-1]=16 y entrada causal x[n] = n2 ,para n≥0.
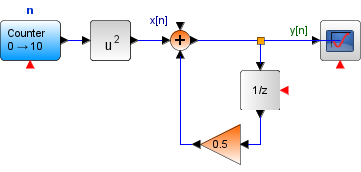
El algoritmo tiene el siguiente resultado:

muestras: 10
[[ n, xi, yi]]
[[ -1. 0. 16. ]
[ 0. 0. 8. ]
[ 1. 1. 5. ]
[ 2. 4. 6.5 ]
[ 3. 9. 12.25]
[ 4. 16. 22.12]
[ 5. 25. 36.06]
[ 6. 36. 54.03]
[ 7. 49. 76.02]
[ 8. 64. 102.01]
[ 9. 81. 132. ]]
>>>
Algoritmo en Python
Las condiciones iniciales se ingresan como un vector con valores de posición ascendente. También es necesario indicar el número de muestras a observar. esto permite construir el vector de salida yi.
Las fórmulas de entrada y salida se muestran en la sección «calcula los siguientes valores»
# Sistema LTID. Solución iterativa
# Ejercicio Lathi ejemplo 3.11 p266
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
muestras = 10
# condiciones iniciales ascendente ...,y[-2],y[-1]
y0 = [16.]
# PROCEDIMIENTO
m0 = len(y0)
m = muestras + m0
# vectores
n = np.arange(-m0,muestras,1)
xi = np.zeros(m, dtype=float)
yi = np.zeros(m, dtype=float)
# añade condiciones iniciales
xi[0:m0] = 0
yi[0:m0] = y0
# calcula los siguientes valores
for k in range(m0,m,1):
xi[k] = n[k]**2
yi[k] = 0.5*yi[k-1]+xi[k]
# tabla de valores
tabla = np.concatenate([[n],[xi],[yi]], axis=0)
tabla = np.transpose(tabla)
# SALIDA
np.set_printoptions(precision=2)
print('muestras: ', muestras)
print('[[ n, xi, yi]]')
print(tabla)
# Gráfica
plt.subplot(211)
plt.stem(n,xi,label='x[n]=n**2')
plt.xlabel('n')
plt.ylabel('x[n]')
plt.axvline(0,color='gray')
plt.legend()
plt.grid()
plt.subplot(212)
plt.stem(n,yi,label='y[n]=0.5y[n-1]+x[n]',
markerfmt='go',
linefmt='green')
plt.xlabel('n')
plt.ylabel('y[n]')
plt.axvline(0,color='gray')
plt.legend()
plt.grid()
plt.show()
Ejercicio 2
Se aplica el mismo algoritmo a otro ejercicio para comparar resultados con lo realizado en forma analítica.
Referencia: Lathi ejemplo 3.12 p267
Resolver de forma iterativa,
y[n+2] - y[n+1] +0.24y[n] = x[n+2] - 2x[n+1]
con las condiciones iniciales de y[-1] = 2, y[-2] =1 y entrada causal x[n]=n que inicia en n=0
Para usar la ecuación en el algoritmo, se desplaza dos posiciones en ambos lados de la ecuacion para despejar y[n]
y[n] - y[n-1] +0.24y[n-2] = x[n0] - 2x[n-1]
y[n] = y[n-1] -0.24y[n-2] + x[n0] - 2x[n-1]
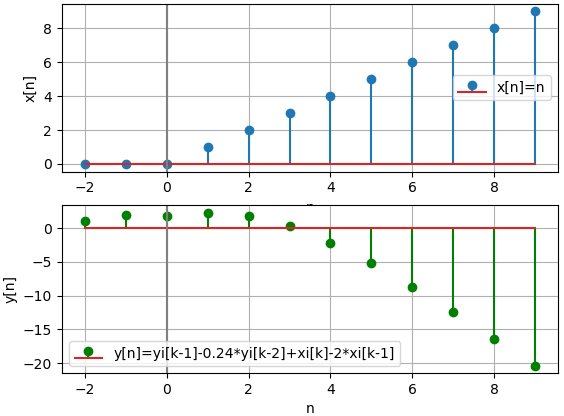
muestras: 10
[[ n, xi, yi]]
[[ -2. 0. 1. ]
[ -1. 0. 2. ]
[ 0. 0. 1.76]
[ 1. 1. 2.28]
[ 2. 2. 1.86]
[ 3. 3. 0.31]
[ 4. 4. -2.14]
[ 5. 5. -5.21]
[ 6. 6. -8.7 ]
[ 7. 7. -12.45]
[ 8. 8. -16.36]
[ 9. 9. -20.37]]
>>>
Algoritmo en Python
# Sistema LTID. Solución iterativa
# Ejercicio Lathi ejemplo 3.12 p267
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
muestras = 10
# condiciones iniciales ascendente ...,y[-2],y[-1]
y0 = [1,2]
# PROCEDIMIENTO
m0 = len(y0)
m = muestras + m0
# vectores
n = np.arange(-m0,muestras,1)
xi = np.zeros(m, dtype=float)
yi = np.zeros(m, dtype=float)
# añade condiciones iniciales
xi[0:m0] = 0
yi[0:m0] = y0
# calcula los siguientes valores
for k in range(m0,m,1):
xi[k] = n[k]
yi[k] = yi[k-1]-0.24*yi[k-2]+xi[k]-2*xi[k-1]
# tabla de valores
tabla = np.concatenate([[n],[xi],[yi]], axis=0)
tabla = np.transpose(tabla)
# SALIDA
np.set_printoptions(precision=2)
print('muestras: ', muestras)
print('[[ n, xi, yi]]')
print(tabla)
# Gráfica
plt.subplot(211)
plt.stem(n,xi,label='x[n]=n')
plt.xlabel('n')
plt.ylabel('x[n]')
plt.axvline(0,color='gray')
plt.legend()
plt.grid()
plt.subplot(212)
plt.stem(n,yi,label='y[n]=yi[k-1]-0.24*yi[k-2]+xi[k]-2*xi[k-1]',
markerfmt='go',
linefmt='green')
plt.xlabel('n')
plt.ylabel('y[n]')
plt.axvline(0,color='gray')
plt.legend()
plt.grid()
plt.show()