Referencia: Lathi 4.4-1 p382, Oppenheim 11.50 p896
Se amplian los conceptos de circuitos pasivos analizados con transformadas e Laplace, aplicando a circuitos activos. Se obtienen los circuitos equivalentes o modelos matemáticos y se repiten los procedimientos anteriores.
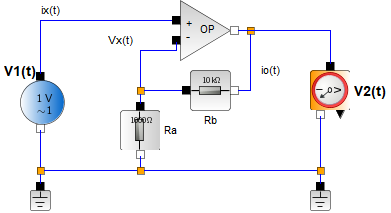
El elemento activo más conocido es el amplificador operacional (op amp) que tienen ganancia "muy alta". El voltaje de salida v2 = - A v1, donde A es del orden de 105 o 106. Un factor importante es que la impedancia de entrada es muy alta del orden de 1012Ω y la impedancia de salida es muy baja (50-100Ω)
La configuración de la ganancia se establece con los resistores Ra y Rb y la forma de conectar las entradas y salidas.
K = 1+\frac{R_a}{R_b} v_2 = K v_1 v_2 = (R_b + R_a) i_o = R_b i_o + R_a i_o v_2 = v_s = Ra i_o = R_a i_o \frac{v_2}{v_1} =\frac{R_b+R_a}{R_a} = 1+\frac{R_b}{R_a} = K1. Amplificador Operacional en el dominio s
Referencia: Lathi 4.6-5 p399
Dada la alta impedancia del op amp, la corriente de retroalimentación I(s) fluye solo por los resistores. El voltaje de entrada es cero o muy pequeño dada la ganancia muy grande del op amp. Dadas estas simplificaciones, se aproxima con mucha precisión que:
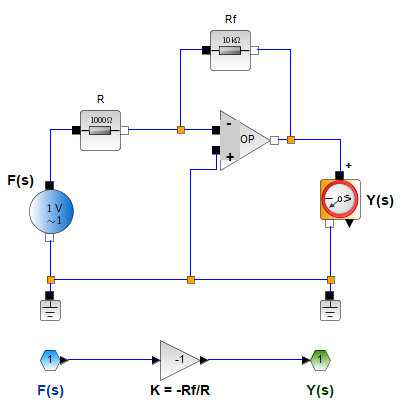
Y(s) = - I(s) Z_f(s) I(s) = \frac{X(s)}{Z(s)} Y(s) = -\frac{Z_f(s)}{Z(s)} H(s) = -\frac{Z_f(s)}{Z(s)}1,1 Amplificador Operacional como multiplicador escalar
H(s) = -\frac{R_f}{R}1,2 Amplificador Operacional como Integrador
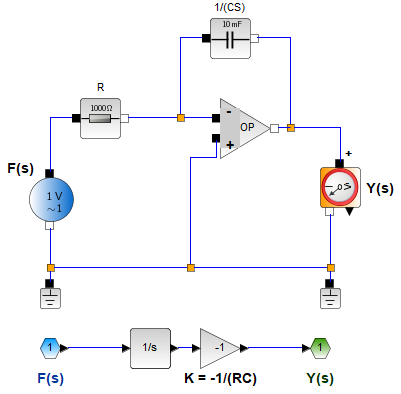
Referencia: Oppenheim 11.52 p898
H(s) = \Big(-\frac{1}{RC}\Big) \frac{1}{s}1,3 Amplificador Operacional como Sumador
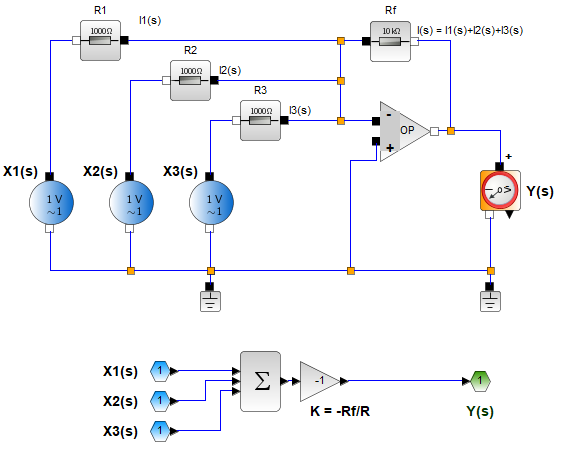
Y(s) = - \Big[\frac{R_f}{R_1}X_1(s)+\frac{R_f}{R_2}X_2(s)+\frac{R_f}{R_3}X_3(s) \Big]Observe que las ganancias del sumador son siempre negativas, hay una inversión de signo en cada señal de entrada.
Y(s) = K_1 X_1(s)+K_2 X_2(s)+K_3 X_3(s)Ejemplo 1. Implementación con Op-Amp
Referencia: Lathi 4.25 p401
Realizar la implementación de un sistema dado por la función de transferencia H(s)
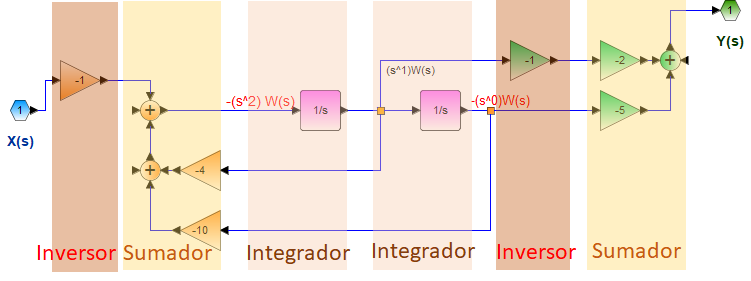
H(s) = \frac{2s+5}{s^2+4s+10}El diagrama de bloques de la función de transferencia H(s) es,
Se agrupan algunos elementos como sumadores y sus factores de multiplicación. Para referencia se etiqueta cada punto como señal W(s) en cada punto donde el orden del exponente de 's' es diferente.
Se considera la inversión de signo de la señal de entrada por la configuración del amplificador operacional y el factor K de cada rama a usar.
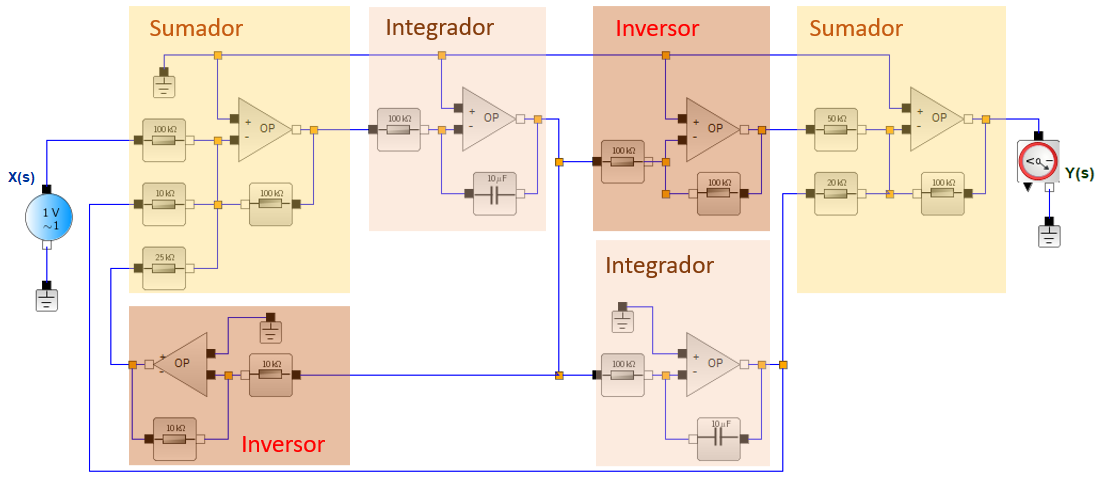
Se identifica el tipo de op amp a usar y se establecen los valores de los resistores en múltiplos de 10KΩ y los capacitores en el orden de 10 μF.
Ejemplo 1. Desarrollo analítico
Para revisar el comportamiento del circuito, en caso de implementarlo con OpAmps, el resultado de la función de transferencia para el impulso usando el algoritmo de la sección LTI CT Laplace – Ejercicio resuelto para Y(s)=H(s)X(s) con Sympy-Python
H(s) = P(s)/Q(s):
2*s + 5
-------------
2
s + 4*s + 10
H(s) en factores:
2*s + 5
-------------
2
s + 4*s + 10
H(s) parámetros cuadraticos:
(2*s + 5)/(s**2 + 4*s + 10) :
{'A': 2.0, 'B': 5.0, 'a': 2.0, 'c': 10.0,
'r': 2.041241452319315, 'b': 2.449489742783178,
'theta': -0.20135792079033082}
h(t) :
/ ___ -2*t / ___ \ \
|\/ 6 *e *sin\\/ 6 *t/ -2*t / ___ \|
|------------------------ + 2*e *cos\\/ 6 *t/|*Heaviside(t)
\ 6 /
polosceros:
Q_polos : {-2 - sqrt(6)*I: 1, -2 + sqrt(6)*I: 1}
P_ceros : {-5/2: 1}
Estabilidad de H(s):
n_polos_real : 0
n_polos_imag : 2
enRHP : 0
unicos : 0
repetidos : 0
asintota : estable
X(s):
1
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0
ZSR respuesta estado cero:
ZSR :
2*s + 5
-------------
2
s + 4*s + 10
ZSR_Qs2 :
(2*s + 5)/(s**2 + 4*s + 10) :
{'A': 2.0, 'B': 5.0, 'a': 2.0, 'c': 10.0,
'r': 2.041241452319315, 'b': 2.449489742783178,
'theta': -0.20135792079033082}
yt_ZSR :
/ ___ -2*t / ___ \ \
|\/ 6 *e *sin\\/ 6 *t/ -2*t / ___ \|
|------------------------ + 2*e *cos\\/ 6 *t/|*Heaviside(t)
\ 6 /
Y(s)_total = ZIR + ZSR:
2*s + 5
-------------
2
s + 4*s + 10
y(t)_total = ZIR + ZSR:
/ ___ -2*t / ___ \ \
|\/ 6 *e *sin\\/ 6 *t/ -2*t / ___ \|
|------------------------ + 2*e *cos\\/ 6 *t/|*Heaviside(t)
\ 6 /
>>>
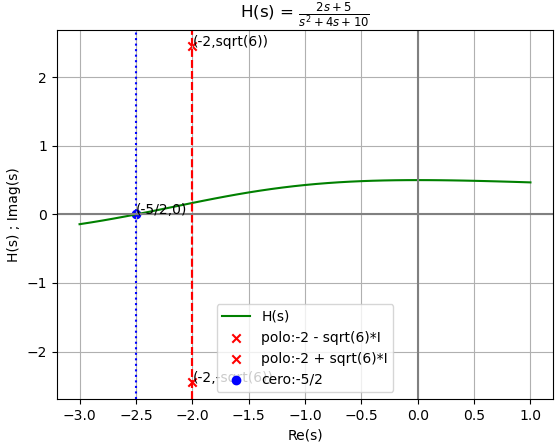
donde la gráfica de polos muestra que se encuentran todos del lado izquierdo del plano
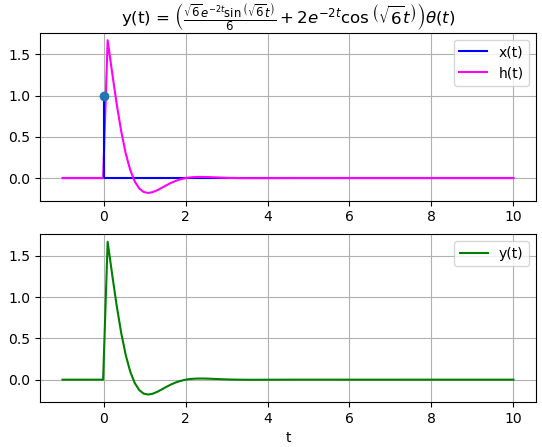
También se muestra la respuesta al impulso h(t) del circuito
Las respuestas fueron obtenidas al usar como bloque de entrada,
# H(s) respuesta impulso Ps = 2*s+5 Qs = s**2 + 4*s + 10 Hs = Ps/Qs # X(s) Señal de entrada xt = d # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [0, 0] # estado cero no se usan # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 10 muestras = 101 # 51 resolucion grafica