Ejemplos de solución a circuitos eléctricos que en el planteamiento se usan ecuaciones diferenciales ordinarias y se desarrollan usando la Transformada de Laplace. En el ejercicio 3 se desarrolla una malla que genera un sistema de ecuaciones EDO y se resuelve con transformadas de Laplace.
[Ej 1. RLC fuente DC e interruptor] [ Ej 2. RLC con Laplace ] [Ej 3. RC, RL, interruptor ]
Ejercicio 1. Circuito RLC, fuente DC e interruptor con transformada de Laplace
Referencia: Lathi Ej.4.13 p365
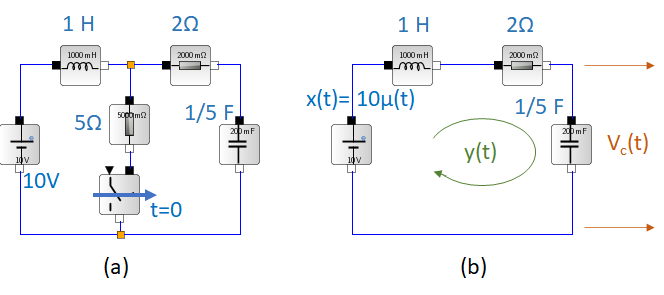
En el circuito de la figura, el interruptor se encuentra cerrado mucho tiempo antes de t=0. Cuando se abre en un instante, encuentre la corriente del inductor y(t) para t≥0.
El interruptor se encuentra cerrado por mucho tiempo, la corriente por el inductor es 2 A y el voltaje del capacitor es 10 V, pues el inductor en DC opera como un conductor sin resistencia y el capacitor se encuentra completamente cargado.
Cuando se abre el interruptor, el circuito se equivalente es el mostrado en la derecha, La corriente inicial del inductor es y(0-)=2 y el voltaje inicial del capacitor Vc(0-)=10.
El voltaje en la entrada es 10 V, empezando en t=0 y puede ser representado como 10 μ(t) para simplificar la representación de la fuente DC y expresar que antes de t=0 se aplica las condiciones iniciales dadas.mientras se den las condiciones iniciales en t=0 solo será necesario saber que la corriente en t≥0 para determinar la respuesta en t≥0 .
La ecuación del circuito en luego de abrir el interruptor es:
\frac{\delta}{\delta t}y(t) + 2 y8t) + 5 \int_{-\infty}^{t}y(\tau) \delta \tau = 10 \mu(t)Las condiciones iniciales se aplican como:
\frac{\delta}{\delta t}y(t) = sY(s) - y(0^-)= sY(s)-2 \int_{-\infty}^{t} y(\tau) \delta \tau = \frac{1}{s}Y(s) + \frac{1}{s} \int_{-\infty}^{0^-}y(\tau) \delta \tauy(t) es la corriente del capacitor, por lo que el integral es:
\int_{-\infty}^{0^-}y(\tau) \delta \tau = q_C(0^-) = CV_c (0^-) = \frac{1}{5}10 = 2por lo que la parte del capacitor es:
\int_{-\infty}^{t}y(\tau) \delta \tau = \frac{1}{s}Y(s) + \frac{2}{s}La transformada de Laplace de la ecuación integro diferencial del circuito RLC al usar los resultados se reescribe como:
sY(s)-2+2Y(s)+ 5\frac{1}{s}Y(s) + 5\frac{2}{s} = \frac{10}{s} sY(s)+2Y(s)+ 5\frac{1}{s}Y(s) = \frac{10}{s} +2 - 5\frac{2}{s} \Big[ s+2+\frac{5}{s}\Big]Y(s) =2 \Big[ s^2+2s+5\Big]Y(s) = 2 s Y(s) = \frac{2 s}{s^2+2s+5}El polinomio del denominador tiene raíces complejas
>>> import sympy as sym
>>> s = sym.Symbol('s')
>>> Qs = s**2+2*s+5
>>> sym.roots(Qs)
{-1 - 2*I: 1, -1 + 2*I: 1}
por lo que es conveniente usar la forma cuadrática de la transformada de Laplace, donde A= 1, B=0, a=1, c=5, siendo,
r=\sqrt{\frac{20}{4}} = \sqrt{5} b=\sqrt{c-a^2} = 2 \theta=\tan^{-1} \Big(\frac{2}{4} \Big) = 0.46364 rad = 26.56^{o}usando la tabla de transformadas,
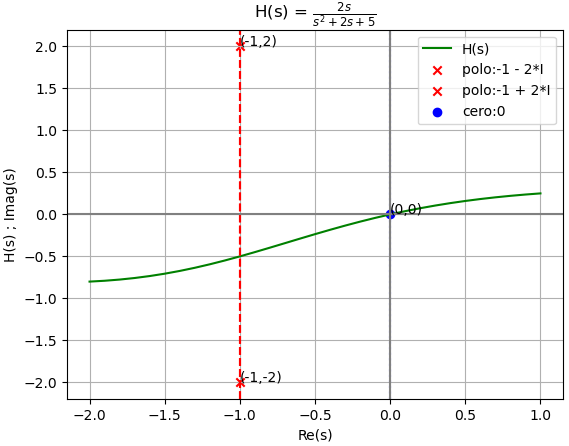
y(t) = \sqrt{5} e^{-t} cos (2t+0.46364) \mu (t)El gráfico de polos de la función de transferencia en el dominio s:
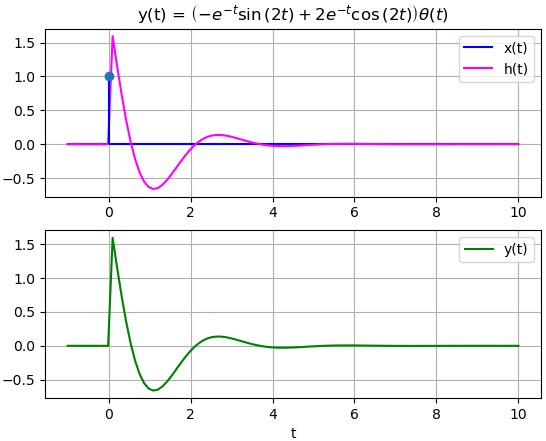
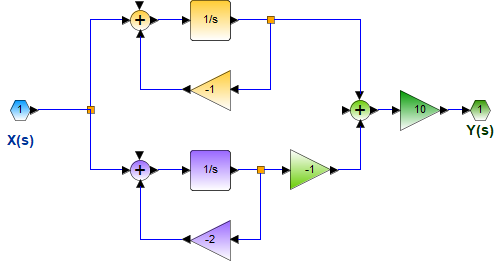
que generan una respuesta de salida y(t)
si la entrada x(t) es un impulso unitario, la respuesta es la misma que h(t)
La respuesta del algoritmo obtenida es:
H(s) = P(s)/Q(s):
2*s
------------
2
s + 2*s + 5
H(s) en factores:
2*s
------------
2
s + 2*s + 5
H(s) parámetros cuadraticos:
2*s/(s**2 + 2*s + 5) : {'A': 2.0, 'B': 0, 'a': 1.0,
'c': 5.0, 'r': 2.23606797749979, 'b': 2.0,
'theta': 0.4636476090008061}
h(t) :
/ -t -t \
\- e *sin(2*t) + 2*e *cos(2*t)/*Heaviside(t)
polosceros:
Q_polos : {-1 - 2*I: 1, -1 + 2*I: 1}
P_ceros : {0: 1}
Estabilidad de H(s):
n_polos_real : 0
n_polos_imag : 2
enRHP : 0
unicos : 0
repetidos : 0
asintota : estable
X(s):
1
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0
ZSR respuesta estado cero:
ZSR :
2*s
------------
2
s + 2*s + 5
ZSR_Qs2 :
2*s/(s**2 + 2*s + 5) :
{'A': 2.0, 'B': 0, 'a': 1.0, 'c': 5.0,
'r': 2.23606797749979, 'b': 2.0,
'theta': 0.4636476090008061}
yt_ZSR :
/ -t -t \
\- e *sin(2*t) + 2*e *cos(2*t)/*Heaviside(t)
Y(s)_total = ZIR + ZSR:
2*s
------------
2
s + 2*s + 5
y(t)_total = ZIR + ZSR:
/ -t -t \
\- e *sin(2*t) + 2*e *cos(2*t)/*Heaviside(t)
>>>
Instrucciones en Python
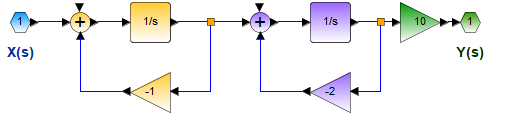
Usando los bloques desarrollados en la y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta.
# Y(s) Respuesta total con entada cero y estado cero # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # https://blog.espol.edu.ec/telg1001/ import sympy as sym import matplotlib.pyplot as plt import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) d = sym.DiracDelta(t) u = sym.Heaviside(t) # H(s) respuesta impulso Ps = 2*s Qs = s**2 + 2*s + 5 Hs = Ps/Qs # X(s) Señal de entrada xt = d # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [0, 0] # estado cero no se usan # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 10 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO Hs = fcnm.apart_s(Hs) # fracciones parciales Hs_fc = fcnm.factor_exp(Hs) # en factores Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc) polosceros = fcnm.busca_polosceros(Hs) Q_polos = polosceros['Q_polos'] P_ceros = polosceros['P_ceros'] estable = fcnm.estabilidad_asintotica_s(Q_polos) # H(t) respuesta al impulso ht = 0*s term_suma = sym.Add.make_args(Hs) for term_k in term_suma: ht_k = sym.inverse_laplace_transform(term_k,s,t) # simplifica log(exp()) ej: e**(-2s)/(s**2) if ht_k.has(sym.log): ht_k = sym.simplify(ht_k,inverse=True) ht = ht + ht_k lista_escalon = ht.atoms(sym.Heaviside) ht = sym.expand(ht,t) # terminos suma ht = sym.collect(ht,lista_escalon) # PROCEDIMIENTO Respuesta ZIR, ZSR Xs = fcnm.laplace_transform_suma(xt) # ZIR_s respuesta entrada cero de s sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio) ZIR = sol_ZIR['ZIR'] yt_ZIR = sol_ZIR['yt_ZIR'] # ZSR respuesta estado cero, Y(s) a entrada X(s) sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs) ZSR = sol_ZSR['ZSR'] yt_ZSR = sol_ZSR['yt_ZSR'] # Respuesta total Y(s) y y(t) Ys = ZIR + ZSR Ys = fcnm.apart_exp(Ys) yt = yt_ZIR + yt_ZSR lista_escalon = yt.atoms(sym.Heaviside) yt = sym.collect(yt,lista_escalon) # SALIDA print(' H(s) = P(s)/Q(s):') sym.pprint(Hs) print(' H(s) en factores:') sym.pprint(Hs_fc) if len(Hs_Qs2)>0: print('\nH(s) parámetros cuadraticos:') fcnm.print_resultado_dict(Hs_Qs2) print('\n h(t) :') sym.pprint(ht) print('\npolosceros:') fcnm.print_resultado_dict(polosceros) print('\nEstabilidad de H(s):') for k in estable: print('',k,':',estable[k]) print('\n X(s): ') sym.pprint(Xs) print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales') if not(sol_ZIR == sym.nan): # existe resultado fcnm.print_resultado_dict(sol_ZIR) else: print(' insuficientes condiciones iniciales') print(' revisar los valores de cond_inicio[]') print('\n ZSR respuesta estado cero:') fcnm.print_resultado_dict(sol_ZSR) print('\n Y(s)_total = ZIR + ZSR:') sym.pprint(Ys) print('\n y(t)_total = ZIR + ZSR:') sym.pprint(yt) # Graficas polos, H(s), con polos h(t) -------- figura_s = fcnm.graficar_Fs(Hs,Q_polos,P_ceros,f_nombre='H',solopolos=True) figura_Hs = fcnm.graficar_Fs(Hs,Q_polos,P_ceros,muestras,f_nombre='H') figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h') # GRAFICAS y(t),x(t),h(t) --------------------- figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras) plt.show()
[Ej 1. RLC fuente DC e interruptor] [ Ej 2. RLC con Laplace ] [Ej 3. RC, RL, interruptor ]
Ejemplo 2. Circuito RLC con transformada de Laplace
Referencia: Lathi Ejemplo 4.17 p375
Realice el análisis de la corriente i(t) en el circuito mostrado en la figura, suponiendo que todas las condicioes iniciales son cero.
El primer paso es representar el circuito en el dominio de la frecuencia (s), mostrado a la derecha de la figura. Se representan los voltajes y corrientes usando la transformada de Laplace.
El voltaje 10μ(t) se representa como 10/s y la corriente i(t) como I(s). Todos los elementos del circuito se muestran con su respectiva impedancia. El inductor de 1 henrio se representa por s, el capacitor de 1/3 faradio se representa por 2/s. El resistor de 3 ohms es solo 3.
El voltaje en el circuito V(s) en cualquier elemento es I(s) por su impedancia Z(s).
La impedancia del circuito para el lazo es:
Z(s) = s+3+\frac{2}{s} = \frac{s^2+3s+2}{s}el voltaje de entrada es V(s)=10/s, por lo que la fórmula básica de corriente es:
I(s) =\frac{V(s)}{Z(s)} = \frac{10/s}{(s^2+3s+2)/s} I(s) = \frac{10}{(s^2+3s+2)}usando las raíces del denominador,
I(s) =\frac{10}{(s+1)(s+2)}aplicando fracciones parciales:
I(s) = \frac{10}{s+1} -\frac{10}{s+2}Aplicando la transformada inversa,
i(t) = 10*(e^{-t}-e^{-2t}) \mu (t)[Ej 1. RLC fuente DC e interruptor] [ Ej 2. RLC con Laplace ] [Ej 3. RC, RL, interruptor ]
Ejemplo 3. Circuito RC y RL, fuente DC e interruptor con transformada de Laplace
Referencia: Lathi ejemplo 4.18 p378
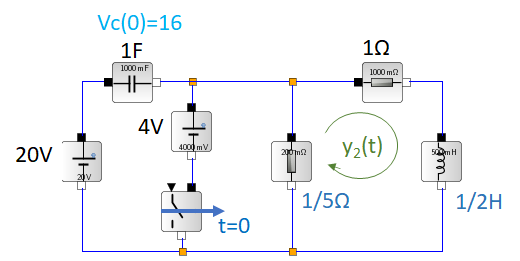
El interruptor está en posición cerrada por un largo tiempo antes de que sea abierto en t=0. Encuentre las corrientes y1(t) y y2(t) para t>0
Al revisar el circuito se observa que cuando el interruptor esta cerrado y se han alcanzado las condiciones de estado estable, el voltaje del capacitor Vc=16 V y la corriente del inductor y2= 4 .
Las fuentes de 20V y 4V se pueden también ordenar en forma equivalente
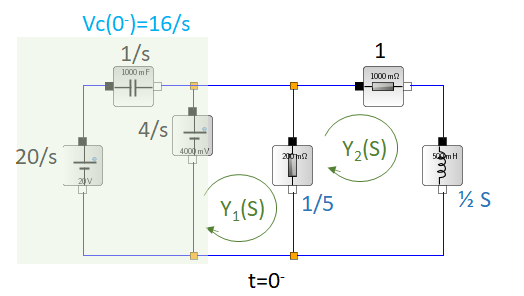
Cuando se abre el interruptor en t=0, las condiciones iniciales son Vc(0-)=16 y y2(0-)= 4 como se muestra en la versión con transformada de Laplace en la figura anterior. La ecuación diferencial del circuito para suma de voltajes en la malla en el lazo 1 y la tabla de propiedades de la transformada de Laplace para la integración aplicada al capacitor,
-\frac{20}{s} + \frac{1}{s}\Big[Y_1(s)+ \int_{-\infty}^{0^-} y_1(\tau) \delta \tau \Big] + \frac{1}{5} \Big[Y_1(s)-Y_2(s) \Big] = 0 -\frac{20}{s} + \frac{1}{s}\Big[Y_1(s) + 16 \Big] + \frac{1}{5} Y_1(s) - \frac{1}{5}Y_2(s) = 0 -\frac{20}{s} + \frac{1}{s}Y_1(s) +\frac{16}{s} + \frac{1}{5}Y_1(s)-\frac{1}{5}Y_2(s) = 0 \Big[ \frac{1}{s}+ \frac{1}{5}\Big] Y_1(s)-\frac{1}{5}Y_2(s) = \frac{4}{s} \frac{1}{5}\Big[ \frac{5+s}{s}\Big] Y_1(s)-\frac{1}{5}Y_2(s) = \frac{4}{s} \Big[ \frac{5+s}{s}\Big] Y_1(s)-Y_2(s) = \frac{20}{s}>>> import sympy as sym >>> s = sym.Symbol('s') >>> ecuacion1 = -20/s+(1/s)*(Y1+16)+(1/5)*Y1-(1/5)*Y2 >>> ecuacion1.expand() 0.2*Y1 + Y1/s - 0.2*Y2 - 4/s
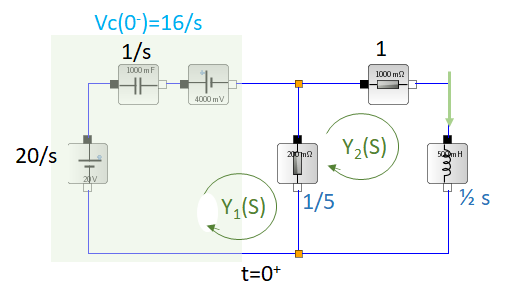
El voltaje inicial del capacitor se puede representar por un voltaje en serie 16/s y la corriente inicial del inductor de 4 A que representa una fuente de valor VL = Ly2(0-) = 1/2(4) = 2. La ecuación diferencial del lazo 2 y usando la transformada de Laplace para la derivada con condiciones iniciales para el inductor,
\frac{1}{5}\Big[Y_2(s)-Y_1(s)\Big] + 1 Y_2(s) + \frac{1}{2} \Big[ sY_2(s) - Y_2(0^-)\big] = 0 \Big[\frac{1}{5}+ 1\Big] Y_2(s) -\frac{1}{5}Y_1(s) + \frac{1}{2} \Big[ sY_2(s) - 4 \Big] = 0 \frac{6}{5} Y_2(s) -\frac{1}{5}Y_1(s) + \frac{1}{2} sY_2(s) - 4\frac{1}{2} = 0 -\frac{1}{5}Y_1(s) +\Big[ \frac{6}{5} + \frac{1}{2} s\Big] Y_2(s) = 2 -Y_1(s) +\Big[ \frac{12+5s}{2}\Big] Y_2(s) = 10el resultado obtenido com Sympy, como una instrucción adicional a la anterior,
>>> ecuacion2 = (1/5)*(Y2-Y1)+Y2+(1/2)*(s*Y2-4) >>> ecuacion2.expand() -0.2*Y1 + 0.5*Y2*s + 1.2*Y2 - 2.0
Con lo que hay que resolver el sistema de ecuaciones:
\begin{cases} \Big[ \frac{s+5}{s}\Big] Y_1(s)-Y_2(s) = \frac{20}{s} \\ -Y_1(s) +\Big[ \frac{12+5s}{2}\Big] Y_2(s) = 10 \end{cases}multipicando la primera ecuación por (s/(5+s)) y sumando con la segunda
\begin{cases} Y_1(s)-\frac{s}{s+5}Y_2(s) = \frac{20}{s}\frac{s}{s+5} \\ -Y_1(s) +\Big[ \frac{12+5s}{2}\Big] Y_2(s) = 10 \end{cases} -\frac{s}{s+5}Y_2(s) + \frac{12+5s}{2}Y_2(s) = \frac{20}{s+5} + 10 \Big[ -\frac{s}{s+5} + \frac{12+5s}{2} \Big] Y_2(s) = 10\Big[\frac{2+(s+5)}{s+5}\Big] \Big[ \frac{-2s+(s+5)(12+5s)}{2(s+5)}\Big] Y_2(s) = 10\frac{2+s+5}{s+5} (-2s+12s+5s^2 +60+25s) Y_2(s) = 20(s+7) (5s^2 +35s +60) Y_2(s) = 20(s+7) 5(s^2 +7s +12) Y_2(s) = 20(s+7) Y_2(s) = 4\frac{s+7}{s^2 +7s +12}las raices del denominador son s=-4 y s=-3
Y_2(s) = 4\frac{s+7}{(s+3)(s+4)}usando fracciones parciales y el método de Heaviside,
k_1 = 4\frac{s+7}{\cancel{(s+3)}(s+4)} \Big|_{s=-3} = 4\frac{(-3)+7}{(-3+4)} = 4\frac{4}{1} = 16 k_2 = 4\frac{s+7}{(s+3)\cancel{(s+4)}}\Big|_{s=-4} = 4\frac{(-4)+7}{(-4+3)}=4\frac{3}{-1} = - 12reescribiendo en fracciones parciales
Y_2(s) = \frac{16}{s+3} -\frac{12}{s+4}usando la tabla de transformadas de Laplace:
y_2(t) = (16 e^{-3t}-12e^{-4t}) \mu (t)de forma semejante se puede resolver para Y1(s) al reemplazar el resultado en la primera ecuación del sistema de ecuaciones,
\Big[ \frac{s+5}{s}\Big] Y_1(s)-Y_2(s) = \frac{20}{s} \Big[ \frac{s+5}{s}\Big] Y_1(s)-\Big[\frac{16}{s+3} -\frac{12}{s+4}\Big] = \frac{20}{s} Y_1(s) = \frac{s}{s+5} \Big[\frac{16}{s+3} -\frac{12}{s+4} + \frac{20}{s}\Big] Y_1(s) = \frac{s}{s+5}\frac{16}{s+3} - \frac{s}{s+5}\frac{12}{s+4} + \frac{s}{s+5}\frac{20}{s} Y_1(s) = 16\frac{s}{(s+5)(s+3)} - 12\frac{s}{(s+5)(s+4)} + \frac{20}{s+5}realizando las fracciones parciales con método de Heaviside para los dos primeros términos,
>>> import sympy as sym
>>> s = sym.Symbol('s')
>>> ya = 16*s/((s+5)*(s+3))
>>> ya.apart()
40/(s + 5) - 24/(s + 3)
>>> yb = -12*s/((s+5)*(s+4))
>>> yb.apart()
-60/(s + 5) + 48/(s + 4)
>>>
Y_1(s) = \frac{40}{s+5} -\frac{24}{s+3} - \frac{60}{s+5}+\frac{48}{s+4} + \frac{20}{s+5}
Y_1(s) = -\frac{24}{s+3} +\frac{48}{s+4}
aplicando desde la tabla la transformada inversa de Laplace,
y_1(t) = (-24e^{-3t} +48e^{-4t} ) \mu (t)Instrucciones con Python
la solución del sistema de ecuaciones con transformadas de Laplace se puede realizar con Sympy
Y1 (s):
24*s + 48
-------------
2
s + 7*s + 12
Y1 (s) en fracciones parciales:
48 24
----- - -----
s + 4 s + 3
Y2 (s):
4*s + 28
-------------
2
s + 7*s + 12
Y2 (s) en fracciones parciales:
12 16
- ----- + -----
s + 4 s + 3
>>>
# Sistemas de ecuaciones con Sympy import sympy as sym # INGRESO s = sym.Symbol('s') [Y1, Y2] = sym.symbols('Y1 Y2') ecuacion1 = ((s+5)/s)*Y1 - Y2 -20/s ecuacion2 = -Y1 + +((12+5*s)/2)*Y2 -10 variables = [Y1,Y2] # PROCEDIMIENTO respuesta = sym.solve([ecuacion1, ecuacion2], variables) # SALIDA for cadarespuesta in respuesta: print(str(cadarespuesta) +'(s):') sym.pprint(respuesta[cadarespuesta]) print('') print(str(cadarespuesta)+'(s) en fracciones parciales:') sym.pprint(respuesta[cadarespuesta].apart())
[Ej 1. RLC fuente DC e interruptor] [ Ej 2. RLC con Laplace ] [Ej 3. RC, RL, interruptor ]