Referencia: Lathi Ejemplo 4.12 p361
Resuelva la ecuación diferencial de segundo orden usando respuesta a entrada cero y respuesta a estado cero.
(D^2 + 5D + 6) y(t) = (D+1) x(t)para las condiciones iniciales y(0-)=2 y y'(0-)=1, ante la entrada
x(t) = e^{-4t} \mu (t)El ejercicio muestra nuevamente el concepto sobre la respuesta total del sistema tiene dos componentes:
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
Respuesta del sistema a: [ entrada cero ZIR ] [ estado cero ZSR ] [total ]
..
1. Respuesta a entrada cero y condiciones iniciales
Si el sistema bajo observación se no tiene señal de entrada X(s) = 0, la parte de estado cero no aporta componente de salida.
| Respuesta total |
= | respuesta a entrada cero ZIR |
+ | respuesta a estado cero ZSR |
Sin embargo, si existen valores iniciales en los componentes del sistema (circuito con capacitores), se producirá una respuesta a entrada cero que básicamente responde a las condiciones iniciales al sistema.
Referencia: Lathi Ejemplo 4.12 p361
Un sistema LTI tiene la ecuación diferencial de segundo orden expresada con operadores D:
(D^2 + 5D + 6) y(t) = (D+1) x(t)El sistema tiene las condiciones iniciales y(0-)=2 y y'(0-)=1.
1.1 Desarrollo Analítico para Respuesta a entrada cero y condiciones iniciales
La ecuación se escribe usando la transformada de Laplace:
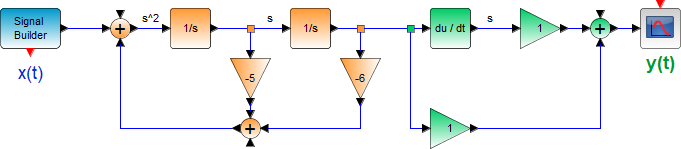
(s^2 + 5s + 6) Y(s) = (s+1) X(s)El diagrama básico de la expresión LTI, sin simplificar, se muestra en la figura. La sección de color naranja representa Q(s) y la sección en verde representa P(s)
Para el análisis de entrada cero X(s)=0, la ecuación se simplifica a
(s^2 + 5s + 6) Y(s) = 0Las condiciones iniciales se aplican usando la tabla de propiedades de Laplace, donde se muestra que los valores iniciales se añaden a los componentes de primera y segunda derivada:
\frac{\delta}{\delta t} y(t) \Longleftrightarrow sY(s) - y(0^{-}) = sY(s) -2 \frac{\delta^2}{\delta t^2} y(t) \Longleftrightarrow s^2 Y(s) - sy(0^{-}) - y'(0^{-}) = s^2 Y(s) -2s - 1Se recuerda que para la entrada x(t) = 0, no se crean términos en el lado derecho de la expresión
[s^2 Y(s) -2s - 1] + 5[sY(s) -2] + 6Y(s) = 0Agrupando los terminos Y(s), se tienen los componentes que no dependen de Y(s) que son los resultantes de las condiciones iniciales.
[s^2 + 5s + 6]Y(s) - (2s+11) = 0 [s^2 + 5s + 6]Y(s) = (2s+11) Y(s)= \frac{2s+11}{s^2 + 5s + 6}El resultado Y(s) corresponde al término de entrada cero con condiciones iniciales aplicadas.
Aplicando un algoritmo en Python para añadir los componentes de condiciones iniciales, el resultado es:
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero :
2*s + 11
ZIR :
5 7
- ----- + -----
s + 3 s + 2
yt_ZIR :
/ -2*t -3*t\
\7*e - 5*e /*Heaviside(t)
>>>
1.2 Desarrollo con Sympy-Python
Se inicia con los resultados de algoritmos anteriores, donde se ingresan las expresiones de Q(s) y P(s) correspondientes a H(s). Las condiciones iniciales se ingresan en un arreglo en orden de derivada descendente, por ejemplo para el ejercicio [y'(0), y(0)] = [1., 2.]
Par generar las expresiones de condición inicial, se genera el término de condición cero o term_cero, compuesto de los términos de orden tomados del vector inicial.
# Y_ZIR(s) Respuesta entrada cero con Transformada de Laplace # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # Ejemplo Lathi 4.12 p361 # https://blog.espol.edu.ec/telg1001/ import sympy as sym import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) # H(s) respuesta impulso Ps = s + 1 Qs = s**2 + 5*s + 6 Hs = Ps/Qs #Hs = 6*sym.exp(-2*s)/s**2 # X(s) Señal de entrada Xs = 0*s # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [1, 2] # PROCEDIMIENTO def respuesta_ZIR_s(Hs,cond_inicio): '''respuesta a entrada cero ZIR con H(s) y condiciones de inicio Si ZIR es sym.nan existen insuficientes condiciones ''' polosceros = fcnm.busca_polosceros(Hs) Q_polos = polosceros['Q_polos'] # coeficientes y grado de Q Q = 1+0*s for raiz in Q_polos: veces = Q_polos[raiz] Q = Q*((s-raiz)**veces) Q = sym.poly(Q,s) Q_coef = Q.all_coeffs() # coeficientes Q Q_grado = Q.degree() # grado polinomio Q term_cero = 0*s if len(cond_inicio) == Q_grado: for j in range(0,Q_grado,1): term_orden = 0 for i in range(j,Q_grado,1): term_orden = term_orden + cond_inicio[i]*(s**(i-j)) term_cero = term_cero + term_orden*Q_coef[j] ZIR = term_cero/Q ZIR = fcnm.apart_s(ZIR) ZIR_Qs2 = fcnm.Q_cuad_s_parametros(ZIR) else: ZIR = sym.nan # insuficientes condiciones iniciales if not(ZIR==sym.nan): # entrada_cero en t yt_ZIR = sym.inverse_laplace_transform(ZIR,s,t) # simplifica log(exp()) ej: e**(-2t)/(s**2) if yt_ZIR.has(sym.log): yt_ZIR = sym.simplify(yt_ZIR,inverse=True) lista_escalon = yt_ZIR.atoms(sym.Heaviside) yt_ZIR = sym.expand(yt_ZIR,t) # terminos suma yt_ZIR = sym.collect(yt_ZIR,lista_escalon) sol_ZIR ={'term_cero' : term_cero} if len(ZIR_Qs2)>0: # añade si Q es cuadratico sol_ZIR['ZIR_Qs2'] = ZIR_Qs2 sol_ZIR = sol_ZIR | {'ZIR' : ZIR, 'yt_ZIR': yt_ZIR} else: sol_ZIR = sym.nan return(sol_ZIR) # respuesta a entrada_cero ZIR en s sol_ZIR = respuesta_ZIR_s(Hs,cond_inicio) # SALIDA - polinomio print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales') if not(sol_ZIR == sym.nan): # existe resultado for k in sol_ZIR: print('\n',k,':') sym.pprint(sol_ZIR[k]) else: print(' insuficientes condiciones iniciales') print(' revisar los valores de cond_inicio[]')
El siguiente caso sería realizar el mismo sistema LTI CT, con respuesta Y(s) ante una extrada X(s), conocido también como estado cero.
Para mantenerlo simple, se consideraría condiciones iniciales en cero.
Finalmente se sumarían la entrada cero y estado cero para obtener la respuesta total.
Respuesta del sistema a: [ entrada cero ZIR ] [ estado cero ZSR ] [total ]
2. Respuesta a estado cero con x(t) de Sistema con ecuación diferencial de 2do orden
El ejercicio continua el desarrollo del concepto sobre la respuesta total del sistema tiene dos componentes:
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
| ZSR = h(t) ⊗ x(t) ZSR(s) = H(S) X(s) |
Referencia: Lathi Ejemplo 4.12 p361
Un sistema LTI tiene la ecuación diferencial de segundo orden expresada con operadores D:
(D^2 + 5D + 6) y(t) = (D+1) x(t)(viene de la sección anterior...) si se somete a la entrada,
x(t) = e^{-4t} \mu (t)2.1. Desarrollo Analítico para estado cero
Ahora, todos los componentes tienen condición inicial cero y una señal de entrada x(t). El diagrama de bloques del sistema se obtuvo en la sección anterior de "entrada cero":
En este caso se considera que ningún componente del sistema tiene valor inicial [0., 0.], interpretado por ejemplo como que todos los capacitores estan descargados, la salida corresponde solo a la parte conformada por x(t) y la respuesta al impulso h(t).
para la entrada x(t),
x(t) = e^{-4t} \mu(t) \Longleftrightarrow X(s) = \frac{1}{s+4}Usando transformadas de Laplace, la ecuación del sistema se convierte en:
[s^2 Y(s)] + 5[sY(s)] + 6Y(s) = (s+1)X(s)que al aplicar la parte de X(s),
[s^2 Y(s)] + 5[sY(s)] + 6Y(s) = (s+1)\frac{1}{s+4} (s^2 + 5s + 6) Y(s) = \frac{s+1}{s+4} Y(s) = \frac{s+1}{(s+4)(s^2 + 5s + 6)}que es equivalente a y(t) = h(t)⊗x(t) como convolución en dominio de tiempo o Y(s)=H(s)X(s) en el dominio de s.
Para simplificar la respuesta de la inversa de transformada de Laplace, se separa en fracciones parciales. Al usar el algoritmo en Python se obtiene:
Y(s) = -\frac{1}{2}\frac{1}{s+2} +2\frac{1}{s+3} - \frac{3}{2} \frac{1}{s+4}Tomando la referencia de la tabla de transformadas de Laplace, fila 5, se tiene:
y(t) = -\frac{1}{2} e^{-2t} \mu(t) + 2 e^{-3t} \mu(t) -\frac{3}{2} e^{-4t} \mu (t)2.2. Instrucciones con Sympy-Python
Para este caso se añade la transformada de Laplace X(s) de x(t). La expresión μ(t) se representa como Heaviside en Sympy.
Las instrucciones son semejantes a las usadas en algoritmos anteriores, tal como Hs = Ps/Qs, considerando que respuesta a estado cero es ZSR = Hs*Xs
Se refleja el resultado obtenido en el desarrollo analítico,
ZSR respuesta estado cero:
ZSR :
3 2 1
- --------- + ----- - ---------
2*(s + 4) s + 3 2*(s + 2)
yt_ZSR :
/ -2*t -4*t\
| e -3*t 3*e |
|- ----- + 2*e - -------|*Heaviside(t)
\ 2 2 /
>>>
las instrucciones usadas son:
# Y_ZSR(s) Respuesta estado cero con Transformada Laplace # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # Ejemplo Lathi 4.12 p361 # https://blog.espol.edu.ec/telg1001/ import sympy as sym import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) # H(s) respuesta impulso Ps = s + 1 Qs = s**2 + 5*s + 6 Hs = Ps/Qs # X(s) Señal de entrada Xs = 1/(s+4) # PROCEDIMIENTO def respuesta_ZSR_s(Hs,Xs): '''respuesta a estado cero ZSR con H(s) y X(s) ''' ZSR = Hs*Xs ZSR = fcnm.apart_s(ZSR) ZSR_Qs2 = fcnm.Q_cuad_s_parametros(ZSR) # ZSR respuesta estado cero(t) yt_ZSR = sym.inverse_laplace_transform(ZSR,s,t) # simplifica log(exp()) ej: e**(-2t)/(s**2) if yt_ZSR.has(sym.log): yt_ZSR = sym.simplify(yt_ZSR,inverse=True) lista_escalon = yt_ZSR.atoms(sym.Heaviside) yt_ZSR = sym.expand(yt_ZSR,t) # terminos suma yt_ZSR = sym.collect(yt_ZSR,lista_escalon) sol_ZSR = {'ZSR' : ZSR} if len(ZSR_Qs2)>0: sol_ZSR['ZSR_Qs2'] = ZSR_Qs2 sol_ZSR = sol_ZSR | {'yt_ZSR' : yt_ZSR} return(sol_ZSR) sol_ZSR = respuesta_ZSR_s(Hs,Xs) # SALIDA - polinomio print('\n ZSR respuesta estado cero:') for k in sol_ZSR: print('\n',k,':') sym.pprint(sol_ZSR[k])
El siguiente bloque consiste en hacer el ejercicio completo del sistema LTIC, considerando condiciones iniciales y una entrada x(t), que da la respuesta total del sistema.
Respuesta del sistema a: [ entrada cero ZIR ] [ estado cero ZSR ] [total ]
3. Y(s) respuesta total con condiciones iniciales y entrada x(t)
Finalmente se obtiene el resultado sumando los dos componentes desarrollados en los numerales anteriores
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
3.1 Desarrollo Analítico
Se incluye para mostrar que la respuesta total Y(s) = entrada_cero+estado_cero
Para resolver con transformadas de Laplace, la ecuación se expresa como :
\frac{\delta ^2}{\delta t^2} y(t) + 5 \frac{\delta}{\delta t} y(t) + 6 y(t) = \frac{\delta}{\delta t}x(t) +x(t)haciendo y(t) ⇔Y(s) y usando la tabla de propiedades
\frac{\delta}{\delta t} y(t) \Longleftrightarrow sY(s) - y(0^{-}) = sY(s) -2 \frac{\delta^2}{\delta t^2} y(t) \Longleftrightarrow s^2 Y(s) - sy(0^{-}) - y'(0^{-}) = s^2 Y(s) -2s - 1para la entrada x(t),
x(t) = e^{-4t} \mu(t) \Longleftrightarrow X(s) = \frac{1}{s+4} \frac{\delta}{\delta t}x(t) \Longleftrightarrow sX(s) - x(0^{-}) = s\frac{1}{s+4} -0 = \frac{s}{s+4}con lo que la ecuación diferencial en transformada de Laplace se escribe,
[s^2 Y(s) -2s - 1] + 5[sY(s) -2] + 6Y(s) = \frac{s}{s+4}+\frac{1}{s+4}Agrupando los terminos Y(s) y los términos de la derecha,
[s^2 + 5s + 6]Y(s) - (2s+11) = \frac{s+1}{s+4} [s^2 + 5s + 6]Y(s) = (2s+11) + \frac{s+1}{s+4} Y(s) = \frac{2s+11}{s^2 + 5s + 6} + \frac{s+1}{(s+4)(s^2 + 5s + 6)}despejando Y(s) se puede observar que la expresión es la suma de,
Y(s) = \text{entrada cero} + \text{estado cero} Y(s) = \frac{(s+4)(2s+11)+s+1}{(s+4)(s^2 + 5s + 6)} Y(s)= \frac{2s^2+20s+45}{(s^2 + 5s + 6)(s+4)} Y(s)= \frac{2s^2+20s+45}{(s+2)(s+3)(s+4)}expandiendo en fracciones parciales:
Y(s)= \Big(\frac{13}{2}\Big)\frac{1}{s+2} - 3\frac{1}{s+3} - \Big(\frac{3}{2}\Big)\frac{1}{s+4}Finalmente, usando la transformada inversa de Laplace obtener la expresión en el dominio de t,
Y(t)= \Big[ \frac{13}{2}e^{-2t} - 3 e^{-3t} - \frac{3}{2}e^{-4t} \Big] \mu(t)El ejercicio muestra la facilidad de resolver el sistema usando transformadas de Laplace.
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero :
2*s + 11
ZIR :
5 7
- ----- + -----
s + 3 s + 2
yt_ZIR :
/ -2*t -3*t\
\7*e - 5*e /*Heaviside(t)
ZSR respuesta estado cero:
ZSR :
3 2 1
- --------- + ----- - ---------
2*(s + 4) s + 3 2*(s + 2)
yt_ZSR :
/ -2*t -4*t\
| e -3*t 3*e |
|- ----- + 2*e - -------|*Heaviside(t)
\ 2 2 /
Y0(s) total = ZIR + ZSR:
3 3 13
- --------- - ----- + ---------
2*(s + 4) s + 3 2*(s + 2)
y(t) total = ZIR + ZSR:
/ -2*t -4*t\
|13*e -3*t 3*e |
|-------- - 3*e - -------|*Heaviside(t)
\ 2 2 /
>>>
3.2 Instrucciones Sympy-Python
Las instrucciones para respuesta a entrada cero ZIR y respuesta estado cero ZSR se integran en un algoritmo.
# Y(s) Respuesta total con entrada cero y estado cero # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # Ejemplo Lathi 4.12 p361 # https://blog.espol.edu.ec/telg1001/ import sympy as sym import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) # H(s) respuesta impulso Ps = s + 1 Qs = s**2 + 5*s + 6 Hs = Ps/Qs #Hs = 6*sym.exp(-2*s)/s**2 # X(s) Señal de entrada Xs = 1/(s+4) # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [1, 2] # PROCEDIMIENTO # ZIR_s respuesta entrada cero de s sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio) ZIR = sol_ZIR['ZIR'] yt_ZIR = sol_ZIR['yt_ZIR'] # ZSR respuesta estado cero, Y(s) a entrada X(s) sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs) ZSR = sol_ZSR['ZSR'] yt_ZSR = sol_ZSR['yt_ZSR'] # Respuesta total Y(s) y y(t) Ys = ZIR + ZSR Ys = fcnm.apart_s(Ys) yt = yt_ZIR + yt_ZSR lista_escalon = yt.atoms(sym.Heaviside) yt = sym.collect(yt,lista_escalon) # SALIDA - polinomio print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales') if not(sol_ZIR == sym.nan): # existe resultado for k in sol_ZIR: print('\n',k,':') sym.pprint(sol_ZIR[k]) else: print(' insuficientes condiciones iniciales') print(' revisar los valores de cond_inicio[]') print('\n ZSR respuesta estado cero:') for k in sol_ZSR: print('\n',k,':') sym.pprint(sol_ZSR[k]) print('\n Y0(s) total = ZIR + ZSR:') sym.pprint(Ys) print('\n y(t) total = ZIR + ZSR:') sym.pprint(yt)
Respuesta del sistema a: [ entrada cero ZIR ] [ estado cero ZSR ] [total ]