Se continúa con el ejercicio propuesto en la sección Sistema LTIC-Modelo entrada-salida:
Referencia: Lathi ejemplo 2.6 p166
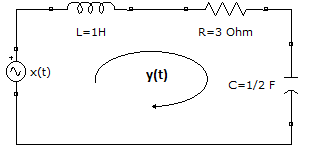En la entrada de sistema se aplica:
el sistema tiene respuesta a impulso:
h(t) = \big( 2e^{-2t} -e^{-t}\big)\mu (t)El ejemplo es continuación del presentado para respuesta a entrada cero, que tiene la ecuación:
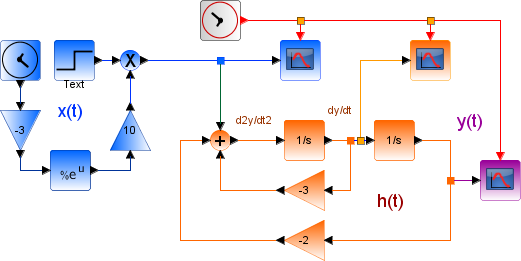
(D^2 + 3D +2)y(t) = Dx(t)Al diagrama desarrollado en la sección Respuesta entrada cero – Diagrama Bloques, se añaden los bloques para formar la señal de entrada x(t). La variable tiempo se indica con el Bloque Reloj, el escalón μ(t) se configura para empezar en cero y el valor -3 del exponente se los indica con un bloque de ganancia antes de eu.
Para diferenciación de los bloques por sección, la entrada se usa el color azul, el sistema en color naranja y la salida en color morado.
Para continuar con la simulación, asegúrese que no existan condiciones iniciales en el sistema, es decir los valores de estado inicial para los bloques 1/s se encuentren en cero.
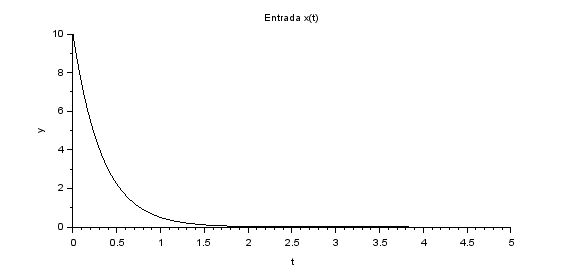
Los osciloscopios de observación, tienen su propia referencia de tiempo con otro reloj. El osciloscopio de la señal de entrada x(t) se muestra primero, y la salida en la gráfica posterior.
La señal de salida se obtiene de forma semejante a la respuesta a impulso, es decir en el punto donde está la primera derivada. Revisar teoría para aplicar la forma: P(D)[y(t)μ(t)], que en éste ejercicio se aplica una D.
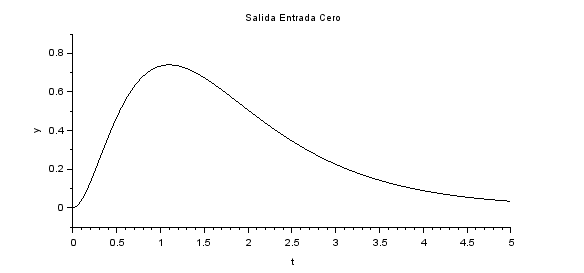
El resultado de y(t), solo como referencia, es el que se obtiene en el osciloscopio ubicado a la derecha abajo del diagrama.
Con lo que se muestra que es posible observar resultados usando algunos bloques en un simulador.