Referencia: Lathi Ejemplo 3.21 p286
Determine la respuesta a estado cero de un sistema LTID descrito por la ecuación de diferencias mostrada,
y[n+2] - 0.6 y[n+1] - 0.16 y[n] = 5x[n+2]Si la entrada es x[n] = 4-n u[n]
Para realizar el diagrama, se desplaza la ecuación en dos unidades
y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n] y[n] = 0.6 y[n-1] + 0.16 y[n-2] + 5x[n]las condiciones iniciales es estado cero son todas cero.
La entrada puede expresada como:
x[n] = 4^{-n} \mu [n] = \Big( \frac{1}{4} \Big)^n \mu [n] x[n] = 0.25^{n} \mu [n]la respuesta al impulso del sistema se encontró en el ejemplo de la sección anterior:
h[n] = [ (-0.2)^n +4 (0.8)^n ] \mu [n]Por lo que:
y[n] = x[n] \circledast h[n] = 0.25^{n} \mu [n] \circledast \Big[ (-0.2)^n +4 (0.8)^n \Big] \mu [n] = 0.25^{n} \mu [n] \circledast (-0.2)^n \mu [n] + 0.25^{n} \mu [n] \circledast 4 (0.8)^n \mu [n]usando la tabla de convolución de sumas para tener:
y[n] = \Bigg[ \frac{0.25^{n+1}-(-0.2)^{n+1}}{0.25-(-0.2)} + 4 \frac{0.25^{n+1} - 0.8^{n+1}}{0.25-0.8}\Bigg] \mu [n] = \Bigg[2.22 \Big[ 0.25^{n+1} - (-0.2)^{n+1}\Big] + - 7.27 \Big[ 0.25^{n+1} - (0.8)^{n+1}\Big]\Bigg] \mu [n] = \Big[ -5.05 (0.25)^{n+1} - 2.22(-0.2)^{n+1} + 7.27 (0.8)^{n+1} \Big] \mu [n]recordando que ϒn+1 = ϒ(ϒ)n se puede expresar,
y[n] = \Big[-1.26 (0.25)^{n} + 0.444 (-0.2)^{n} +5.81(0.8)^{n}\Big] \mu [n]Desarrollo numérico con Python
La respuesta a estado cero se encuentra en forma numérica con la expresión:
y[n] = x[n] \circledast h[n]que en Numpy es np.convolve() y facilita el cálculo de la convolucion de sumas. El tema de convolución con Python se desarrolla en la siguiente sección.
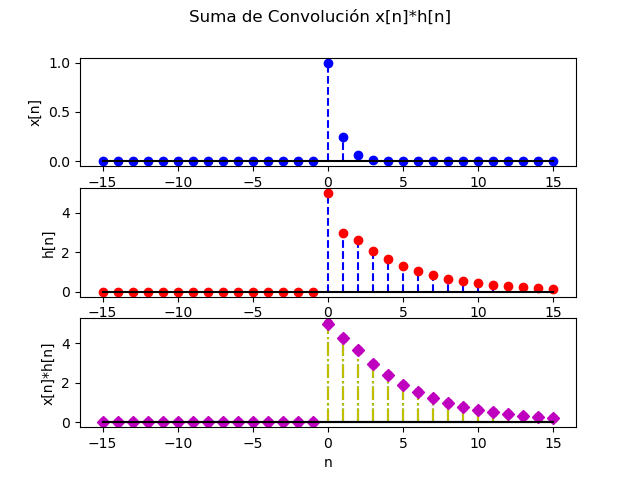
La respuesta del algoritmo se presenta en la gráfica:
En el algoritmo se compara la solución numérica yi[n] con la solución analítica yia[n], obteniendo un error del orden 10-3 dado por el truncamiento de dígitos en ambos métodos.
error numerico vs analítico: maximo de |error|: 0.006000000000000227 errado: [-0. 0. -0. 0. -0. 0. -0. 0. -0. 0. -0. -0. -0. 0. 0. -0.006 -0.0058 -0.00509 -0.0041445 -0.00334173 -0.00267831 -0.0021442 -0.00171569 -0.00137264 -0.00109813 -0.00087851 -0.00070281 -0.00056225 -0.0004498 -0.00035984 -0.00028787]
El algoritmo continúa como un anexo a los algoritmos de respuesta a entrada cero e impulso.
Instrucciones en Python
# Sistema LTID. Respuesta entrada cero, # Respuesta a impulso # resultado con raices Reales # ejercicio lathi ejemplo 3.121 p286 import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO # coeficientes E con grado descendente Q = [1., -0.6, -0.16] P = [5., 0, 0 ] # condiciones iniciales con n ascendente -2,-1, 0 inicial = [25/4, 0.] # PROCEDIMIENTO # raices gamma = np.roots(Q) # revisa raices numeros complejos revisaImag = np.iscomplex(gamma) escomplejo = np.sum(revisaImag) if escomplejo == 0: # coeficientes de ecuacion m = len(Q)-1 A = np.zeros(shape=(m,m),dtype=float) for i in range(0,m,1): for j in range(0,m,1): A[i,j] = gamma[j]**(-m+i) ci = np.linalg.solve(A,inicial) # ecuacion yn n = sym.Symbol('n') y0 = 0 for i in range(0,m,1): y0 = y0 + ci[i]*(gamma[i]**n) # Respuesta impulso ni = np.arange(-m,m,1) hi = np.zeros(m, dtype=float) xi = np.zeros(2*m, dtype=float) xi[m] = 1 # impulso en n=0 # h[n] iterativo p_n = len(P) for i in range(0,m,1): for k in range(m,2*m,1): hi[i] = hi[i] - Q[k-m]*hi[m-k+1] for k in range(0,p_n,1): hi[i] = hi[i] + P[k]*xi[m+i] Bh = hi[:m] # coeficientes de ecuacion m = len(Q)-1 Ah = np.zeros(shape=(m,m),dtype=float) for i in range(0,m,1): for j in range(0,m,1): Ah[i,j] = gamma[j]**(i) ch = np.linalg.solve(Ah,Bh) # ecuacion hn hn = 0 for i in range(0,m,1): hn = hn + ch[i]*(gamma[i]**n) # Respuesta de estado cero ---------------- # Rango [a,b], simetrico a 0 b = 15 ; a = -b u = lambda n: np.piecewise(n,[n>=0,n<0],[1,0]) x = lambda n: (0.25)**(n)*u(n) hL = sym.lambdify(n,hn,'numpy') h = lambda n: hL(n)*u(n) # PROCEDIMIENTO ni = np.arange(a,b+1,1) xi = x(ni) hi = h(ni) # Suma de Convolucion x[n]*h[n] yi = np.convolve(xi,hi,'same') # compara respuesta numerica con resultado analitico ya = lambda n: (-1.26*(0.25**n)+0.444*((-0.2)**n)+5.81*(0.8**n))*u(n) yia = ya(ni) errado = yia-yi erradomax = np.max(np.abs(errado)) # SALIDA print('respuesta entrada cero: ') print('raices: ', gamma) if escomplejo == 0: print('Matriz: ') print(A) print('Ci: ', ci) print('yn: ') sym.pprint(y0) print('\n respuesta impulso: ') print('hi:',hi) print('Matriz: ') print(Ah) print('Ch: ',ch) print('n>=0, hn: ') sym.pprint(hn) print('\n error numerico vs analitico: ') print(' maximo de abs(error): ', erradomax) print(' errado: ') print(errado) # SALIDA - GRAFICA plt.figure(1) plt.suptitle('Suma de Convolucion x[n]*h[n]') plt.subplot(311) plt.stem(ni,xi, linefmt='b--', markerfmt='bo',basefmt='k-') plt.ylabel('x[n]') plt.subplot(312) plt.stem(ni,hi, linefmt='b--', markerfmt='ro',basefmt='k-') plt.ylabel('h[n]') plt.subplot(313) plt.stem(ni,yi, linefmt='g-.', markerfmt='mo', basefmt='k-') plt.stem(ni,yia, linefmt='y-.', markerfmt='mD', basefmt='k-') plt.ylabel('x[n]*h[n]') plt.xlabel('n') plt.show() else: print(' existen raices con números complejos.') print(' usar algoritmo de la sección correspondiente.')