6.1.2 Sistema LTI DT – Solución iterativa

Ejercicio 1

Referencia: Lathi ejemplo 3.11 p266

Un sistema LTID tiene la siguiente expresión:

y[n] - 0.5 y[n-1] = x[n]

con condiciones iniciales y[-1]=16 y entrada causal x[n] = n² μ[n] ,para n>=0.

Desarrollo analítico

La expresión se reordena,

y[n] = 0.5 y[n-1] + x[n]

Para n=0, y la condición y[-1]=16

y[0] = 0.5 y[0-1] + x[0] = 0.5 y[-1] + 0^2 = 0.5(16) + 0 = 8

Para n=1,

y[1] = 0.5 y[1-1] + x[1] = 0.5 y[0] + 1^2 = 0.5(8) + 1 = 5

Para n=2,

y[2] = 0.5 y[2-1] + x[2] = 0.5 y[1] +2^2 = 6.5

Para n=3,

y[3] = 0.5 y[3-1] + x[3] = 0.5 y[2] + 3^2 = 0.5 (6.5) + 9 = 12.25

y así sucesivamente.

El algoritmo en Python presenta el resultado en forma gráfica y en forma de valores.

los resultados numéricos son:

muestras:  10
[[  n,  xi,  yi]]
[[ -1.     0.    16.  ]
 [  0.     0.     8.  ]
 [  1.     1.     5.  ]
 [  2.     4.     6.5 ]
 [  3.     9.    12.25]
 [  4.    16.    22.12]
 [  5.    25.    36.06]
 [  6.    36.    54.03]
 [  7.    49.    76.02]
 [  8.    64.   102.01]
 [  9.    81.   132.  ]]
>>>

El diagrama realizado para la ecuación tiene dos partes, el generador de señal en azul y la parte del sistema en color gris para el retrazo y naranja para el coeficiente de retrazo:

---

Ejercicio 2

Referencia: Lathi ejemplo 3.12 p267

Resolver de forma iterativa,

y[n+2] - y[n+1] +0.24y[n] = x[n+2] - 2x[n+1]

con las condiciones iniciales de y[-1] = 2, y[-2] =1 y entrada causal x[n]=n que inicia en n=0

Desarrollo

Se deja como tarea realizar la solución analítica con lapiz y papel, se continua con el uso del algoritmo para la solución.

Si la ecuación se reescribe de la forma:

y[n+2] = y[n+1] - 0.24y[n] + x[n+2] - 2x[n+1]

y se desplaza en el tiempo con retrasos, para adaptarla al algoritmo presentado en el ejemplo anterior.

y[n] = y[n-1] - 0.24y[n-2] + x[n] - 2x[n-1]

Las condiciones iniciales ordenadas son inicial= [1,2]

se emplea el mismo algoritmo, adaptando la fórmula par x[n] y y[n],teniendo los resultados siguientes:

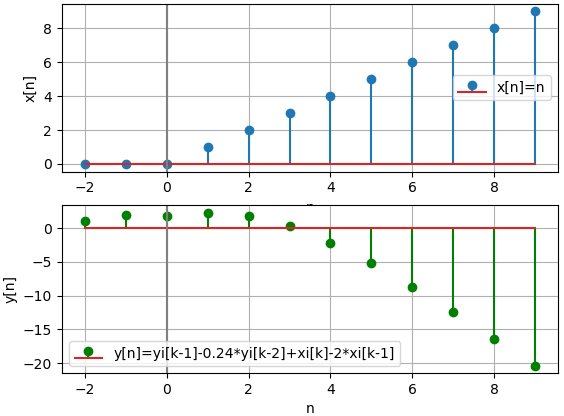
muestras:  10
[[  n,  xi,  yi]]
[[ -2.     0.     1.  ]
 [ -1.     0.     2.  ]
 [  0.     0.     1.76]
 [  1.     1.     2.28]
 [  2.     2.     1.86]
 [  3.     3.     0.31]
 [  4.     4.    -2.14]
 [  5.     5.    -5.21]
 [  6.     6.    -8.7 ]
 [  7.     7.   -12.45]
 [  8.     8.   -16.36]
 [  9.     9.   -20.37]]
>>>

la gráfica correspondiente es: