Edison Del Rosario – Página 14 – Señales y Sistemas

9 agosto, 20174 febrero, 2023

1Eva2009TII_T2 LTI DT bloques, respuesta impulso y paso

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 2. (20 puntos) Un estudiante del curso de Sistemas Lineales ha encontrado que un determinado sistema LTI-DT causal, en el dominio del tiempo tiene la siguiente representación:

Determinar:

a. La respuesta impulso h[n]

b. La respuesta de paso s[n]

c. ¿Es el sistema BIBO estable?, justifique su respuesta.

9 agosto, 20174 febrero, 2023

1Eva2009TII_T1 LTI CT diagrama canónico y respuesta a impulso

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 1. (20 puntos) Un estudiante del curso de Sistemas Lineales ha encontrado que un determinado sistema puede ser realizable mediante el diagrama canónico mostrado en la siguiente figura.

Determinar,

a. La función de transferencia del mencionado sistema

b. su respuesta impulso h(t)

c. ¿Qué puede decir acerca de la estabilidad interna y externa?

Referencia: Ejemplo 3, LTIC Laplace – Diagramas de bloques con «1/s»

9 agosto, 20174 febrero, 2023

1Eva2009TII_T5 LTI DT bloques H[z] en serie

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 5. (20 puntos) El sistema que se muestra en la siguiente figura, es el resultante de la combinación de dos subsistemas conectados en cascada.

Determinar:

1. Las respuestas impulso de cada subsistema y del sistema completo, es decir h₁[n], h₂[n], h[n].

h₁[n]
h₂[n]
h[n]

2. Su respuesta y[n]=s]n], expresada a la mínima expresión frente a la siguiente excitación x[n]=μ[n], esquematícela.

9 agosto, 20174 febrero, 2023

1Eva2009TII_T4 LTI CT con entrada x(t) tipo coseno

1ra Evaluación II Término 2009-2010. 3/Diciembre/2009. TELG1001

Tema 4. (20 puntos) El diagrama de polos y ceros de un sistema de segundo orden cuya función de transferencia H(s) es mostrado en la siguiente figura, donde se conoce que la respuesta DC de este sistema es -1. es decir H(j0)=-1.

a. Conociendo el hecho que:

H(s) = \frac{k (s^2 + b_1 s + b_2)}{s^2 + a_1 s + a_2}

determinar el valor de las constantes k, b₁,b₂, a₁ y a₂.

b. Encontrar la respuesta y(t) que este sistema tendría, frente a la siguiente entrada:

x(t) = 4+\cos \Big(\frac{1}{2}t +\frac{\pi}{3}\Big)

c. Comente justificadamente acerca de la estabilidad interna y externa del mencionado sistema.

9 agosto, 20174 febrero, 2023

s1Eva2009TII_T5 LTI DT bloques H[z] en serie

Referencia: 1Eva2009TII_T5 LTI DT bloques H[z] en serie

1. Las respuestas impulso de cada subsistema

H_1[z] = \frac{z}{z-(0.7)} = \frac{z}{z-0.7}

usando la tabla de transformadas z

h_1[n] = (0.7)^n \mu[n]

Continuando con el subsistema de la derecha

H_2[z] = \frac{z}{z-(-0.5)} = \frac{z}{z+0.5}

h_2[n] = (-0.5)^n \mu[n]

El sistema total:

H[z] = H_1[z] H_2[z] = \frac{z}{(z-0.7)} \frac{z}{(z+0.5)} = \frac{z^2}{(z-0.7)(z+0.5)}

fracciones parciales modificadas, multiplica ambos lados por 1/z

\frac{H[z]}{z} = \Big( \frac{1}{z} \Big) \frac{z^2}{(z-0.7)(z+0.5)}= \frac{z}{(z-0.7)(z+0.5)}

\frac{H[z]}{z} = \frac{z}{(z-0.7)(z+0.5)} = \frac{k_1}{z-0.7} +\frac{k_2}{z+0.5}

k_1 = \frac{z}{\cancel{(z-0.7)}(z+0.5)} \Big|_{z=0.7} = \frac{0.7}{(0.7+0.5)} = 0.5833

k_2 = \frac{z}{(z-0.7)\cancel{(z+0.5)}} \Big|_{z=-0.5} = \frac{-0.5}{(-0.5-0.7)} = 0.4166

\frac{H[z]}{z} = \frac{0.5833}{z-0.7} +\frac{0.4166}{z+0.5}

Restaura fracciones parciales, multiplica ambos lados por z

H[z] = \frac{0.5833 z}{z-0.7} +\frac{0.4166z}{z+0.5}

usando la tabla de transformadas z

h[n] = 0.5833 \Big(0.7 \Big)^n \mu[n] +0.4166 \Big(-0.5\Big)^n \mu[n]

factor común μ[n]

h[n] = \Bigg( 0.5833 \Big(0.7 \Big)^n +0.4166 \Big(-0.5\Big)^n \Bigg) \mu[n]

Revisando el resultado con el algoritmo en Python

 Hz:
          2        
         z         
-------------------
(z - 0.7)*(z + 0.5)

 Hz/z:
          z          
---------------------
     2               
1.0*z  - 0.2*z - 0.35

 Hz/z.apart:
0.416666666666667   0.583333333333333
----------------- + -----------------
   1.0*z + 0.5         1.0*z - 0.7   

 Hz = (Hz/z)*z
0.416666666666667*z   0.583333333333333*z
------------------- + -------------------
    1.0*z + 0.5           1.0*z - 0.7    
 
polos:     {-0.500000000000000: 1, 0.700000000000000: 1}

 polos Re:  [-1/2, 7/10]

Tarea: 2. Su respuesta y[n]=s]n], expresada a la mínima expresión frente a la siguiente excitación x[n]=μ[n], esquematícela.

Instrucciones en Python

Algoritmos desarrollados en X[z] Fracciones parciales modificadas con Python

y la parte gráfica de Transformada z con Sympy-Python

# Transformada z- Fracciones parciales
# Polos únicos, repetidos y complejos
# Lathi Ejercicio 5.3c pd495
# blog.espol.edu.ec/telg1001
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
z = sym.Symbol('z')

Pz = z**2
Qz = (z-0.7)*(z+0.5)

# PROCEDIMIENTO
P = Pz.as_poly(z)
Q = Qz.as_poly(z)
Xz = Pz/Qz

# Raices Denominador
Q_raiz = sym.roots(Q)
Q_raizRe = sym.real_roots(Q)
rcompleja = len(Q_raiz)-len(Q_raizRe)

# Raices reales, únicas y repetidas
if (rcompleja<=0 and len(Q_raizRe)>0):
    # fracciones parciales modificadas
    Xzz = (P/Q)/z
    Xzm = Xzz.apart()
    # fracciones parciales restaurada
    terminos = Xzm.args
    Xzp = 0*z
    for untermino in terminos:
        Xzp = Xzp + untermino*z

def parametro_cuadratico(untermino):
    unparametro ={}
    # revisa denominador cuadratico
    [numerador,denominador] = (untermino).as_numer_denom()
    gradoD = 0
    coeficientesD = denominador
    gradoN = 0
    coeficientesN = numerador
    if not(denominador.is_constant()):
        denominador = denominador.as_poly()
        gradoD = denominador.degree()
        coeficientesD = denominador.coeffs()
    if not(numerador.is_constant()):
        numerador = numerador.as_poly()
        gradoN = numerador.degree()
        coeficientesN = numerador.coeffs()
    if gradoD == 2 and gradoN==2:
        a = float(coeficientesD[1])/2
        gamma2 = float(coeficientesD[2])
        gamma = np.sqrt(gamma2)
        A = float(coeficientesN[0])
        B = float(coeficientesN[1])
        rN = (A**2)*gamma2 + B**2 - 2*A*a*B
        rD = gamma2 - a**2
        r = np.sqrt(rN/rD)
        beta = np.arccos(-a/gamma)
        thetaN = A*a-B
        thetaD = A*np.sqrt(gamma2-a**2)
        theta = np.arctan(thetaN/thetaD)
        unparametro = {'r':r,
                       'gamma':gamma,
                       'beta':beta,
                       'theta':theta}
    return (unparametro)

# Terminos cuadraticos
parametros = [] # denominador cuadratico
if (rcompleja>0 and len(Q_raizRe)>0):
    # fracciones parciales modificadas
    Xzz = (P/Q)/z
    Xzm = Xzz.apart()
    # fracciones parciales restaurada
    terminos = Xzm.args
    Xzp = 0*z
    for untermino in terminos:
        Xzp = Xzp + untermino*z
        unparam = parametro_cuadratico(untermino*z)
        if len(unparam)>0:
            parametros.append(unparam)
if (rcompleja>0 and len(Q_raizRe)==0):
    Xzp = P/Q
    parametros.append(parametro_cuadratico(P/Q))

# SALIDA
print('\n Hz:')
sym.pprint(Xz)
if (len(Q_raizRe)>0):
    print('\n Hz/z:')
    sym.pprint(Xzz)
    print('\n Hz/z.apart:')
    sym.pprint(Xzm)
    print('\n Hz = (Hz/z)*z')
    sym.pprint(Xzp)
    print('\n polos:    ', Q_raiz)
print('\n polos Re: ', Q_raizRe)
if len(parametros)>0:
    for unparam in parametros:
        print('parametros cuadraticos: ')
        for cadauno in unparam.keys():
            print(cadauno,'\t',unparam[cadauno])


# grafica plano z imaginario
figura, grafROC = plt.subplots()
# limite
radio1 = plt.Circle((0,0),1,color='lightgreen',
                    fill=True)
radio2 = plt.Circle((0,0),1,linestyle='dashed',
                    color='lightgreen',fill=False)
grafROC.add_patch(radio1)
for raiz in Q_raiz.keys():
    [r_real,r_imag] = raiz.as_real_imag()
    radio_raiz = np.abs(raiz)
    nROC = plt.Circle((0,0),radio_raiz,
                      color='red',fill=True)
    grafROC.add_patch(nROC)
grafROC.add_patch(radio2) # borde r=1
grafROC.axis('equal')
# marcas de r=1 y valor a
for raiz in Q_raiz.keys():
    [r_real,r_imag] = raiz.as_real_imag()
    grafROC.plot(r_real,r_imag,'o',color='orange',
             label ='polo:'+str(float(raiz))+';'+str(Q_raiz[raiz]))
grafROC.plot(1,0,'o',color='green',
         label ='radio:'+str(1))

plt.axhline(0,color='grey')
plt.axvline(0,color='grey')
plt.grid()
plt.legend()
plt.xlabel('Re[z]')
plt.ylabel('Imag[z]')
untitulo = 'ROC H[z]='+str(Xz)
plt.title(untitulo)

# h[n] usando tabla de transformadas
m = 10
n = sym.Symbol('n')
hn = 0.5833*((0.7)**n)*sym.Heaviside(n)+0.4166*((-0.5)**n)*sym.Heaviside(n)
fn = sym.lambdify(n,hn)
ki = np.arange(0,m,1)
xnk = fn(ki)

# grafica h[n]
figura, grafxn = plt.subplots()
plt.stem(ki,xnk)
plt.xlabel('ki')
plt.ylabel('h[n]')
plt.title('h[n]= '+str(hn))
plt.show()

9 agosto, 201720 marzo, 2023

s1Eva2009TII_T3 LTI CT y(t) desde h(t) y x(t) con términos escalón desplazados

Ejercicio: 1Eva2009TII_T3 LTI CT y(t) desde h(t) y x(t) con términos escalón desplazados

La función de transferencia h(t) y la señal de entrada x(t) son,

x(t) = 2 μ(t-1) – 2 μ(t-3)

h(t) = μ(t+1) – 2 μ(t-1) + μ(t-3)

La primera observación es que h(t) h(t) tiene un componente No causal, que se adelanta en tiempo μ(t+1) a x(t). La transformada unilateral de Laplace no aplica para este término, por lo que para el algoritmo se usa la entrada X(s) y se evita el error en la transformada. Por lo demás el algoritmo funciona bien.
Tarea: Revisar y justificar

Usando la función de transferencia h(t) con las transformadas de Laplace H(s)

H(s) = \frac{1}{s}e^{s} - 2\frac{1}{s}e^{-s}+ \frac{1}{s} e^{-3s}

simplificando la expresión como F(s)*(terminos exponenciales)

H(s) = \frac{1}{s} \Big[ e^{s} - 2e^{-s}+ e^{-3s} \Big]

tiene la forma gráfica,

La señal de entrada usando las transformadas de Laplace X(s)

X(s) = 2\frac{1}{s}e^{-s} - 2\frac{1}{s}e^{-3s}

X(s) = \frac{2}{s} \Big[e^{-s} - e^{-3s} \Big]

La señal de salida Y(s)=H(s)*X(s)

Y(s) = \frac{2}{s^2} \Big[ e^{s} - 2e^{-s}+ e^{-3s} \Big] \Big[e^{-s} - e^{-3s} \Big]

multiplicando los términos de exponenciales

Y(s) = \frac{2}{s^2} \Big[ e^{s}e^{-s} - 2e^{-s}e^{-s}+ e^{-3s}e^{-s} - e^{s}e^{-3s} + 2e^{-s}e^{-3s} - e^{-3s}e^{-3s} \Big]

Y(s) = \frac{2}{s^2} \Big[ 1 - 2e^{-2s}+ e^{-4s}- e^{-2s} + 2e^{-4s} - e^{-6s} \Big]

Y(s) = \frac{2}{s^2} \Big[ 1 - 3e^{-2s}+ 3e^{-4s} - e^{-6s} \Big]

usando la tabla de transformadas de Laplace en forma inversa:

y(t) = 2 (t) \mu (t) -6 (t-2) \mu (t-2) +6(t-4) \mu (t-4) -2(t-6) \mu(t-6) \Big]

La respuesta al impulso H(s)no tiene polos en el lado derecho del plano s, por lo que las salidas son acotadas, en consecuencia el sistema es asintoticamente estable y también BiBO estable.

usando el algoritmo, considerando que las condiciones iniciales son cero,:

 H(s) = P(s)/Q(s):
 s      -s    -3*s
e    2*e     e    
-- - ----- + -----
s      s       s  
 H(s) en factores:
 s      -s    -3*s
e    2*e     e    
-- - ----- + -----
s      s       s  

 h(t) :
Heaviside(t - 3) - 2*Heaviside(t - 1) + Heaviside(t + 1)

polosceros:
exp(s) : {'Q_polos': {0: 1}, 'P_ceros': {}, 'Hs_k': 1/s}
exp(-3*s) : {'Q_polos': {0: 1}, 'P_ceros': {}, 'Hs_k': 1/s}
exp(-s) : {'Q_polos': {0: 1}, 'P_ceros': {}, 'Hs_k': -2/s}
Q_polos : {0: 1}
P_ceros : {}

Estabilidad de H(s):
 n_polos_real : 0
 n_polos_imag : 1
 enRHP : 0
 unicos : 0
 repetidos : 0
 asintota : estable

 X(s): 
   -s      -3*s
2*e     2*e    
----- - -------
  s        s   

Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0

 ZSR respuesta estado cero:
ZSR :
        -2*s      -4*s      -6*s
2    6*e       6*e       2*e    
-- - ------- + ------- - -------
 2       2         2         2  
s       s         s         s   
yt_ZSR :
2*t*Heaviside(t) + (12 - 6*t)*Heaviside(t - 2) + (12 - 2*t)*Heaviside(t - 6) +
 (6*t - 24)*Heaviside(t - 4)

 Y(s)_total = ZIR + ZSR:
        -2*s      -4*s      -6*s
2    6*e       6*e       2*e    
-- - ------- + ------- - -------
 2       2         2         2  
s       s         s         s   

 y(t)_total = ZIR + ZSR:
2*t*Heaviside(t) + (12 - 6*t)*Heaviside(t - 2) + (12 - 2*t)*Heaviside(t - 6) +
 (6*t - 24)*Heaviside(t - 4)
>>>

Usando los bloques desarrollados en la Unidad 4 Sistemas LTI – Laplace y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta.

# Y(s) Respuesta total con entada cero y estado cero
# Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs
# http://blog.espol.edu.ec/telg1001/
import sympy as sym
import matplotlib.pyplot as plt
import telg1001 as fcnm

# INGRESO
s = sym.Symbol('s')
t = sym.Symbol('t', real=True)
d = sym.DiracDelta(t)
u = sym.Heaviside(t)

# H(s) respuesta impulso
Hs = sym.exp(s)/s - 2*sym.exp(-s)/s + sym.exp(-3*s)/s

# X(s) Señal de entrada
xt = 2*u.subs(t,t-1) - 2*u.subs(t,t-3)

# condiciones iniciales, [y'(0),y(0)] orden descendente
t0 = 0
cond_inicio = [0] # estado cero no se usan

# Grafica, intervalo tiempo [t_a,t_b]
t_a = -2 ; t_b = 8
muestras = 101  # 51 resolucion grafica

# PROCEDIMIENTO
Hs = fcnm.apart_s(Hs) # fracciones parciales
Hs_fc = fcnm.factor_exp(Hs) # en factores
Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc)

polosceros = fcnm.busca_polosceros(Hs)
Q_polos = polosceros['Q_polos']
P_ceros = polosceros['P_ceros']

estable = fcnm.estabilidad_asintotica_s(Q_polos)

# H(t) respuesta al impulso
ht = 0*s
term_suma = sym.Add.make_args(Hs)
for term_k in term_suma:
    ht_k = sym.inverse_laplace_transform(term_k,s,t)
    # simplifica log(exp()) ej: e**(-2s)/(s**2)
    if ht_k.has(sym.log):
        ht_k = sym.simplify(ht_k,inverse=True)
    ht  = ht + ht_k
lista_escalon = ht.atoms(sym.Heaviside)
ht = sym.expand(ht,t) # terminos suma
ht = sym.collect(ht,lista_escalon)

# PROCEDIMIENTO Respuesta ZIR, ZSR
Xs = fcnm.laplace_transform_suma(xt)

# ZIR_s respuesta entrada cero de s
sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio)
ZIR = sol_ZIR['ZIR']
yt_ZIR = sol_ZIR['yt_ZIR']

# ZSR respuesta estado cero, Y(s) a entrada X(s)
sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs)
ZSR = sol_ZSR['ZSR']
yt_ZSR = sol_ZSR['yt_ZSR']

# Respuesta total Y(s) y y(t)
Ys = ZIR + ZSR
Ys = fcnm.apart_s(Ys)
yt = yt_ZIR + yt_ZSR
lista_escalon = yt.atoms(sym.Heaviside)
yt = sym.collect(yt,lista_escalon)

# SALIDA
print(' H(s) = P(s)/Q(s):')
sym.pprint(Hs)
print(' H(s) en factores:')
sym.pprint(Hs_fc)
if len(Hs_Qs2)>0:
    print('\nH(s) parámetros cuadraticos:')
    fcnm.print_resultado_dict(Hs_Qs2)

print('\n h(t) :')
sym.pprint(ht)

print('\npolosceros:')
fcnm.print_resultado_dict(polosceros)

print('\nEstabilidad de H(s):')
for k in estable:
    print('',k,':',estable[k])

print('\n X(s): ')
sym.pprint(Xs)
print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales')

if not(sol_ZIR == sym.nan): # existe resultado
    fcnm.print_resultado_dict(sol_ZIR)
else:
    print(' insuficientes condiciones iniciales')
    print(' revisar los valores de cond_inicio[]')

print('\n ZSR respuesta estado cero:')
fcnm.print_resultado_dict(sol_ZSR)

print('\n Y(s)_total = ZIR + ZSR:')
sym.pprint(Ys)
print('\n y(t)_total = ZIR + ZSR:')
sym.pprint(yt)

# Graficas polos, H(s), con polos h(t) --------
muestras_H = 101
figura_s  = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,f_nombre='H',solopolos=True)
figura_Hs = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,muestras=muestras_H,f_nombre='H')
figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h')
# GRAFICAS y(t),x(t),h(t) ---------------------
figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras)
plt.show()

9 agosto, 20174 febrero, 2023

s1Eva2009TII_T2 LTI DT bloques, respuesta impulso y paso

Ejercicio: 1Eva2009TII_T2 LTI DT bloques, respuesta impulso y paso

literal a. Respuesta al impulso, o H(s) del diagrama de bloques

a.1 H[z] Función de transferencia

Referencia: LTI DT – H[z] Diagrama de bloques con «1/z»

Dado que hay dos bloques (1/z) o de retraso , se identifica que los polinomios son de segundo orden (N=2). Los coeficientes de retraso se leen de arriba hacia abajo como a₀,-a₁,-a₂ ordenados en la siguiente tabla:

coeficientes
retraso	adelanto
a₀ = 1	b₀ = 1
a₁ = -(3/4) = -3/4	b₁ = 0
a₂ = -(-1/8) = 1/8	b₂ = 0

Se aplica lo mismo para los coeficientes de adelanto y se completa el modelo para los polinomios del numerador y denominador:

H[z] = \frac{b_0 z^N +b_1 z^{N-1} + \text{ ... } + b_{N-1} z + b_N}{z^N + a_1 z^{N-1} +\text{ ... } + a_{N-1}z +a_N}

H[z] = \frac{z^2}{z^2 - \frac{3}{4} z+\frac{1}{8}}

a.2 H[z] en fracciones parciales

fracciones parciales modificadas,

\frac{H[z]}{z} = \Big( \frac{1}{z} \Big) \frac{z^2}{z^2 - \frac{3}{4} z+\frac{1}{8}} = \frac{z}{z^2 - \frac{3}{4} z+\frac{1}{8}}

El polinomio del denominador es:

Q[z] = z^2 - \frac{3}{4} z+\frac{1}{8}

con raíces en 1/4 y 1/2

con lo que se obtiene la expresión para usar el método de «cubrir» de Heaviside

\frac{H[z]}{z} = \frac{z}{(z-1/4)(z-1/2)}= \frac{k_1}{z-1/4}+ \frac{k_2}{z-1/2}

k_1 = \frac{z}{\cancel{(z-1/4)}(z-1/2)}\Big|_{z=1/4} = \frac{1/4}{(1/4-1/2)} = -1

k_2 = \frac{z}{(z-1/4)\cancel{(z-1/2)}}\Big|_{z=1/2} = \frac{1/2}{(1/2-1/4)} = 2

\frac{H[z]}{z} = \frac{-1}{z-1/4}+ \frac{2}{z-1/2}

fracciones parciales

H[z] = \frac{-z}{z-1/4}+ \frac{2z}{z-1/2}

Revisando el resultado con el algoritmo en Python:

 Hz:
          2        
         z         
-------------------
 2                 
z  - 0.75*z + 0.125

 Hz/z:
           z           
-----------------------
     2                 
1.0*z  - 0.75*z + 0.125

 Hz/z.apart:
       1             2.0    
- ------------ + -----------
  1.0*z - 0.25   1.0*z - 0.5

 Hz = (Hz/z)*z
       z            2.0*z   
- ------------ + -----------
  1.0*z - 0.25   1.0*z - 0.5

 polos:     {0.250000000000000: 1, 0.500000000000000: 1}

 polos Re:  [1/4, 1/2]

Se obtiene h[n] usando la tabla de transformadas z

 Hz = (Hz/z)*z
       z            2.0*z   
- ------------ + -----------
  1.0*z - 0.25   1.0*z - 0.5

h[n] = - \Big(\frac{1}{4}\Big)^n \mu[n]+2\Big( \frac{1}{2} \Big)^n \mu[n]

a.3. Estabilidad del sistema

Los polos son menores que un radio de 1.
La ROC para el primer polo |z|>1/4 y para el segundo polo es |z|>1/2

Observaciones:

Las raíces características o frecuencias naturales del sistema se encuentran dentro del círculo de radio unitario. El sistema es asintóticamente estable, que implica que es BIBO estable.

h[n] no es de la forma k δ[n], por lo que el sistema global es con memoria.

a.4 Instrucciones con Python

Usando los algoritmo de la sección LTID Transformada z – X[z] Fracciones parciales modificadas con Python se adapta para el ejercicio

# Transformada z- Fracciones parciales
# Polos únicos, repetidos y complejos
# Lathi Ejercicio 5.3c pd495
# blog.espol.edu.ec/telg1001
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
z = sym.Symbol('z')

Pz = z**2
Qz = z**2-(3/4)*z+1/8

# PROCEDIMIENTO
P = Pz.as_poly(z)
Q = Qz.as_poly(z)
Xz = Pz/Qz

# Raices Denominador
Q_raiz = sym.roots(Q)
Q_raizRe = sym.real_roots(Q)
rcompleja = len(Q_raiz)-len(Q_raizRe)

# Raices reales, únicas y repetidas
if (rcompleja<=0 and len(Q_raizRe)>0):
    # fracciones parciales modificadas
    Xzz = (P/Q)/z
    Xzm = Xzz.apart()
    # fracciones parciales restaurada
    terminos = Xzm.args
    Xzp = 0*z
    for untermino in terminos:
        Xzp = Xzp + untermino*z

def parametro_cuadratico(untermino):
    unparametro ={}
    # revisa denominador cuadratico
    [numerador,denominador] = (untermino).as_numer_denom()
    gradoD = 0
    coeficientesD = denominador
    gradoN = 0
    coeficientesN = numerador
    if not(denominador.is_constant()):
        denominador = denominador.as_poly()
        gradoD = denominador.degree()
        coeficientesD = denominador.coeffs()
    if not(numerador.is_constant()):
        numerador = numerador.as_poly()
        gradoN = numerador.degree()
        coeficientesN = numerador.coeffs()
    if gradoD == 2 and gradoN==2:
        a = float(coeficientesD[1])/2
        gamma2 = float(coeficientesD[2])
        gamma = np.sqrt(gamma2)
        A = float(coeficientesN[0])
        B = float(coeficientesN[1])
        rN = (A**2)*gamma2 + B**2 - 2*A*a*B
        rD = gamma2 - a**2
        r = np.sqrt(rN/rD)
        beta = np.arccos(-a/gamma)
        thetaN = A*a-B
        thetaD = A*np.sqrt(gamma2-a**2)
        theta = np.arctan(thetaN/thetaD)
        unparametro = {'r':r,
                       'gamma':gamma,
                       'beta':beta,
                       'theta':theta}
    return (unparametro)

# Terminos cuadraticos
parametros = [] # denominador cuadratico
if (rcompleja>0 and len(Q_raizRe)>0):
    # fracciones parciales modificadas
    Xzz = (P/Q)/z
    Xzm = Xzz.apart()
    # fracciones parciales restaurada
    terminos = Xzm.args
    Xzp = 0*z
    for untermino in terminos:
        Xzp = Xzp + untermino*z
        unparam = parametro_cuadratico(untermino*z)
        if len(unparam)>0:
            parametros.append(unparam)
if (rcompleja>0 and len(Q_raizRe)==0):
    Xzp = P/Q
    parametros.append(parametro_cuadratico(P/Q))

# SALIDA
print('\n Hz:')
sym.pprint(Xz)
if (len(Q_raizRe)>0):
    print('\n Hz/z:')
    sym.pprint(Xzz)
    print('\n Hz/z.apart:')
    sym.pprint(Xzm)
    print('\n Hz = (Hz/z)*z')
    sym.pprint(Xzp)
    print('\n polos:    ', Q_raiz)
print('\n polos Re: ', Q_raizRe)
if len(parametros)>0:
    for unparam in parametros:
        print('parametros cuadraticos: ')
        for cadauno in unparam.keys():
            print(cadauno,'\t',unparam[cadauno])


# grafica plano z imaginario
figura, grafROC = plt.subplots()
# limite
radio1 = plt.Circle((0,0),1,color='lightgreen',
                    fill=True)
radio2 = plt.Circle((0,0),1,linestyle='dashed',
                    color='lightgreen',fill=False)
grafROC.add_patch(radio1)
for raiz in Q_raiz.keys():
    [r_real,r_imag] = raiz.as_real_imag()
    radio_raiz = np.abs(raiz)
    nROC = plt.Circle((0,0),radio_raiz,
                      color='red',fill=True)
    grafROC.add_patch(nROC)
grafROC.add_patch(radio2) # borde r=1
grafROC.axis('equal')
# marcas de r=1 y valor a
for raiz in Q_raiz.keys():
    [r_real,r_imag] = raiz.as_real_imag()
    grafROC.plot(r_real,r_imag,'o',color='orange',
             label ='polo:'+str(float(raiz))+';'+str(Q_raiz[raiz]))
grafROC.plot(1,0,'o',color='green',
         label ='radio:'+str(1))

plt.axhline(0,color='grey')
plt.axvline(0,color='grey')
plt.grid()
plt.legend()
plt.xlabel('Re[z]')
plt.ylabel('Imag[z]')
untitulo = 'ROC H[z]='+str(Xz)
plt.title(untitulo)

# h[n] usando tabla de transformadas
m = 10
n = sym.Symbol('n')
hn = 0.5833*((0.7)**n)*sym.Heaviside(n)+0.4166*((-0.5)**n)*sym.Heaviside(n)
fn = sym.lambdify(n,hn)
ki = np.arange(0,m,1)
xnk = fn(ki)

# grafica h[n]
figura, grafxn = plt.subplots()
plt.stem(ki,xnk)
plt.xlabel('ki')
plt.ylabel('h[n]')
plt.title('h[n]= '+str(hn))
plt.show()

literal b. La respuesta de paso s[n]

La señal de entrada será x[n] = μ[n], con transformada z de:

X[z] = \frac{z}{z-1}

b.1 Y[z] ante entrada X[z] y con función de transferencia H[z]

Usando el resultado de la respuesta al impulso,

H[z] = \frac{-z}{z-1/4}+ \frac{2z}{z-1/2}

La salida Y[n] del sistema será:

Y[z] = X[z] H[z] = \frac{z}{z-1} \Bigg[ \frac{-z}{z-1/4} + \frac{2z}{z-1/2} \Bigg]

b.2 Y[z] en fracciones parciales

Fracciones parciales modificadas

\frac{Y[z]}{z} = \frac{1}{z-1} \Bigg[ \frac{-z}{z-1/4} + \frac{2z}{z-1/2} \Bigg]

\frac{Y[z]}{z} = \frac{1}{(z-1)} \frac{-z}{z-1/4} + \frac{1}{(z-1)}\frac{2z}{z-1/2}

La expresión se puede operar por partes:

\frac{-z}{(z-1)(z-1/4)} = \frac{k_1}{z-1} + \frac{k_2}{z-1/4}

k_1 = \frac{-z}{\cancel{(z-1)}(z-1/4)} \Big|_{z=1} = \frac{-1}{(1-1/4)}=-\frac{4}{3}

k_2 = \frac{-z}{(z-1)\cancel{(z-1/4)}} \Big|_{z=1/4} = \frac{-1/4}{(1/4-1)} = \frac{1}{3}

y la segunda parte,

\frac{2z}{(z-1)(z-1/2)} = \frac{k_3}{z-1} + \frac{k_4}{z-1/2}

k_3 = \frac{2z}{\cancel{(z-1)}(z-1/2)} \Big|_{z=1} = \frac{2(1)}{1-1/2} = 4

k_4 = \frac{2z}{(z-1)\cancel{(z-1/2)}} \Big|_{z=1/2} = \frac{2(1/2)}{1/2-1} = -2

Uniendo las partes de fracciones parciales modificadas se tiene:

\frac{Y[z]}{z} = \frac{-4/3}{z-1} + \frac{1/3}{z-1/4} + \frac{4}{z-1}+\frac{-2}{z-1/2}

restaurando las fraciones parciales

Y[z] = \frac{8}{3}\frac{z}{z-1} + \frac{1}{3}\frac{z}{z-1/4} -2\frac{z}{z-1/2}

Usando la tabla de transformadas z

y[n] = \frac{8}{3}\mu [n] + \frac{1}{3}\Big( \frac{1}{4}\Big)^n \mu [n] -2 \Big(\frac{1}{2}\Big) ^n \mu[n]

Usando el algoritmo en Python, se tiene:

 Yz:
              3             
             z              
----------------------------
(z - 1)*(z - 0.5)*(z - 0.25)

 Yz/z:
                 2                
                z                 
----------------------------------
     3         2                  
1.0*z  - 1.75*z  + 0.875*z - 0.125

 Yz/z.apart:
0.333333333333333       2.0       2.66666666666667
----------------- - ----------- + ----------------
   1.0*z - 0.25     1.0*z - 0.5        z - 1      

 Yz = (Yz/z)*z
0.333333333333333*z      2.0*z      2.66666666666667*z
------------------- - ----------- + ------------------
    1.0*z - 0.25      1.0*z - 0.5         z - 1       

 polos:  {0.2500: 1, 0.5000: 1, 1.0000: 1}

gráfica de salida y[n]

9 agosto, 201720 marzo, 2023

s1Eva2009TII_T1 LTI CT diagrama canónico y respuesta a impulso

Ejercicio: 1Eva2009TII_T1 LTI CT diagrama canónico y respuesta a impulso

a. A partir del diagrama canónico se puede reordenar, identificando las partes del numerador P(s) y denominador Q(s) para escribir la función de transferencia;

reordenando diagrama:

escribiendo la ecuación como:

H(s) = \Big[ \frac{1}{s^2+3s+2}\Big]\Big[ 3s+2\Big] e^{-3s}

H(s) = \Big[ \frac{3s+2}{s^2+3s+2}\Big] e^{-3s}

Se usan los polos de la expresión para el denominador Q, para realizar las fracciones parciales:

 {polos,veces}:  {-1: 1, -2: 1}

H(s) = \Big[ \frac{3s+2}{(s+2)(s+1)} \Big] e^{-3s}

Al enfocarse en H(s) sin usar el retraso e^-3s se tiene H₁(s)

H_1(s) = \frac{3s+2}{(s+2)(s+1)}

y se usa el método de «cubrir» de Heaviside para encontrar las constantes,

k_1 = \frac{3s+2}{\cancel{(s+2)}(s+1)} \Big|_{s=-2} = \frac{3(-2)+2}{(-2+1)}=4

k_2 = \frac{3s+2}{(s+2)\cancel{(s+1)}} \Big|_{s=-1} = \frac{3(-1)+2}{(-1+2)} = -1

reemplazando las constantes en H₁(s) o mejor en H(s) se obtiene expresiones mas simples en fracciones parciales.

H(s) = \Big[ \frac{4}{s+2}- \frac{1}{s+1}\Big] e^{-3s}

H(s) = e^{-3s} \frac{4}{s+2} - e^{-3s}\frac{1}{s+1}

b. Usar la tabla de transformadas de Laplace, y la propiedad de desplazamiento en t

h(t) = 4e^{-2(t-3)}\mu(t-3)- e^{-(t-3)}\mu(t-3)

Tarea: usar la forma analítica para encontrar la respuesta.

la gráfica de respuesta del sistema ht(t) y la salida y(t) del sistema ante una entrada impulso, serán iguales:

c. ¿Qué puede decir acerca de la estabilidad interna y externa?

Los polos se encuentran en el lado izquierdo del plano, sus componentes son exponenciales decrecientes. Por lo que se considera asintóticamente estable, tambien es acotado o BIBO estable.

Estabilidad de H(s):
 n_polos_real : 2
 n_polos_imag : 0
 enRHP : 0
 unicos : 0
 repetidos : 0
 asintota : estable

revisando el resultado de los polos en conjunto con H(s)

Resultados con el algoritmo:

 H(s) = P(s)/Q(s):
/  4       1  \  -3*s
|----- - -----|*e    
\s + 2   s + 1/      
 H(s) en factores:
           -3*s
(3*s + 2)*e    
---------------
(s + 1)*(s + 2)

 h(t) :
/   3  -t      6  -2*t\                 
\- e *e   + 4*e *e    /*Heaviside(t - 3)

polosceros:
exp(-3*s) : {'Q_polos': {-1: 1, -2: 1}, 
             'P_ceros': {-2/3: 1}}
Q_polos : {-1: 1, -2: 1}
P_ceros : {-2/3: 1}

Estabilidad de H(s):
 n_polos_real : 2
 n_polos_imag : 0
 enRHP : 0
 unicos : 0
 repetidos : 0
 asintota : estable

 X(s): 
1

Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0

 ZSR respuesta estado cero:
ZSR :
/  4       1  \  -3*s
|----- - -----|*e    
\s + 2   s + 1/      
yt_ZSR :
/   3  -t      6  -2*t\                 
\- e *e   + 4*e *e    /*Heaviside(t - 3)

 Y(s)_total = ZIR + ZSR:
/  4       1  \  -3*s
|----- - -----|*e    
\s + 2   s + 1/      

 y(t)_total = ZIR + ZSR:
/   3  -t      6  -2*t\                 
\- e *e   + 4*e *e    /*Heaviside(t - 3)

Instrucciones en Python

Para resolver el ejercicio, se define la funcion H(s) por los polinomios P y Q, la entrada se define como un impulso δ(t).

Usando los bloques desarrollados en la Unidad 4 Sistemas LTI – Laplace y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta.

# Y(s) Respuesta total con entada cero y estado cero
# Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs
# http://blog.espol.edu.ec/telg1001/
import sympy as sym
import matplotlib.pyplot as plt
import telg1001 as fcnm

# INGRESO
s = sym.Symbol('s')
t = sym.Symbol('t', real=True)
d = sym.DiracDelta(t)
u = sym.Heaviside(t)

# H(s) y estabilidad
Hs = (3*s+2)/(s**2+3*s+2) * sym.exp(-3*s)
#Hs = 2*(s+5)/((s+4)*(s+3)) * sym.exp(-3*s)

# X(s) Señal de entrada
xt = d #+ d.subs(t,t-2)

# condiciones iniciales, [y'(0),y(0)] orden descendente
t0 = 0
cond_inicio = [0, 0] # estado cero no se usan

# Grafica, intervalo tiempo [t_a,t_b]
t_a = 0 ; t_b = 10
muestras = 101  # 51 resolucion grafica

# PROCEDIMIENTO
Hs = fcnm.apart_s(Hs) # fracciones parciales
Hs_fc = fcnm.factor_exp(Hs) # en factores
Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc)

polosceros = fcnm.busca_polosceros(Hs)
Q_polos = polosceros['Q_polos']
P_ceros = polosceros['P_ceros']

estable = fcnm.estabilidad_asintotica_s(Q_polos)

# H(t) respuesta al impulso
ht = 0*s
term_suma = sym.Add.make_args(Hs)
for term_k in term_suma:
    ht_k = sym.inverse_laplace_transform(term_k,s,t)
    # simplifica log(exp()) ej: e**(-2s)/(s**2)
    if ht_k.has(sym.log):
        ht_k = sym.simplify(ht_k,inverse=True)
    ht  = ht + ht_k
lista_escalon = ht.atoms(sym.Heaviside)
ht = sym.expand(ht,t) # terminos suma
ht = sym.collect(ht,lista_escalon)

# PROCEDIMIENTO Respuesta ZIR, ZSR
Xs = fcnm.laplace_transform_suma(xt)

# ZIR_s respuesta entrada cero de s
sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio)
ZIR = sol_ZIR['ZIR']
yt_ZIR = sol_ZIR['yt_ZIR']

# ZSR respuesta estado cero, Y(s) a entrada X(s)
sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs)
ZSR = sol_ZSR['ZSR']
yt_ZSR = sol_ZSR['yt_ZSR']

# Respuesta total Y(s) y y(t)
Ys = ZIR + ZSR
Ys = fcnm.apart_s(Ys)
yt = yt_ZIR + yt_ZSR
lista_escalon = yt.atoms(sym.Heaviside)
yt = sym.collect(yt,lista_escalon)

# SALIDA
print(' H(s) = P(s)/Q(s):')
sym.pprint(Hs)
print(' H(s) en factores:')
sym.pprint(Hs_fc)
if len(Hs_Qs2)>0:
    print('\nH(s) parámetros cuadraticos:')
    fcnm.print_resultado_dict(Hs_Qs2)

print('\n h(t) :')
sym.pprint(ht)

print('\npolosceros:')
fcnm.print_resultado_dict(polosceros)

print('\nEstabilidad de H(s):')
for k in estable:
    print('',k,':',estable[k])

print('\n X(s): ')
sym.pprint(Xs)
print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales')

if not(sol_ZIR == sym.nan): # existe resultado
    fcnm.print_resultado_dict(sol_ZIR)
else:
    print(' insuficientes condiciones iniciales')
    print(' revisar los valores de cond_inicio[]')

print('\n ZSR respuesta estado cero:')
fcnm.print_resultado_dict(sol_ZSR)

print('\n Y(s)_total = ZIR + ZSR:')
sym.pprint(Ys)
print('\n y(t)_total = ZIR + ZSR:')
sym.pprint(yt)

# Graficas polos, H(s), con polos h(t) --------
muestras_H = 101
figura_s  = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,f_nombre='H',solopolos=True)
figura_Hs = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,muestras=muestras_H,f_nombre='H')
figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h')
# GRAFICAS y(t),x(t),h(t) ---------------------
figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras)
plt.show()

Referencia: LTI CT Laplace – H(s) Estabilidad del sistema con Python
Ejemplo 3, LTI CT Laplace – H(s) Diagramas de bloques y ecuaciones diferenciales

1 agosto, 20174 febrero, 2023

Evaluaciones por temas

29 julio, 20174 febrero, 2023

Sigma-Delta – Modulación con Python

Referencia: Leon-Couch, 3–8 Modulación Delta, p.192 ; Delta-sigma_modulation Wikipedia

La modulación Sigma-Delta (∑Δ ) codifica una señal analógica a digital generando una secuencia de +1 y -1 (impulsos) que representan la diferencia entre la señal analógica muestreada y la señal digital acumulada. Tiene aplicaciones en sintetizadores de frecuencia, fuentes de poder conmutadas y controladores de motor.

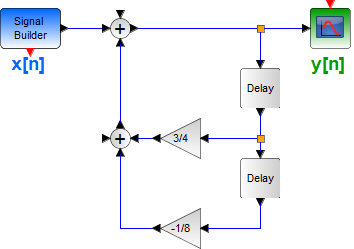
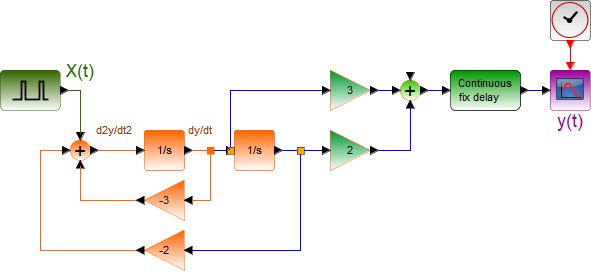
El sistema en diagrama de bloques en simulink se muestra en la figura:

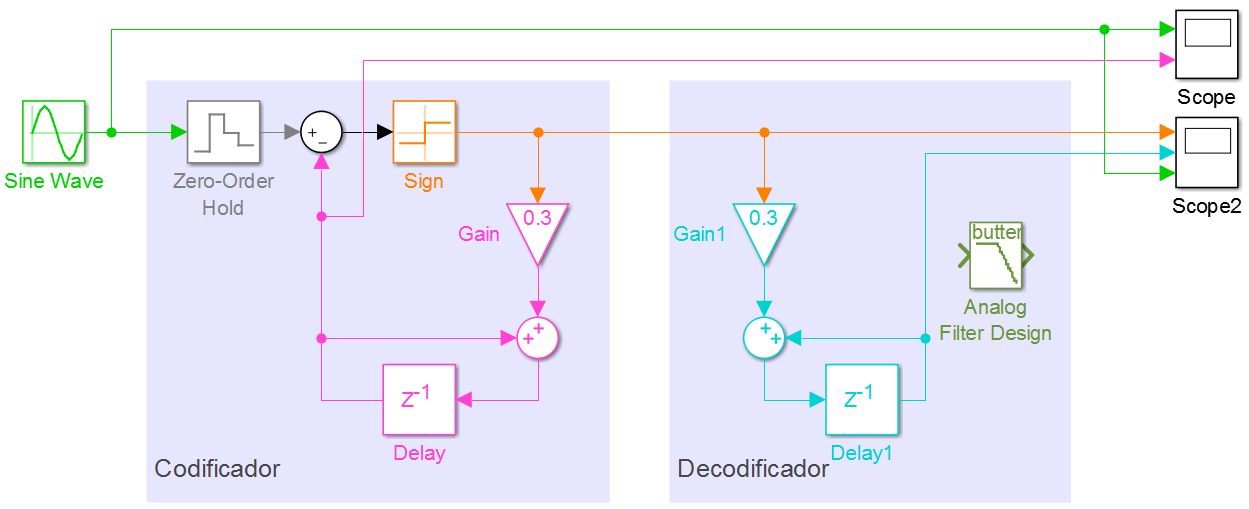
La señal de entrada (Sine Wave) se cuantifica en (Zero-Order Hold).

Luego se obtiene el signo (sign) de la diferencia entre la señal de entrada y la señal digital acumulada (∑) que genera la secuencia de +1 y -1 en la salida del codificador.

El valor de la ganancia Δ=0.3 representa el valor del escalón de subida o bajada de la señal digital acumulada, representada en color magenta.

La secuencia de salida +1 y -1, de nuevo acumulada en el decodificador, permite obtener una versión digital cercana a la señal analógica inicial.

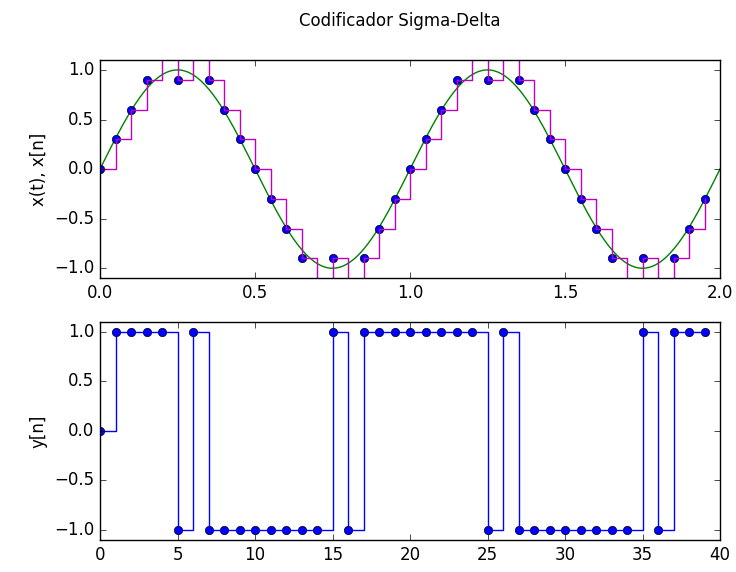
CODIFICADOR Sigma-Delta

La señal de entrada para el ejemplo tiene frecuencia fs=1 Hz, Δ=deltaY=0.3, rango [0,tn] hasta 2 segundos con divisiones k=40 en el rango de tiempo.

>>> 
rango [0,tn]:2
Secciones en el rango k:40
[ 0  1  1  1  1 -1  1 -1 -1 -1 -1 -1 -1 -1 -1
  1 -1  1  1  1  1  1  1  1  1 -1  1 -1 -1 -1
 -1 -1 -1 -1 -1  1 -1  1  1  1]
[  0.05   0.3   40.  ]

El script genera la gráfica y los archivos para datos y parámetros en formato texto.

La señal de entrada y los valores pueden ser modificados en el script adjunto:

# Modulacion Delta - Codificador
# entrada x(t), salida: y[n]
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt

# Definir la funcion de Entrada
def entradax(t,fs):
    x = np.sin(2*np.pi*fs*t)
    return(x)

# PROGRAMA para la modulación
# INGRESO
t0 = 0
tn = float(input('rango [0,tn]:'))
k  = int(input('Secciones en el rango k:'))

# PROCEDIMIENTO
# Analógica Referencia
fs = 1
m  = 500  # puntos en eje t para gráfico analógica
dm = (tn-t0)/m
t  = np.arange(0,tn,dm)  # eje tiempo analógica

xanalog = np.zeros(m, dtype=float)
for i in range(0,m):
    xanalog[i] = entradax(t[i],fs)

# Codificar Sigma-Delta
deltaY = 0.3          # Tamaño delta en eje Y
deltaT = (tn-t0)/k    # Tamaño delta en eje tiempo
td     = np.arange(0,tn,deltaT)    # tiempo muestreo
muestra  = np.zeros(k, dtype=float) # analógica para comparar
xdigital = np.zeros(k, dtype=float) # digital
ysalida  = np.zeros(k, dtype=int)   # Salida de +1|-1

td[0] = t0
muestra[0] = entradax(td[0],fs)
ysalida[0] = 0
for i in range(1,k):
    muestra[i] = entradax(td[i],fs) # referencia analógica
    diferencia = muestra[i]-xdigital[i-1]
    if (diferencia>0):
        bit = 1
    else:
        bit = -1
    xdigital[i] = xdigital[i-1]+bit*deltaY
    ysalida[i]  = bit
parametros = np.array([deltaT,deltaY,k])

# SALIDA
print(ysalida)
print(parametros)
np.savetxt('sigmadelta_datos.txt',ysalida,fmt='%i')
np.savetxt('sigmadelta_parametros.txt',parametros)

# Graficar
plt.figure(1)       # define la grafica
plt.suptitle('Codificador Sigma-Delta')

plt.subplot(211)    # grafica de 2x1 y subgrafica 1
plt.ylabel('x(t), x[n]')
xmax=np.max(xanalog)+0.1*np.max(xanalog) # rango en el eje y
xmin=np.min(xanalog)-0.1*np.max(xanalog)
plt.axis((t0,tn,xmin,xmax)) # Ajusta ejes
plt.plot(t,xanalog, 'g')
plt.axis((t0,tn,xmin,xmax))
plt.plot(td,xdigital,'bo')  # Puntos x[n]
plt.step(td,xdigital, where='post',color='m')

plt.subplot(212)    # grafica de 2x1 y subgrafica 2
plt.ylabel('y[n]')
plt.axis((0,k,-1.1,1.1))
plt.plot(ysalida, 'bo')     # Puntos y[n]
puntos = np.arange(0,k,1)     #posicion eje x para escalon
plt.step(puntos,ysalida, where='post')

plt.show()

Decodificador Sigma-Delta

Para observar el resultado, se decodifican los datos y se obtiene el siguiente resultado:

>>>
entrada: [ 0  1  1  1  1 -1  1 -1 -1 -1 -1 -1 -1 -1 -1
           1 -1  1  1  1  1  1  1  1  1 -1  1 -1 -1 -1
          -1 -1 -1 -1 -1  1 -1  1  1  1]
salida: 
[ 0.0000000e+00   3.0000000e-01   6.0000000e-01   9.0000000e-01
  1.2000000e+00   9.0000000e-01   1.2000000e+00   9.0000000e-01
  6.0000000e-01   3.0000000e-01  -1.1102230e-16  -3.0000000e-01
 -6.0000000e-01  -9.0000000e-01  -1.2000000e+00  -9.0000000e-01
 -1.2000000e+00  -9.0000000e-01  -6.0000000e-01  -3.0000000e-01
 -1.1102230e-16   3.0000000e-01   6.0000000e-01   9.0000000e-01
  1.2000000e+00   9.0000000e-01   1.2000000e+00   9.0000000e-01
  6.0000000e-01   3.0000000e-01  -1.1102230e-16  -3.0000000e-01
 -6.0000000e-01  -9.0000000e-01  -1.2000000e+00  -9.0000000e-01
 -1.2000000e+00  -9.0000000e-01  -6.0000000e-01  -3.0000000e-01]

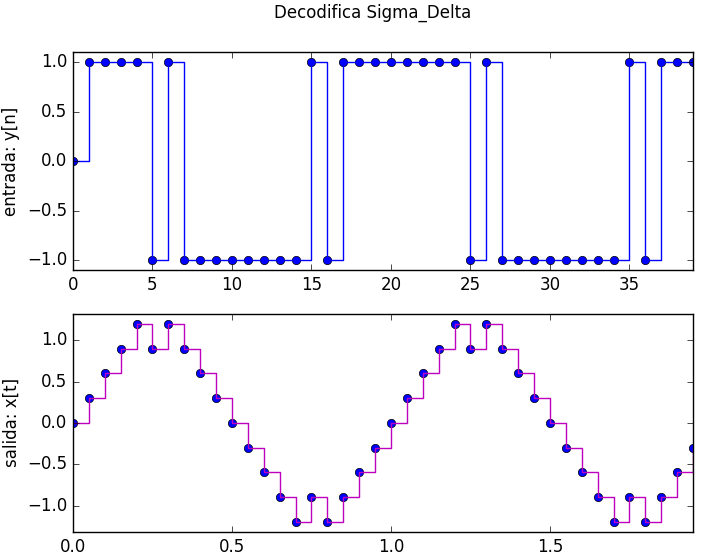
realizado usando el siguiente script de python:

# Modulacion Sigma-Delta Decodificador
#  entrada y[n], salida: x[n]
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
archivodatos = 'sigmadelta_datos.txt'
archivoparam = 'sigmadelta_parametros.txt'

# PROCEDIMIENTO
# Lectura de datos desde archivos
yentrada = np.loadtxt(archivodatos,dtype=int)
datos    = np.loadtxt(archivoparam,dtype=float)

deltaT = datos[0] # Tamaño delta en eje tiempo
deltaY = datos[1] # Tamaño delta en eje Y

# número de muestras
k = len(yentrada) 
xdigital = np.zeros(k, dtype=float)
punto    = np.zeros(k, dtype=int)   # número de muestra
td       = np.zeros(k, dtype=float) # tiempo muestreo

# DECOdifica Sigma-Delta
xdigital[0] = yentrada[0]
punto[0] = 0
td[0]    = 0
for i in range(1,k):
    punto[i] = i
    td[i]    = deltaT*i
    xdigital[i] = xdigital[i-1]+yentrada[i]*deltaY

# SALIDA
print('entrada:', yentrada)
print('salida:',xdigital,)

# Graficar
plt.figure(1)       # define la grafica
plt.suptitle('Decodifica Sigma_Delta')

plt.subplot(211)    # grafica de 2x1 y subgrafica 1
plt.ylabel('entrada: y[n]')
plt.axis((0,k-1,-1.1,1.1)) # Ajusta ejes
plt.plot(punto,yentrada,'bo') # Puntos y[n]
plt.step(punto,yentrada, where='post')

plt.subplot(212)    # grafica de 2x1 y subgrafica 2
plt.ylabel('salida: x[t]')
# rango en el eje y
xmax = np.max(xdigital)+0.1*np.max(xdigital)
xmin = np.min(xdigital)-0.1*np.max(xdigital)
plt.axis((0,td[k-1],xmin,xmax)) # Ajusta ejes
plt.plot(td,xdigital,'bo')
plt.step(td,xdigital, where='post', color='m')

plt.show()

Tarea

Realice observaciones cambiando:

a) la frecuencia de la señal de entrada,
b) el valor para deltaY
c) el rango tnd) el número de secciones en el tiempo
e) la forma de la señal de entrada a triangular, diente de sierra, exponencial periódica, etc.