Referencia: Lathi Ejercicio 1.8 p86, Oppenheim ejemplo 1.1 p10, Hsu problema 1.22 p35
Una señal compuesta que se construye con varias señales mas simples, que entre ellas se encuentran desplazadas, con cambios de escala en tiempo, etc. Para realizar la gráfica de la señal compuesta con Python se las escribe como la suma de las partes. También es posible usar la forma por partes piecewise() o como un conjunto de instrucciones por bloques.
En Python es necesario seleccionar la forma más conveniente para definir cada señal:
- en formato simplificado
lambda - por bloques
def-return
Por ejemplo Un escalón es mas sencillo definir en formato Lamba. Sin embargo, una señal con más partes se recomendaría realizarla por partes o bloques, definiendo su forma más básica para luego poder realizar cambios de escala o desplazamientos en el tiempo.
u = lambda t: np.heaviside(t,1)
Ejemplo 1. Señal compuesta
Referencia: Lathi Ejercicio 1.8 p86
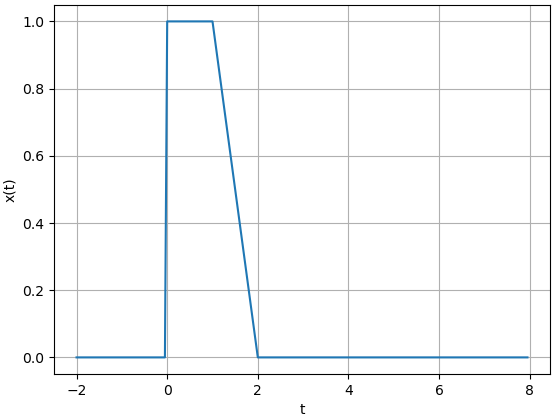
Demuestre que la señal mostrada en la figura (en libro y al final) puede ser descrita como:
x(t) = (t-1)\mu(t-1) - (t-2)\mu(t-2) - \mu(t-4)Instrucciones en Python
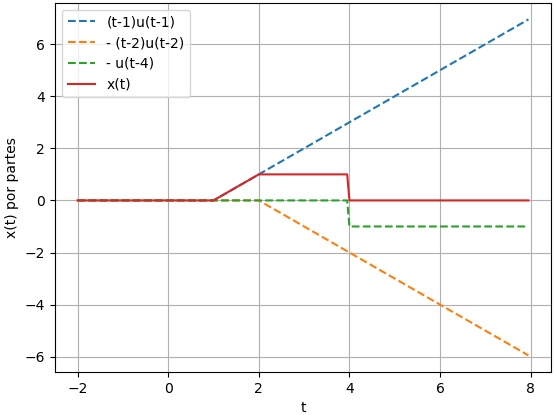
En el ejercicio se presenta que la señal se compone de la «suma» de sus partes. Se aprovecha la propiedad de linealidad para los sistemas para el caso presentado
# Señales modelo varias- ejercicio import numpy as np import matplotlib.pyplot as plt # INGRESO # u = lambda t: np.piecewise(t, t>=0, [1,0]) u = lambda t: np.heaviside(t,1) # señal como suma de las partes x1 = lambda t: (t-1)*u(t-1) x2 = lambda t: -(t-2)*u(t-2) x3 = lambda t: - u(t-4) x = lambda t: x1(t) + x2(t) + x3(t) # tiempo intervalo de observación a = -2 b = 8 dt = 0.05 # PROCEDIMIENTO ti = np.arange(a, b, dt) xi = x(ti) # evalua componentes para grafica x1i = x1(ti) x2i = x2(ti) x3i = x3(ti) # SALIDA - gráfico plt.figure(1) # componentes plt.plot(ti, x1i, '--', label='(t-1)u(t-1)') plt.plot(ti, x2i, '--', label='- (t-2)u(t-2)' ) plt.plot(ti, x3i, '--', label='- u(t-4)') plt.plot(ti, xi, label='x(t)') plt.legend() plt.ylabel('x(t) por partes') plt.xlabel('t') plt.grid() plt.figure(2) # señal compuesta plt.plot(ti, xi, label='x(t)') plt.ylabel('x(t)') plt.xlabel('t') plt.grid() plt.show()
Ejemplo 2. Señal compuesta
Referencia: Oppenheim ejemplo 1.1a p10
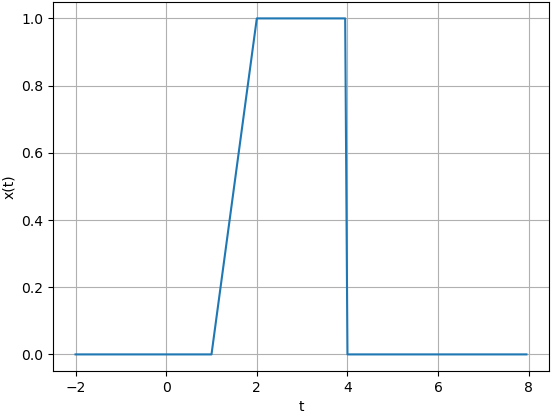
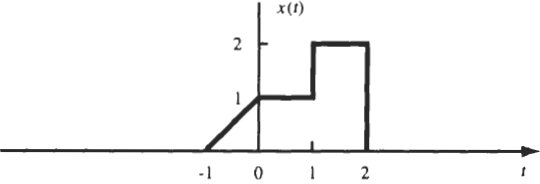
Dada la señal x(t) mostrada en la siguiente gráfica, realizar x(t+1), …
Procedemos como en el ejercicio anterior, continuando con el uso de la función escalón μ(t) .
# Señales modelo varias-ejercicio import numpy as np import matplotlib.pyplot as plt # INGRESO # u = lambda t: np.piecewise(t, t>=0, [1,0]) u = lambda t: np.heaviside(t,1) # señal como suma de las partes x1 = lambda t: -(t-1)*u(t-1) x2 = lambda t: (t-2)*u(t-2) x = lambda t: u(t) + x1(t) + x2(t) # tiempo intervalo de observación a = -2 b = 8 dt = 0.05 # PROCEDIMIENTO ti = np.arange(a, b, dt) xi = x(ti) # evalua componentes para grafica x0i = u(ti) x1i = x1(ti) x2i = x2(ti) # SALIDA - gráfico plt.figure(1) # componentes plt.plot(ti,x0i, '--', label='u(t)') plt.plot(ti,x1i, '--', label='-(t-1)*u(t-1)') plt.plot(ti,x2i, '--', label='(t-2)*u(t-2)') plt.plot(ti,xi, label='x(t)') plt.legend() plt.ylabel('x(t) por partes') plt.xlabel('t') plt.grid() plt.figure(2) # señal compuesta plt.plot(ti, xi, label='x(t)') plt.ylabel('x(t)') plt.xlabel('t') plt.grid() plt.show()
el resultado de la señal compuesta se observa en la gráfica
Ejercicio3. Señal con desplazamiento y escala
Referencia: Oppenheim ejemplo 1.1b p10
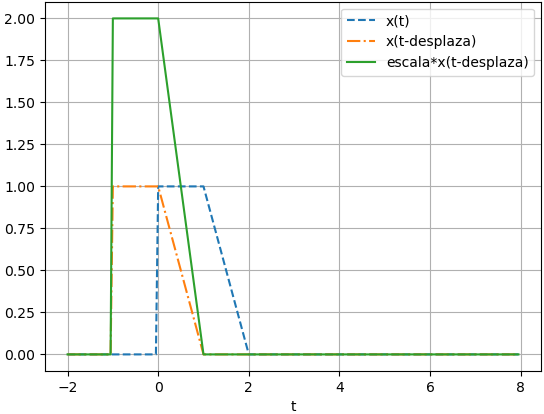
Semejante al ejercicio anterior, realizar la gráfica:
2x(t+1)Para el ejercicio, se define el punto donde se desplaza la señal, y la escala para la amplitud. Para observar los cambios se grafica el desplazamiento y luego el cambio de escala en magnitud.
# INGRESO desplaza = -1 escala = 2 xd_i = x(ti-desplaza) yi = escala*x(ti-desplaza) # salida - gráfico plt.figure(4) plt.plot(ti, xi, '--' , label='x(t)') plt.plot(ti, xd_i, '-.', label='x(t-desplaza)') plt.plot(ti, yi, label='escala*x(t-desplaza)') plt.xlabel('t') plt.legend() plt.grid() plt.show()
Tarea
Referencia: Oppenheim ejemplo 1.1a p10
A partir de la seña x(t) del ejercicio anterior, realice el ejercicio para obtener las gráficas:
- x(-t+1)
- x(3t/2)
- x(3t/2 +1)
Otros ejercicios
Referencia: Hsu problema 1.22 p35