1.7.1 Señales – Exponencial compleja

Referencia: Lathi 1.4-3 p89, Hsu 1.3.C p9, Oppenheim 1.3.1 p15 pdf46.

Exponencial e^st

Otra función importante en señales y sistemas es la señal e^st, donde s es en general de tipo compleja:

s = \sigma + j \omega

lo que convierte:

e^{st} =e^{( \sigma + j \omega)t} = e^{\sigma t} e^{j \omega t}

e^{st} =e^{\sigma t} \Big( \cos (\omega t) + j \sin (\omega t)\Big)

dado que la conjugada s^* = σ – jω

e^{s^* t} =e^{( \sigma - j \omega)t} = e^{\sigma t} e^{-j \omega t}

e^{s^* t} =e^{\sigma t} \Big( \cos (\omega t) - j \sin (\omega t)\Big)

por lo que sumando las ecuaciones resultantes anteriores:

e^{\sigma t} cos(\omega t) = \frac{1}{2}\Big( e^{st} + e^{s^{*}t} \Big)

Comparado con la formula de Euler, se muestra que e^st es una generalización de e^jω.

La función e^st tiene varias formas que pueden ser:

una constante k = e^st cuando s=0
una exponencial monótona e^σt cuando ω=0 y s=σ
una sinusoide cos (ωt) cuando σ=0 y s=±jω
una sinusoide con amplitud exponenial e^σt cos (ωt) cuando s=σ ±jω

Desarrollamos la gráfica del primer caso en Python, a partir de la cual repetimos el proceso para analizas los demas casos.

# Señales modelo varias
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
senal = lambda s,t: np.exp(s*t)
sigma = 0  # s = 0 +0j
omega = 0

a  = -5 # intervalo de tiempo [a,b)
b  = 5
dt = 0.1

# PROCEDIMIENTO
ti = np.arange(a, b, dt)
s_i = complex(sigma,omega)
senal_i = senal(s_i,ti)

# SALIDA - gráfica
plt.figure(1)
plt.plot(ti,np.real(senal_i),label='real')
plt.plot(ti,np.imag(senal_i),label='imaginaria')
plt.xlabel('t')
plt.ylabel('x(t)')
plt.legend()
plt.grid()
plt.title('e^('+str(sigma) +' + '+str(omega)+'j)')
plt.show()

A partir de aquí se continúa con la definición de t en el intervalo del ejercicio anterior, por lo que las instrucciones de Python se añaden a continuación de lo anterior.

Un exponencial simple σ>0 ω=0

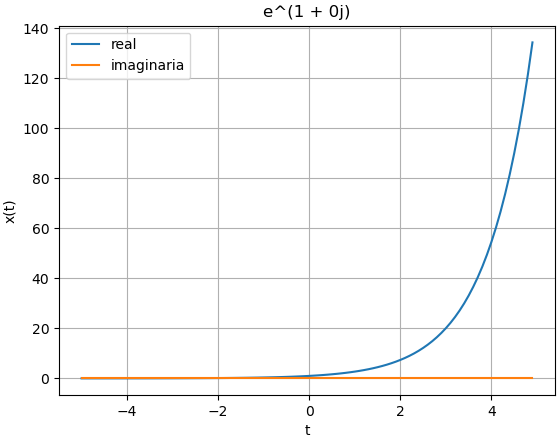Para éste caso se modifica en el bloque de ingreso los parámetros de σ=1 y ω=0, con lo que el algoritmo realiza la gráfica presentada.

# un exponencial simple sigma>0 omega=0 
sigma = 1
omega = 0

un exponencial simple σ<0 ω=0

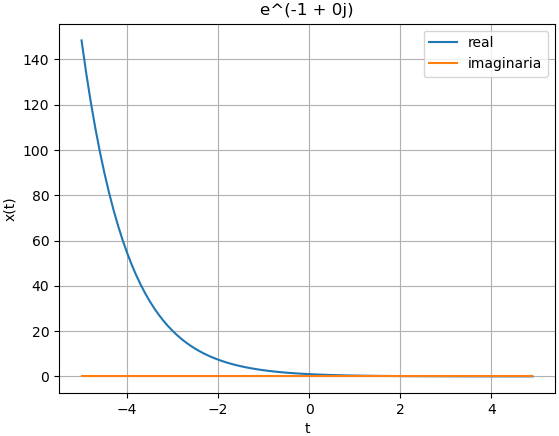
Para éste caso se modifica en el bloque de ingreso los parámetros de σ=-1 y ω=0, con lo que el algoritmo realiza la gráfica presentada.

# un exponencial simple sigma<0 omega=0
sigma = -1
omega = 0

un sinusiode σ=0, ω>0

Para éste caso se modifica en el bloque de ingreso los parámetros de σ=0 y ω=1, con lo que el algoritmo realiza la gráfica presentada.

# un sinusiode sigma=0, omega>0
sigma = 0
omega = 1

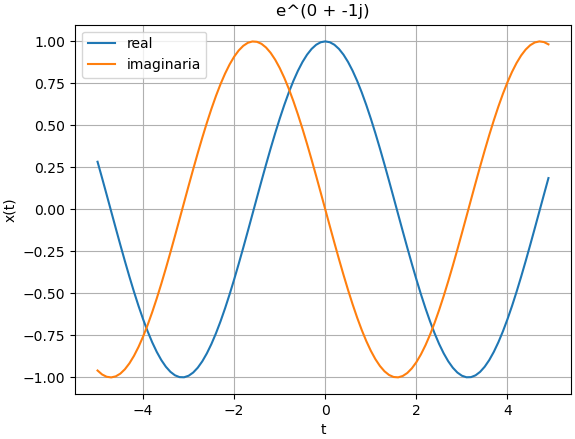
un sinusiode σ=0, ω<0

Para éste caso se modifica en el bloque de ingreso los parámetros de σ=0 y ω=-1, con lo que el algoritmo realiza la gráfica presentada.

# un sinusiode sigma=0, omega<0
sigma = 0
omega = -1

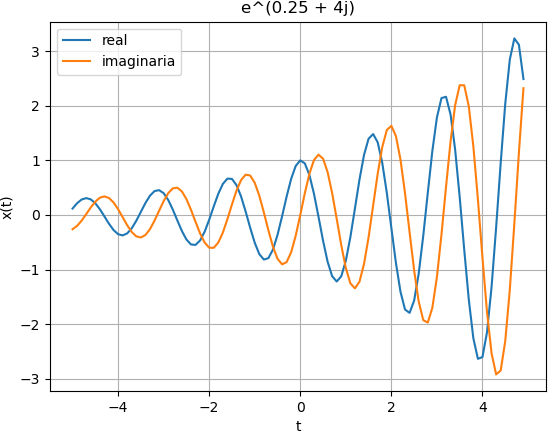
un sinusoide con amplitud exponencial σ=0.25, ω>0

# un sinusoide con amplitud exponencial sigma=0.25, omega>0
sigma = 0.25
omega = 4

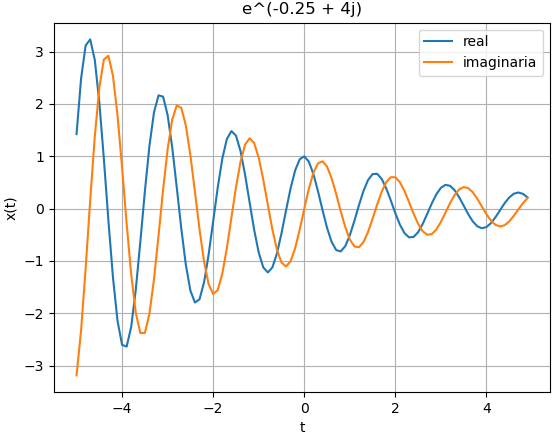
un sinusoide con amplitud exponencial σ=-0.25, ω>0

# un sinusoide con amplitud exponencial sigma=-0.25, omega>0
sigma = -0.25
omega = 4

Exponencial est