Referencia: Lathi 1.4.1 p83, Hsu 1.3 p6, Oppenheim 1.4 p30
[ escalón unitario ] [ impulso unitario ]
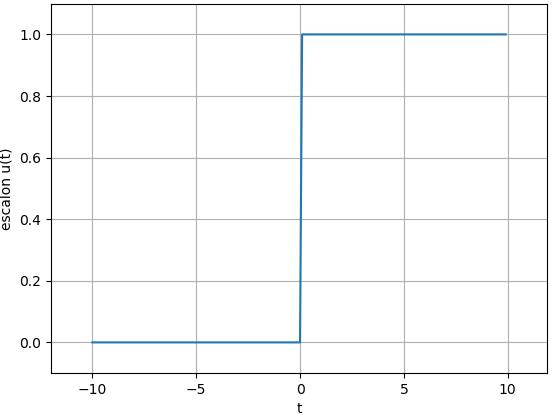
1. Escalón unitario μ(t)
Muchos de los temas de curso usan sistemas causales que inician en t=0. La función que describe éste comportamiento es escalón unitario μ(t) descrita como:
\mu(t)= \begin{cases} 1, & t\geq 0 \\ 0, & t<0\end{cases}Algunas señales pueden convenientemente ser descritas usando términos de una función μ(t) como se muestra en los siguientes ejemplos.
Instrucciones en Python
La función μ(t) se puede describir con la np.piecewise()o np.heaviside(t,1)
# Señales modelo varias import numpy as np import matplotlib.pyplot as plt # INGRESO #u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) a = -10 b = 10 dt = 0.1 # PROCEDIMIENTO ti = np.arange(a, b, dt) u0_i = u(ti) # SALIDA - GRAFICA print('t:',ti) print('t:',u0_i) # grafica plt.figure(1) plt.plot(ti,u0_i) plt.xlabel('t') plt.ylabel('escalon u(t)') plt.margins(dt) plt.grid() plt.show()
Señal Causal con Escalón unitario
Para convertir una señal cualquiera a causal, que inicie en t=0, se multiplica la señal por μ(t).
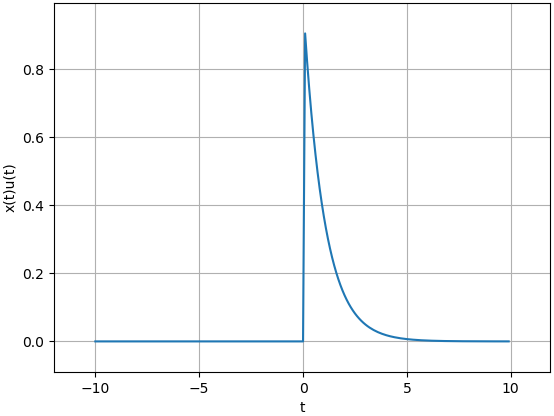
Por ejemplo, x(t)=e-αt se puede convertir a una señal causal si se escribe como:
x(t) = e^{-\alpha t} \mu(t)Para mostrar lo indicado y considerando α=1 tenemos que:
# señal a causal x = lambda t: np.exp(-t)*u(t) xi = x(ti) # SALIDA - GRAFICA plt.figure(2) plt.plot(ti,xi) plt.xlabel('t') plt.ylabel('x(t)u(t)') plt.margins(dt) plt.grid() plt.show()
La función escalón unitario también permite realizar descripciones matemáticas sobre diferentes segmentos del tiempo.
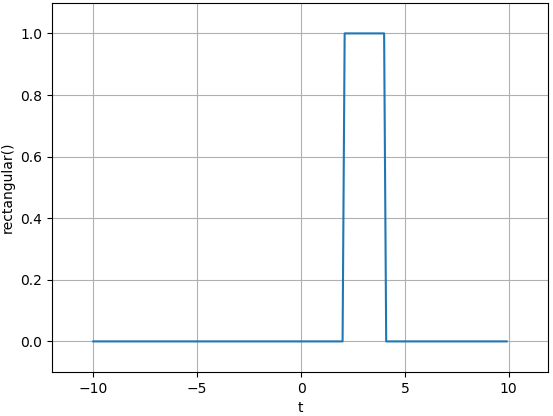
Señal Rectangular
Por ejemplo, una señal rectangular se puede representar como la suma de dos señales μ(t) desplazadas:
x(t) = \mu (t-2) - \mu (t-4)# Rectangular como u(t-2)-u(t-4) # u2 = lambda t: np.piecewise(t,t>=2,[1,0]) # u4 = lambda t: np.piecewise(t,t>=4,[1,0]) u2 = lambda t: u(t-2) u4 = lambda t: u(t-4) rectangular = lambda t:u2(t) - u4(t) rect_i = rectangular(ti) # SALIDA - GRAFICA plt.figure(3) plt.plot(ti,rect_i) plt.xlabel('t') plt.ylabel('rectangular(t)') plt.margins(dt) plt.grid() plt.show()
[ escalón unitario ] [ impulso unitario ]
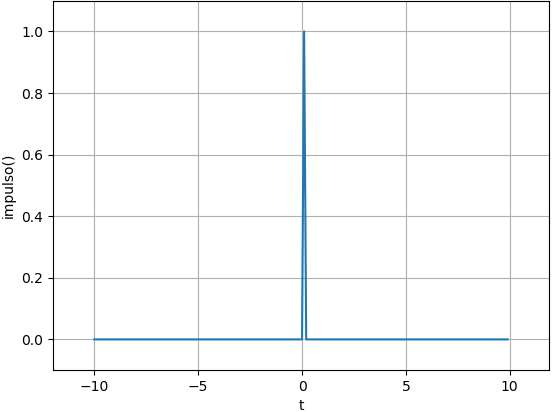
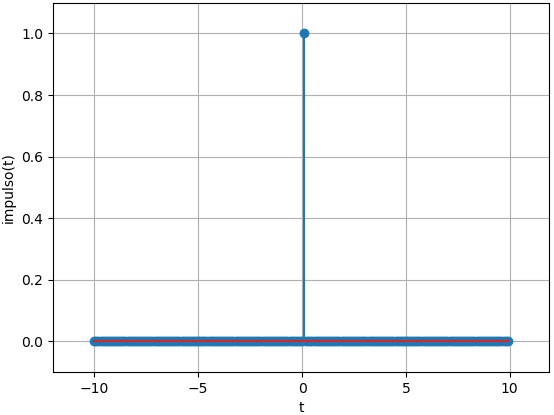
2. Impulso unitario δ(t)
El impulso unitario δ(t), delta de Dirac, es una función definida primero por Paul Dirac de la forma:
\delta(t)=0,t\neq 0 \int_{-\infty}^{\infty} \delta(t) dt = 1Se puede ver al impulso como un pulso rectangular muy pequeño de área unitaria. El ancho del pulso rectangular es muy pequeño.
Siguiendo el concepto, se puede representar como:
Instrucciones en Python
# Señales impulso unitario import numpy as np import matplotlib.pyplot as plt # INGRESO # u = lambda t: np.piecewise(t,t>=0,[1,0]) u = lambda t: np.heaviside(t,1) impulso = lambda t,dt: u(t)-u(t-dt) # intervalo de observación a = -10 b = 10 dt = 0.1 # tamaño de paso t0 = 0 # punto de impulso # PROCEDIMIENTO ti = np.arange(a, b, dt) impulso_i = impulso(ti,dt) # SALIDA - GRAFICA # plt.plot(ti,impulso_i) plt.stem(ti,impulso_i) plt.xlabel('t') plt.ylabel('impulso()') plt.grid() plt.show()
Otra forma de representar el impulso unitario es:
\delta(t)= \begin{cases} 1, & t = 0 \\ 0, & t \neq 0\end{cases}que como instrucción es,
impulso = lambda t,t0,tolera: 1*(np.abs(t-t0)<=tolera) t0 = 0 # punto de impulso tolera = 1e-10 # casicero
Para la gráfica también se usa stem(x,y):
# SALIDA - GRAFICA plt.figure(5) plt.stem(ti,impulso_i) plt.margins(dt) plt.xlabel('t') plt.ylabel('impulso(t)') plt.grid() plt.show()
También se puede usar la librería Scipy para tener un impulso más general:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.unit_impulse.html
hay que importar la librería Scipy para ese caso.