Ejercicio: 2Eva_IT2008_T1_MN Producción petroleo
Literal a
Para el cálculo de las derivadas se hace uso de las fórmulas de diferenciación presentadas en la unidad 6, y basadas en el polinomio de Taylor:
f'(x_i) = \frac{f(x_{i+1})-f(x_i)}{h} + O(h)
f''(x_i) = \frac{f(x_{i+2})-2f(x_{i+1})+f(x_i)}{h^2} + O(h)
[ dia, prod, dprod, d2prod]
[[ 1.000e+00 3.345e+03 -1.000e+02 6.600e+01]
[ 2.000e+00 3.245e+03 -3.400e+01 1.320e+02]
[ 3.000e+00 3.211e+03 9.800e+01 -5.600e+01]
[ 4.000e+00 3.309e+03 4.200e+01 1.900e+01]
[ 5.000e+00 3.351e+03 6.100e+01 -2.430e+02]
[ 6.000e+00 3.412e+03 -1.820e+02 8.700e+01]
[ 7.000e+00 3.230e+03 -9.500e+01 9.200e+01]
[ 8.000e+00 3.135e+03 -3.000e+00 0.000e+00]
[ 9.000e+00 3.132e+03 -3.000e+00 0.000e+00]
[ 1.000e+01 3.129e+03 0.000e+00 0.000e+00]]
representados en las siguientes gráfica:
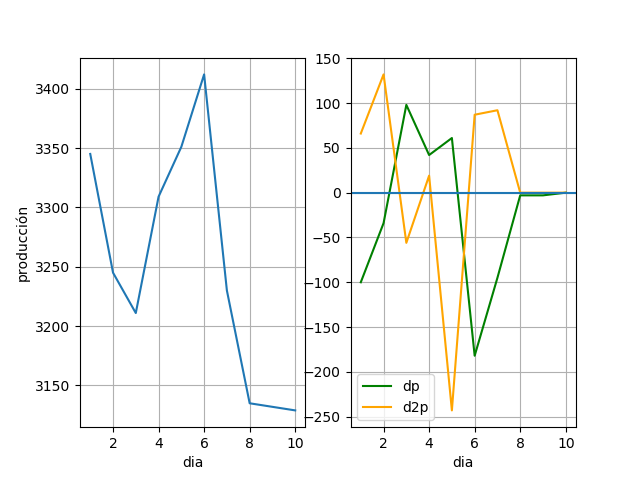
literal b
Dado que las fórmlas de error usadas tienen error del orden h: O(h), el error de las fórmulas es del orden de:
h= dia[1]-dia[0] = 2-1 = 1
literal c
Para el día dos se observa un decrecimiento en la producción, tal como lo refleja el valor negativo de la primera derivada.
Sin embargo para el día siguiente, la producción no mantiene la tasa de decrecimiento, se observa la segunda derivada positiva, Empieza a «acelerar».
Las instrucciones en Python para la tabla presentada son:
# 2Eva_IT2008_T1_MN Producción petroleo
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
dia = np.array( [1., 2, 3, 4, 5, 6, 7, 8, 9, 10])
produccion = [3345., 3245, 3211, 3309, 3351, 3412, 3230, 3135, 3132, 3129]
produccion = np.array(produccion, dtype = float)
# PROCEDIMIENTO
n = len(dia)
# primera derivada
dp = np.zeros(n,dtype=float)
for i in range(0,n-1,1):
dp[i] = (produccion[i+1]-produccion[i])/(dia[i+1]-dia[i])
# segunda derivada
d2p = np.zeros(n,dtype=float)
h = dia[1]-dia[0]
for i in range(0,n-2,1):
d2p[i] = (produccion[i]-2*produccion[i+1]+ produccion[i+2])/(h**2)
tabla = np.concatenate(([dia],[produccion],[dp],[d2p]),axis=0)
tabla = np.transpose(tabla)
# SALIDA
print(" [ dia, prod, dprod, d2prod]")
print(tabla)
# gráfica
plt.subplot(121)
plt.plot(dia,produccion)
plt.xlabel('dia')
plt.ylabel('producción')
plt.grid()
plt.subplot(122)
plt.plot(dia,dp,color='green',label='dp')
plt.xlabel('dia')
plt.plot(dia,d2p,color='orange',label='d2p')
plt.axhline(0)
plt.legend()
plt.grid()
plt.show()




