Ejercicio: 3Eva_2023PAOII_T3 Volumen por solido de revolución de un peón
El volumen se calcula a partir de la expresión:
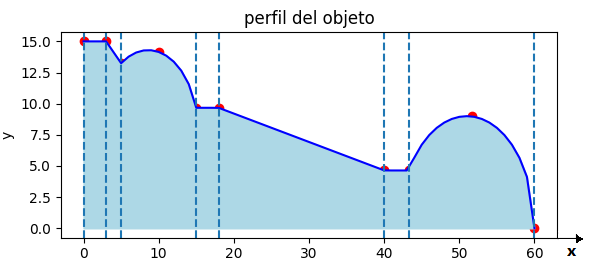
V = \int_{a}^{b} \pi (f(x))^2 dxxi=[ 0, 3, 5. , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60] yi=[15,15,13.25,14.1552, 9.6768, 9.67, 4.64, 4.64, 8.9768, 0.]
Para el intervalo [0,3]
La función es una constante
literal a, b y c
f(x) = 15 V = \int_{0}^{3} \pi (15)^2 dx = \pi (15)^2 x \big|_{0}^{3} = \pi (15)^2 (3-0) = 2120.5750Para el intervalo [3,5]
literal a
La función es una recta con pendiente negativa
f(x) = -0.875 x + 17.625 V = \int_{3}^{5} \pi (f(x))^2 dx V = \int_{3}^{5} \pi (-0.875 x+17.625)^2 dxpara el integral con cuadratura de Gauss
g(x) = \pi (-0.875*x+17.625)^2literal b y c
x_a = \frac{5+3}{2} - \frac{5-3}{2}\frac{1}{\sqrt{3}} = 3.4226 x_b = \frac{5+3}{2} + \frac{5-3}{2}\frac{1}{\sqrt{3}} = 4.5773con lo que el resultado aproximado del integral se convierte en:
I \cong \frac{5-3}{2}(g(3.4226) + g(4.5773)) = \frac{5-3}{2} (672.43+582.76) = 1255.1971Para el intervalo [5, 14.97]
literal a
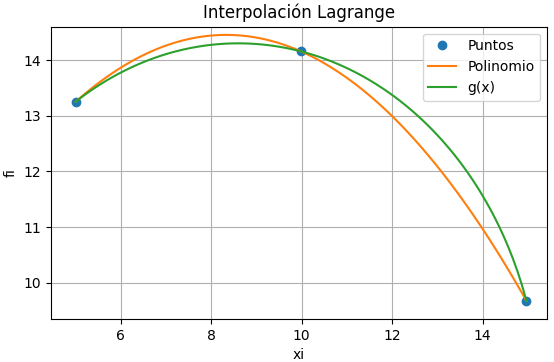
Del polinomio obtenido en el ejercicio anterior para éste intervalo
f(x) = -0.1083 x^2+1.8047 x + 6.9341 V = \int_{5}^{14.97} \pi (f(x))^2 dx V = \int_{5}^{14.97} \pi (-0.1083 x^2+1.8047 x + 6.9341)^2 dx [ g(x) = \pi (-0.1083 x^2+1.8047 x + 6.9341)^2literal b y c
x_a = \frac{14.97+5}{2} - \frac{14.97-5}{2}\frac{1}{\sqrt{3}} = 7.1069 x_b = \frac{14.97+5}{2} + \frac{14.97-5}{2}\frac{1}{\sqrt{3}} = 12.8630con lo que el resultado aproximado del integral se convierte en:
I \cong \frac{14.97-5}{2}(g(7.1069) + g(12.8630)) = \frac{14.97-5}{2} (641.5176+469.8124) = 5539.9805literal d
El volumen total es la suma de los resultados de cada una de las secciones:
V_{total} = 2120.5750 + 1255.1971 + 5539.9805 + ...Tarea: continuar con los otros intervalos para obtener el volumen total.
literal e
Resultados con el algoritmo
para f(x): [xa,xb]= [0.6339745962155612, 2.366025403784439] [f(xa),f(xb)]= [915.4418590078262, 760.106947830205] Volumenfx: 2513.323210257047 para f(x): [xa,xb]= [3.4226497308103743, 4.577350269189626] [f(xa),f(xb)]= [672.4334354361756, 582.7637293668464] Volumenfx: 1255.1971648030221 para f(x): [xa,xb]= [7.106908908089714, 12.863091091910285] [f(xa),f(xb)]= [641.5176069162055, 469.8124936184865] Volumenfx: 5539.98055116544
Instrucciones en Python
# 3Eva_2023PAOII_T3 Volumen por solido de revolución de un peón import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import axes3d # INGRESO # intervalos eje x, funciones #a=0 ; b=3 ; f = lambda x: np.pi*(15)**2 + 0*x #a=3 ; b=5 ; f = lambda x: np.pi*(-0.875*x+17.625)**2 # con el polinomio del tema 2 a=5 ; b=14.97 ; f = lambda x: np.pi*(-0.1083*x**2+1.8047*x + 6.9341)**2 # con el circulo del tema 1 #a=5 ; b=14.97 ; f = lambda x: np.pi*(np.sqrt(6.7**2-(x-8.6)**2) + 7.6)**2 xmuestras = 31 # PROCEDIMIENTO # Volumen para f(x) con Cuadratura de Gauss xa = (b+a)/2 + (b-a)/2*(-1/np.sqrt(3)) xb = (b+a)/2 + (b-a)/2*(1/np.sqrt(3)) Volumenfx = (b-a)/2*(f(xa)+f(xb)) xab = [xa,xb] fab = [f(xa),f(xb)] # SALIDA print("para f(x):") print("[xa,xb]=", xab) print("[f(xa),f(xb)]=", fab) print("Volumenfx: ",Volumenfx) print()
Añadir para graficar en 2D
# grafica 2D para el area de corte en eje y,x -------- # muestras en x xi = np.linspace(a, b, xmuestras) fi = f(xi) f0 = np.zeros(xmuestras,dtype=float) # grafica 2D figura2D = plt.figure() grafica2D = figura2D.add_subplot(111) grafica2D.plot(xi,fi,color='blue',label='f(x)') grafica2D.fill_between(xi,fi,f0,color='lightblue') grafica2D.grid() grafica2D.set_title('Area para sólido de revolución') grafica2D.set_xlabel('x') grafica2D.set_ylabel('f(x)')
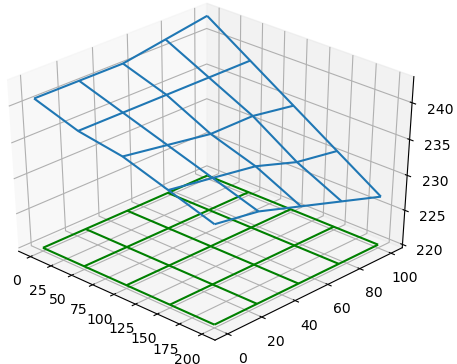
Añadir para graficar en 3D
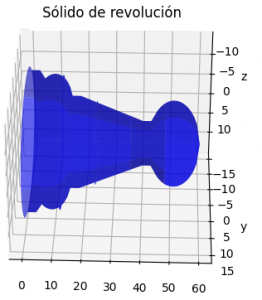
# Para grafica 3D ----------------------- # angulo w de rotación w_a = 0 w_b = 2*np.pi w_muestras = 31 # grafica 3D muestras en x y angulo w wi = np.linspace(w_a, w_b, w_muestras) X, W = np.meshgrid(xi, wi) # proyeccion en cada eje Yf = f(xi)*np.cos(W) Zf = f(xi)*np.sin(W) # grafica 3D figura3D = plt.figure() grafica = figura3D.add_subplot(111, projection='3d') grafica.plot_surface(X, Yf, Zf, color='blue', label='f(x)', alpha=0.6, rstride=6, cstride=12) grafica.set_title('Sólido de revolución') grafica.set_xlabel('x') grafica.set_ylabel('y') grafica.set_zlabel('z') # grafica.legend() eleva = 30 rota = -45 deltaw = 5 grafica.view_init(eleva, rota) # rotacion de ejes for angulo in range(rota, 360+rota, deltaw ): grafica.view_init(eleva, angulo) plt.draw() plt.pause(.001) plt.show()
.