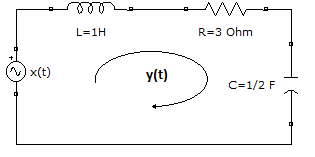
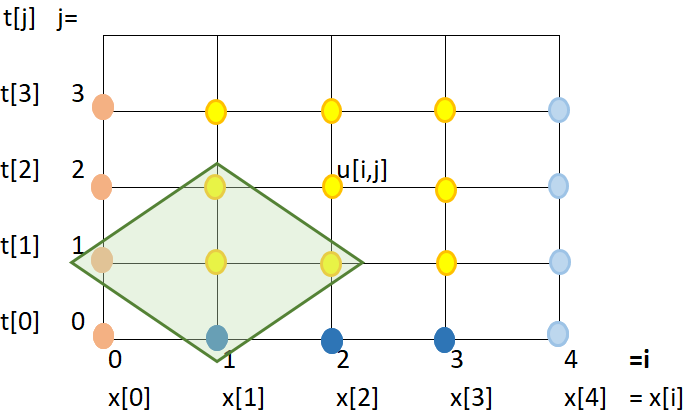
Referencia: Chapra 30.3 p893 pdf917, Burden 9Ed 12.2 p729, Rodriguez 10.2.4 p415
Para el ejercicio desarrollado en forma analítica como EDP Parabólicas método implícito, se desarrollan los pasos esta vez usando Sympy
\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}Las diferencias finitas centradas y hacia atras se definen en el diccionario dif_dividida.
Para cada valor de j, se crean las ecuaciones desde la forma discreta de la EDP, moviendo a la derecha los valores conocidos para generar un sistema de ecuaciones A.X=B. Se resuelve el sistema de ecuaciones y se actualiza la matriz u[i,j] de resultados.
EDP=0 :
2
d d
- K*--(u(x, t)) + ---(u(x, t)) = 0
dt 2
dx
Lambda L :
Dt
-----
2
Dx *K
discreta = 0 :
-2*U(i, j) + U(i - 1, j) + U(i + 1, j) K*(U(i, j) - U(i, j - 1))
-------------------------------------- - -------------------------
2 Dt
Dx
discreta_L = 0 :
L*U(i - 1, j) + L*U(i + 1, j) + (-2*L - 1)*U(i, j) + U(i, j - 1) = 0
Ecuaciones de iteraciones j:
j = 1
-1.5*U(1, 1) + 0.25*U(2, 1) = -40.0
0.25*U(1, 1) - 1.5*U(2, 1) + 0.25*U(3, 1) = -25.0
0.25*U(2, 1) - 1.5*U(3, 1) + 0.25*U(4, 1) = -25.0
0.25*U(3, 1) - 1.5*U(4, 1) + 0.25*U(5, 1) = -25.0
0.25*U(4, 1) - 1.5*U(5, 1) + 0.25*U(6, 1) = -25.0
0.25*U(5, 1) - 1.5*U(6, 1) + 0.25*U(7, 1) = -25.0
0.25*U(6, 1) - 1.5*U(7, 1) + 0.25*U(8, 1) = -25.0
0.25*U(7, 1) - 1.5*U(8, 1) + 0.25*U(9, 1) = -25.0
0.25*U(8, 1) - 1.5*U(9, 1) = -35.0
j = 2
-1.5*U(1, 2) + 0.25*U(2, 2) = -46.0050525095364
0.25*U(1, 2) - 1.5*U(2, 2) + 0.25*U(3, 2) = -26.0303150572187
0.25*U(2, 2) - 1.5*U(3, 2) + 0.25*U(4, 2) = -25.1768378337756
0.25*U(3, 2) - 1.5*U(4, 2) + 0.25*U(5, 2) = -25.030711945435
0.25*U(4, 2) - 1.5*U(5, 2) + 0.25*U(6, 2) = -25.0074338388344
0.25*U(5, 2) - 1.5*U(6, 2) + 0.25*U(7, 2) = -25.0138910875712
0.25*U(6, 2) - 1.5*U(7, 2) + 0.25*U(8, 2) = -25.0759126865931
0.25*U(7, 2) - 1.5*U(8, 2) + 0.25*U(9, 2) = -25.4415850319874
0.25*U(8, 2) - 1.5*U(9, 2) = -37.5735975053312
j = 3
-1.5*U(1, 3) + 0.25*U(2, 3) = -50.2512763902537
0.25*U(1, 3) - 1.5*U(2, 3) + 0.25*U(3, 3) = -27.4874483033763
0.25*U(2, 3) - 1.5*U(3, 3) + 0.25*U(4, 3) = -25.5521532011296
0.25*U(3, 3) - 1.5*U(4, 3) + 0.25*U(5, 3) = -25.1181195682987
0.25*U(4, 3) - 1.5*U(5, 3) + 0.25*U(6, 3) = -25.0337164269226
0.25*U(5, 3) - 1.5*U(6, 3) + 0.25*U(7, 3) = -25.0544436378994
0.25*U(6, 3) - 1.5*U(7, 3) + 0.25*U(8, 3) = -25.2373810501889
0.25*U(7, 3) - 1.5*U(8, 3) + 0.25*U(9, 3) = -26.0661919168616
0.25*U(8, 3) - 1.5*U(9, 3) = -39.3934303230311
j = 4
-1.5*U(1, 4) + 0.25*U(2, 4) = -53.3449104170748
0.25*U(1, 4) - 1.5*U(2, 4) + 0.25*U(3, 4) = -29.0643569414341
0.25*U(2, 4) - 1.5*U(3, 4) + 0.25*U(4, 4) = -26.0914380180247
0.25*U(3, 4) - 1.5*U(4, 4) + 0.25*U(5, 4) = -25.2756583621956
0.25*U(4, 4) - 1.5*U(5, 4) + 0.25*U(6, 4) = -25.0900338819544
0.25*U(5, 4) - 1.5*U(6, 4) + 0.25*U(7, 4) = -25.1296792218401
0.25*U(6, 4) - 1.5*U(7, 4) + 0.25*U(8, 4) = -25.4702668974885
0.25*U(7, 4) - 1.5*U(8, 4) + 0.25*U(9, 4) = -26.7423979623353
0.25*U(8, 4) - 1.5*U(9, 4) = -40.7193532090766
Solución u:
[[60. 60. 60. 60. 60. ]
[25. 31.00505251 35.25127639 38.34491042 40.6652135 ]
[25. 26.03031506 27.4874483 29.06435694 30.61163935]
[25. 25.17683783 25.5521532 26.09143802 26.74719483]
[25. 25.03071195 25.11811957 25.27565836 25.50577757]
[25. 25.00743384 25.03371643 25.09003388 25.18483712]
[25. 25.01389109 25.05444364 25.12967922 25.24310963]
[25. 25.07591269 25.23738105 25.4702669 25.75510376]
[25. 25.44158503 26.06619192 26.74239796 27.40644533]
[25. 27.57359751 29.39343032 30.71935321 31.71397636]
[40. 40. 40. 40. 40. ]]
>>>
Instrucciones en Python
El desarrollo de la ecuación en forma discreta se realizó en EDP Parabólica método explícito – analítico con Sympy-Python, por lo que se incorpora a éste algoritmo como una función, desde donde se inicia los parsos para el método implicito.
Compare los resultados con el método numérico y mida los tiempos de ejecución de cada algoritmo para escribir sus observaciones.
# Ecuaciones Diferenciales Parciales Parabólicas # método implícito con Sympy import numpy as np import sympy as sym # variables continuas t = sym.Symbol('t',real=True) x = sym.Symbol('x',real=True) u = sym.Function('u')(x,t) K = sym.Symbol('K',real=True) # variables discretas i = sym.Symbol('i',integer=True,positive=True) j = sym.Symbol('j',integer=True,positive=True) Dx = sym.Symbol('Dx',real=True,positive=True) Dt = sym.Symbol('Dt',real=True,positive=True) L = sym.Symbol('L',real=True) U = sym.Function('U')(i,j) # INGRESO # ecuacion: LHS=RHS LHS = sym.diff(u,x,2) RHS = K*sym.diff(u,t,1) EDP = sym.Eq(LHS-RHS,0) dif_dividida ={sym.diff(u,x,2): (U.subs(i,i-1)-2*U+U.subs(i,i+1))/(Dx**2), sym.diff(u,t,1): (U - U.subs(j,j-1))/Dt} # parametros Ta = 60 ; Tb = 40 ; T0 = 25 K_ = 4 x_a = 0 ; x_b = 1 x_tramos = 10 t_a = 0 # t_b depende de t_tramos y dt t_tramos = 4 dx = (x_b-x_a)/x_tramos dt = dx/10 L_k = dt/(dx**2)/K_ # PROCEDIMIENTO def edp_discreta(EDP,dif_dividida): ''' EDP contínua y diferencias divididas a usar ''' desarrollo={} # expresión a la izquierda LHS (Left Hand side) if EDP.rhs!=0: LHS = EDP.lhs RHS = EDP.rhs EDP = sym.Eq(LHS-RHS,0) desarrollo['EDP=0'] = EDP lamb = Dt/K/(Dx**2) desarrollo['Lambda L'] = lamb discreta = EDP.lhs # EDP discreta for derivada in dif_dividida: discreta = discreta.subs(derivada,dif_dividida[derivada]) desarrollo['discreta = 0'] = discreta # simplifica con lambda L discreta_L = sym.expand(discreta*Dt/K) discreta_L = discreta_L.subs(Dt/K/(Dx**2),L) discreta_L = sym.collect(discreta_L,U) discreta_L = sym.Eq(discreta_L,0) desarrollo['discreta_L = 0'] = discreta_L return(desarrollo) edp_discreta = edp_discreta(EDP,dif_dividida) # u[x,t] resultados, valores iniciales xi = np.arange(x_a,x_b+dx,dx) ti = np.arange(t_a,t_a+t_tramos*dt+dt,dt) uxt = np.zeros(shape=(x_tramos+1,t_tramos+1), dtype=float) uxt = uxt*np.nan uxt[0,:] = Ta uxt[1:x_tramos+1,0] = T0 uxt[x_tramos,:] = Tb # EDP parabólicas método implícito # conoce valor de uxt[i,j] conoce = np.zeros(shape=(x_tramos+1,t_tramos+1), dtype=bool) conoce[:,0] = 1 # inferior conoce[0,:] = 1 # izquierda conoce[-1,:] = 1 # derecha # ecuaciones por iteracion j eq_itera = [] for jk in range(1,t_tramos+1,1): eq_jk = [] for ik in range(1,x_tramos,1): LHS = edp_discreta['discreta_L = 0'].lhs RHS = 0*t LHS = LHS.subs([(i,ik),(j,jk),(L,L_k)]) # revisa terminos de suma term_suma = sym.Add.make_args(LHS) for term_k in term_suma: cambiar = False cambiar_valor = 0 ; cambiar_factor = 0 # revisa factores en termino de suma factor_Mul = sym.Mul.make_args(term_k) for factor_k in factor_Mul: if factor_k.is_Function: # es U(i,j) [i_k,j_k] = factor_k.args cambiar = conoce[i_k,j_k] cambiar_factor = factor_k cambiar_valor = uxt[i_k,j_k] # U(i,j)conocidos pasan a la derecha if cambiar: RHS = RHS-term_k RHS = RHS.subs(cambiar_factor, cambiar_valor) LHS = LHS-term_k # agrupa ecuaciones de iteración i eq_jk.append(sym.Eq(LHS,RHS)) # resuelve sistema ecuaciones A.X=B X_jk = sym.solve(eq_jk)[0] # actualiza uxt(i,j) , conoce[i,j] for nodoij in X_jk: [i_k,j_k] = nodoij.args uxt[i_k,j_k] = X_jk[nodoij] conoce[i_k,j_k] = True # agrupa ecuaciones por cada j eq_itera.append(eq_jk) # SALIDA for k in edp_discreta: print('\n',k,' :') sym.pprint(edp_discreta[k]) print('\nEcuaciones de iteraciones j:') for jk in range(0,t_tramos,1): print(' j =',jk+1) for una_eq in eq_itera[jk]: sym.pprint(una_eq) print('\nSolución u:') print(uxt)