Ejercicio: 1Eva_2024PAOI_T3 Tasas de natalidad en países desarrollados
Los datos de la tabla que se requieren usar para la tabla son los años 1965, 1980, 1995 y 2010.
| tasa | 7.32 | 4.89 | 3.50 | 2.79 |
| año | 1965 | 1980 | 1995 | 2010 |
| k | 0 | 3 | 6 | 9 |
literal a
Para cuatro datos o muestras el grado del polinomio que se puede plantear es 3. La ecuación se ordena siguiendo el modelo para la matriz de Vandermonde, primer coeficiente es del termino de mayor grado.
p(x) = ax^3+bx^2+cx+dPor el orden de magnitud del eje x comparado con los valores de las constantes, se usan los valores del vector k que corresponde a los índices de la tabla. El valor del año se obtiene al hacer un cambio de escala que inicia en el año t0 = 1965 y tamaño de paso Δx = 5 años.
el sistema de ecuaciones usando cada punto será:
p(0) = a(0)^3+b(0)^2+c(0)+d = 7.32 p(3) = a(3)^3+b(3)^2+c(3)+d = 4.89 p(6) = a(6)^3+b(6)^2+c(6)+d = 3.50 p(9) = a(9)^3+b(9)^2+c(9)+d = 2.79literal b
El sistema de ecuaciones para la Matriz de Vandermonde D y el vector de constantes B en la forma de matriz aumentada D|B:
\left[ \begin{array}{cccc | c} (0)^3 & (0)^2 & (0) & 1 & 7.32 \\ (3)^3 & (3)^2 & (3) &1 &4.89\\ (6)^3 & (6)^2 & (6) &1 & 3.50 \\ (9)^3 & (9)^2 & (9) & 1 & 2.79 \end{array} \right]literal c
Resolviendo el sistema de ecuaciones con el algoritmo y usando la instrucción np.linalg.solve(A,B)
>>> np.linalg.solve(A,B)
array([-2.22222222e-03, 7.77777778e-02,
-1.02333333e+00, 7.32000000e+00])
literal d
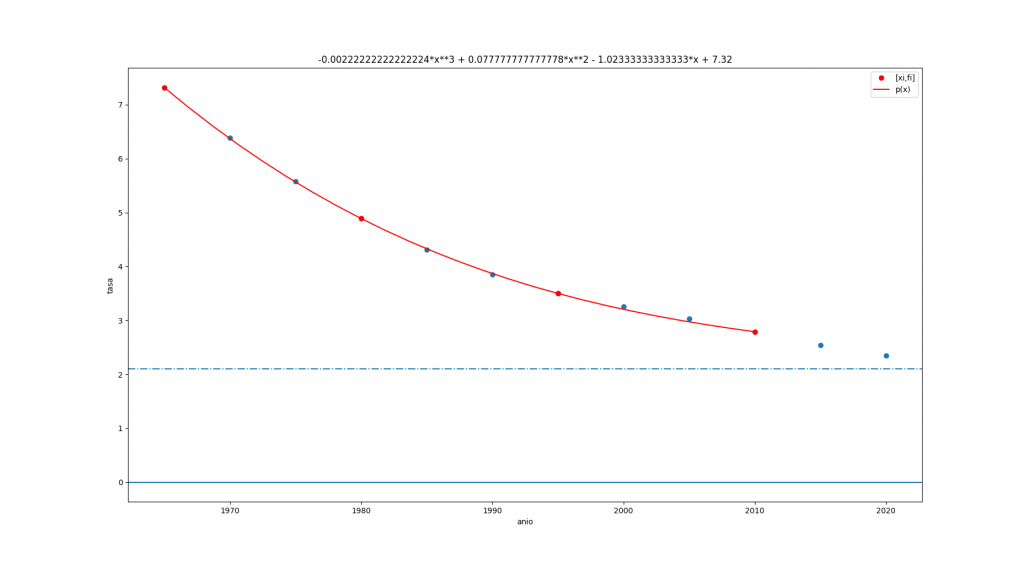
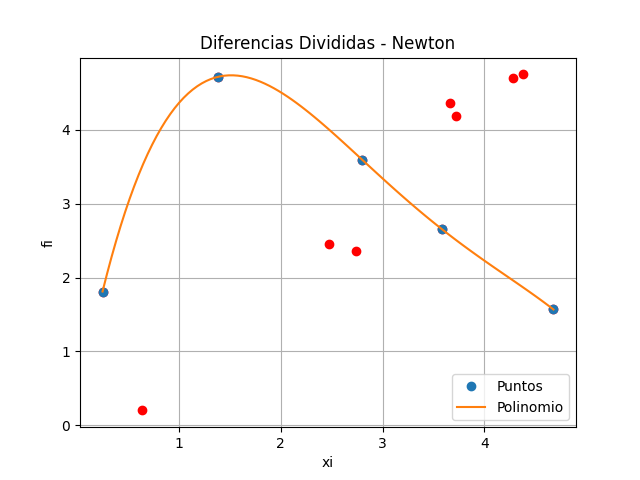
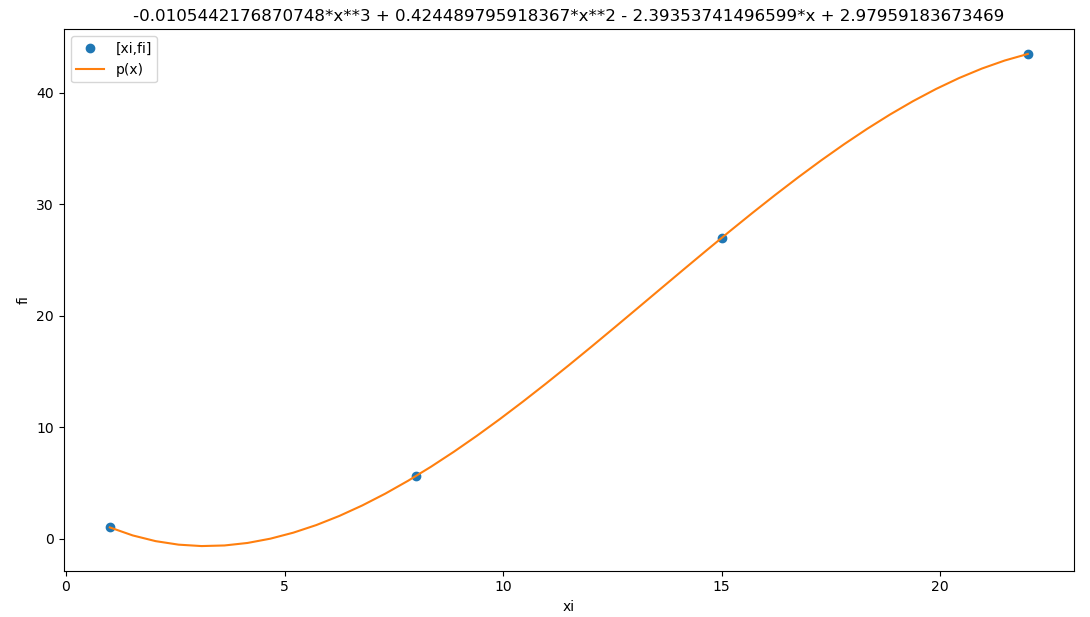
p(x) = -0.00222 x^3 + 0.07777 x^2 - 1.0233 x + 7.32Para el ajuste de escala de años, se usa:
año = x*5 +1965la gráfica usando el algoritmo, muestra que el polinomio pasa por los puntos seleccionados y existe un error entre los puntos que no participan en la construcción del polinomio.
literal e
El año 2020 en x se escala como
2020 = x*5 +1965x = 11
o revisando la tabla proporcionada en el ejercicio
p(11) = -0.00222 (11)^3 + 0.07777(11)^2 - 1.0233 (11)x + 7.32 = 2.5166el error se calcula usando el valor medido para el año 2020
error = | 2.51- 2.35| = 0.16literal f
p(x) = -0.00222 x^3 + 0.07777 x^2 - 1.0233 x + 7.32 = 2.51para resolverlo se requiere usar cualquiera de los algoritmos de la unidad 2.
>>> import scipy.optimize as opt >>> opt.bisect(px,11,30,xtol=0.001) 20.312713623046875 >>>
que corresponde al año = 20.31*5+1965 = 2066.55
Sin embargo la interpolación se usa para estimar valores dentro del intervalo de muestras. El concepto de extrapolación corresponde a otro capítulo. Sin embargo la pregunta se la considera para evaluar la comprensión de la unidad 2.
Algoritmo con Python
El resultado con el algoritmo se observa como
xi [0 3 6 9]
fi [7.32 4.89 3.5 2.79]
Matriz Vandermonde:
[[ 0. 0. 0. 1.]
[ 27. 9. 3. 1.]
[216. 36. 6. 1.]
[729. 81. 9. 1.]]
los coeficientes del polinomio:
[-2.22222222e-03 7.77777778e-02
-1.02333333e+00 7.32000000e+00]
Polinomio de interpolación:
-0.00222222224*x**3 + 0.077777778*x**2 - 1.02333333*x + 7.32
formato pprint
3 2
- 0.002222222224*x + 0.0777777778*x - 1.023333333*x + 7.32
>>> px(11)
2.5166666666667066
Instrucciones en Python
# 1Eva_2024PAOI_T3 Tasas de natalidad en países desarrollados import numpy as np import matplotlib.pyplot as plt import sympy as sym # INGRESO tasa = [7.32, 6.39, 5.58, 4.89,4.31,3.85,3.50,3.26,3.03,2.79,2.54,2.35] anio = [1965, 1970, 1975, 1980,1985,1990,1995,2000,2005,2010,2015,2020] k = [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11] cual = [0,3,6,9] tasamin = 2.1 # PROCEDIMIENTO fi = np.take(tasa,cual) xi = np.take(k,cual) # El polinomio de interpolación # muestras = tramos+1 muestras = 25 # PROCEDIMIENTO # Convierte a arreglos numpy xi = np.array(xi) B = np.array(fi) n = len(xi) # Matriz Vandermonde D D = np.zeros(shape=(n,n),dtype =float) for i in range(0,n,1): for j in range(0,n,1): potencia = (n-1)-j # Derecha a izquierda D[i,j] = xi[i]**potencia # Aplicar métodos Unidad03. Tarea # Resuelve sistema de ecuaciones A.X=B coeficiente = np.linalg.solve(D,B) # Polinomio en forma simbólica x = sym.Symbol('x') polinomio = 0 for i in range(0,n,1): potencia = (n-1)-i # Derecha a izquierda termino = coeficiente[i]*(x**potencia) polinomio = polinomio + termino # Polinomio a forma Lambda # para evaluación con vectores de datos xin px = sym.lambdify(x,polinomio) # Para graficar el polinomio en [a,b] a = np.min(xi) b = np.max(xi) xin = np.linspace(a,b,muestras) yin = px(xin) # SALIDA print('xi', xi) print('fi',fi) print('Matriz Vandermonde: ') print(D) print('los coeficientes del polinomio: ') print(coeficiente) print('Polinomio de interpolación: ') print(polinomio) print('\n formato pprint') sym.pprint(polinomio) # Grafica plt.plot(anio,tasa,'o') plt.plot(xi*5+anio[0],fi,'o',color='red', label='[xi,fi]') plt.plot(xin*5+anio[0],yin,color='red', label='p(x)') plt.xlabel('xi') plt.ylabel('fi') plt.legend() plt.axhline(0) plt.axhline(2.1,linestyle='-.') plt.xlabel('anio') plt.ylabel('tasa') plt.title(polinomio) plt.show()