3ra Evaluación – Métodos numéricos

2024-09-182024-09-18

3Eva_2024PAOI_T3 Salto Bungee y método de Jacobi

3ra Evaluación 2024-2025 PAO I. 17/Septiembre/2024

Tema 3. (35 puntos) Para el salto del Bungee y la tabla del ejercicio del tema 2, realice el sistema de ecuaciones para el polinomio de interpolación usando los tiempos en el vector t_s = [0, 0.75,1.375, 2.55]

datos usando h=1/8
ti	vi
0	0.0000
0.25	2.4479
0.5	4.8849
0.75	7.3001
1	9.6832
1.375	13.1763
1.75	16.5451
2.125	19.7641
2.4	22.0193
2.55	23.2075

Plantee el sistema de ecuaciones usando los cuatro puntos datos en el vector t_s
Presente el sistema de ecuaciones en su forma matricial y muestre la matriz aumentada y pivoteada
Desarrolle el ejercicio usando el método de Jacobi, para tres iteraciones. Justifique el vector inicial X₀
Comente sobre la convergencia del ejercicio y adjunte los archivos para algoritmo.py y resultados.txt

Rúbrica: Planteamiento (5 puntos), Matriz aumentada y pivoteada (5 puntos), iteraciones(15 puntos), error por iteración (5 puntos), literal d (5 puntos)

2024-09-182024-09-18

3Eva_2024PAOI_T2 Salto Bungee interpolar velocidad primer tramo

3ra Evaluación 2024-2025 PAO I. 17/Septiembre/2024

Tema 2. (30 puntos)
Para el salto del Bungee del ejercicio del tema anterior se toman lecturas con un sensor de velocidad sujetado a la persona.

De la tabla de datos obtenida, se observa que los tamaños de paso en tiempo no siempre son equidistantes.
Se requiere encontrar un polinomio interpolación de al menos grado 3.

datos usando h=1/8
ti	vi
0	0.0000
0.25	2.4479
0.5	4.8849
0.75	7.3001
1	9.6832
1.375	13.1763
1.75	16.5451
2.125	19.7641
2.4	22.0193
2.55	23.2075

a. Describa el planteamiento del ejercicio, selección de puntos, expresiones usando el método de Lagrange.

b. Resuelva el sistema usando los algoritmos correspondientes.

c. Presente el polinomio obtenido, simplificado y grafique verificando que P(x) pase por los puntos de muestra.

d. Use el resultado P(x) para estimar el error con los valores de vi que no fueron usados para la interpolación.

e. Adjunte los archivos para algoritmo.py, resultados.txt y grafica.png

Rúbrica: literal a (10 puntos), literal b (5 puntos), literal c (5 puntos), literal d (5 puntos), literal e (5 puntos)

Referencia: Chapra. capítulo 28. Ejercicio 28.41 p852.

2024-09-182024-09-18

3Eva_2024PAOI_T1 EDO Salto Bungee extiende y estira toda la cuerda

3ra Evaluación 2024-2025 PAO I. 17/Septiembre/2024

Tema 1. (35 puntos)
La ecuación diferencial para la velocidad de alguien que practica el salto del bungee es diferente según si el saltador ha caído una distancia en la que la cuerda está extendida por completo y comienza a estirarse o encogerse.

Si la distancia recorrida es menor que la longitud de la cuerda, el saltador sólo está sujeto a las fuerzas gravitacional y de arrastre de la cuerda.

\frac{d^2y}{dt^2} = g - signo(v) \frac{C_d}{m}\Big( \frac{dy}{dt}\Big)^2

y \leq L

Suponga que las condiciones iniciales son:

y(0) =0

\frac{dy(0)}{dt} = 0

Una vez que la cuerda comienza a estirarse, también deben incluirse las fuerzas del resorte y del amortiguamiento de la cuerda.

\frac{d^2y}{dt^2} = g - signo(v) \frac{C_d}{m}\Big( \frac{dy}{dt}\Big)^2 -\frac{k}{m}(y-L) - \frac{\gamma}{m}( \frac{dy}{dt}\Big)

y \gt L

dy/dt	m/s	velocidad (v)
t	s	tiempo
g	9.8 m/s²	gravedad
c_d	0.25 kg/m	coeficiente de arrastre
m	68.1 Kg	masa
L	30 m	Longitud de la cuerda
k	40 N/m	constante de resorte de la cuerda
γ	8 N s/m	coeficiente de amortiguamiento de la cuerda
signo(v)	función que devuelve –1, 0 y 1, para v negativa, cero y positiva, respectivamente

En conocimiento que la primera ecuación es válida solo hasta t_c=2.55, L=30mts, v= 23.20752.
Encuentre el tiempo t_d cuando se alcanza la longitud MÁXIMA de la cuerda extendida y estirada por completo, es decir y>L, con velocidad = 0. (solo 2da ecuación)

a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b. Desarrolle tres iteraciones para y(t) con tamaño de paso h=0.5

c. Usando el algoritmo, aproxime la solución para y en el intervalo entre [0,t_c], adjunte sus resultados.txt

d. Indique el valor de t_d, muestre cómo mejorar la precisión y realice sus observaciones sobre los resultados.

Observación: dy/dt = v, función signo(v) en Numpy:np.sign(v)

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c resultados.txt y grafica.png (10 puntos), literal d (5 puntos),

Referencia: [1] Chapra. capítulo 28. Ejercicio 28.41 p852.

[2] Extreme Bungy Jumping with Cliff Jump Shenanigans! Play On in New Zealand! 4K! – devinsupertramp. 23 mar 2015.

2024-02-152024-02-20

3Eva_2023PAOII_T3 Volumen por solido de revolución de un peón

3ra Evaluación 2023-2024 PAO II. 15/Febrero/2024

Tema 3 (40 puntos) Los sólidos de revolución se generan al girar una región plana alrededor de un eje.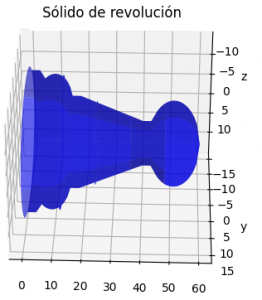

El volumen generado al girar la región de una función f(x) en el intervalo [a,b], se puede calcular como el volumen del disco de radio f(x) y anchura dx.

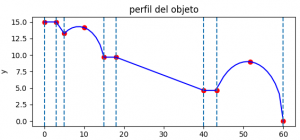
V = \int_{a}^{b} \pi (f(x))^2 dx

Calcule el volumen de revolución generado por la región sombreada y limitada los puntos de la tabla del tema anterior y la gráfica 2D mostrada.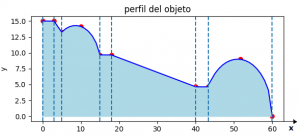

Realice el ejercicio usando para los integrales el método de integración por Cuadratura de Gauss para al menos lo tres primeros intervalos.

xi=[ 0, 3, 5.  , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60]
yi=[15,15,13.25,14.1552, 9.6768,  9.67,  4.64,  4.64,  8.9768, 0.]

Para el desarrollo de cada intervalo:
a. Realice el planteamiento de las formulas de volumen de sólido de revolución.
b. Desarrolle las expresiones completas con valores numéricos que permitan revisar sus operaciones.
c. Indique el resultado obtenido para cada integral.
d. Determine el volumen de revolución generado por la región sombreada presentada en la gráfica usando el algoritmo en Python.
e. Adjunte sus resultados.txt y algoritmos.py

Rúbrica: literal a (12 puntos), literal b (12 puntos), literal c (6 puntos), literal d (5 puntos), literal e (5 puntos)

Referencia: [1] Volúmenes de sólidos de revolución. Moisés Villena Muñoz. Capítulo 4 p78. https://www.dspace.espol.edu.ec/bitstream/123456789/4800/4/7417.pdf

[2]Curso Torno Madera. Práctica de realización de peón de ajedrez. Taller Escuela Pinocho. 21 octubre 2021

2024-02-152024-02-20

3Eva_2023PAOII_T2 perfil de un peón

3ra Evaluación 2023-2024 PAO II. 15/Febrero/2024

Tema 2 (30 puntos) Las medidas del perfil de un objeto se describen por medio de los siguientes puntos:

x_i	0	3	5	9.985	14.97	17.97	40.04	43.29	51.64560	60
y_i	15	15	13.25	14.155	9.676	9.676	4.64	4.64	8.976	0

a. Plantee el o los polinomios de interpolación P(x) que describan el perfil del objeto en el intervalo
[0, 14.97] . Justifique la selección del método de interpolación polinómica.

b. Desarrolle los polinomios planteados de forma analítica.

c. Estime el mayor error sobre el o los datos en el intervalo [5, 9.985]. Use como referencia la ecuación del círculo del tema anterior.

d. Escriba sus conclusiones y recomendaciones sobre los resultados obtenidos. Adjunte los archivos realizados como algoritmos.py, resultados.txt y gráficas.png

Rúbrica: literal a (9 puntos), literal b (12 puntos), literal c (6 puntos), literal d (3 puntos)

xi=[ 0, 3, 5.  , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60]
yi=[15,15,13.25,14.1552, 9.6768,  9.67,  4.64,  4.64,  8.9768, 0.]

2024-02-152024-10-08

3Eva_2023PAOII_T1 Intersección con círculo

3ra Evaluación 2023-2024 PAO II. 15/Febrero/2024

Tema 1 (30 puntos) Encuentre las raíces de las ecuaciones simultaneas siguientes:

2y+1.75 x= 35.25

(y-7.6)^2 + (x-8.6)^2 = (6.7)^2

a. Use el enfoque gráfico para obtener los valores iniciales. Presente la gráfica realizada con Python.
b. Encuentre un intervalo apropiado para aproximar este valor mediante el método de Newton-Raphson
c. Realice al menos 3 iteraciones de forma analítica, usando tolerancia de 10^-4
d. Realice el análisis de la convergencia del método.
Adjunte los archivos realizados como algoritmos.py, resultados.txt y gráficas.png

Rúbrica: literal a (5 puntos), literal b (5 puntos), iteraciones(9 puntos), errores entre iteraciones (6 puntos), análisis de convergencia (5 puntos).

2023-09-132023-09-15

3Eva_2023PAOI_T4 Especies en competencia por recursos

3ra Evaluación 2023-2024 PAO I. 12/Septiembre/2023

Tema 4. (30 puntos) Considere dos especies de animales que ocupan el mismo ecosistema, en competencia por los recursos de alimentos y espacio definidas por:

\frac{dx}{dt} = x(2 - 0.4 x - 0.3 y)

\frac{dy}{dt} = y( 1 - 0.1 y - 0.3 x)

Donde las poblaciones de x(t) y y(t) se miden en miles y t en años. Use un método numérico para analizar las poblaciones en un periodo largo para el caso que: x(0)=1.5, y(0)=3.5

a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b. Desarrolle tres iteraciones para x(t), y(t) con tamaño de paso h=0.5.

c. Usando el algoritmo, aproxime la solución entre t=0 a t=10 años, adjunte sus resultados en la evaluación.

d. Realice una observación sobre el crecimiento de la población de las especies y(t) a lo largo del tiempo.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d (5 puntos)

Referencia: [1] Modelos de competencia ejercicio 10. Zill, Dennis G. Ecuaciones diferenciales con aplicaciones de modelado. Edición 9. P109. p111.

[2] Competition in ecosystems. Stile Education. 11 septiembre 2019.

2023-09-132023-09-15

3Eva_2023PAOI_T3 Perfil de área devastada por incendios

3ra Evaluación 2023-2024 PAO I. 12/Septiembre/2023

3Eva_2023PAOI_T2 Área devastada por incendios

Tema 3. (20 puntos) Continuando con el ejercicio del área devastada por el incendio, con el objetivo de simplificar el registro de datos se propone describir los perfiles usando polinomios.

Frontera superior

X	350	300	350	420	444	484	504	534	568	620	660	720	780	740	800	800
Y	0	315	315	315	320	336	400	415	462	510	550	550	490	390	390	150

Frontera inferior

X	350	459	666	800
Y	0	63	130	150

a. Plantear el ejercicio para realizar interpolación polinómica. Describa criterios, intervalos, método.

b. Desarrolle el o los polinomios para la frontera superior, siguiendo el método propuesto en el literal a.

c. Desarrolle el o los polinomios para la frontera inferior, con un método diferente al literal a.

d. Usando un algoritmo, graficar al menos un resultado del literal b y c.

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (5 puntos)

2023-09-132024-01-18

3Eva_2023PAOI_T2 Área devastada por incendios

3ra Evaluación 2023-2024 PAO I. 12/Septiembre/2023

Tema 2 (25 puntos) Se requiere determinar el área urbana a restaurar, que devastada por incendios en una isla del océano Pacífico, se encuentra delimitada por la playa y los puntos mostrados en la figura.

Se dispone de algunos puntos de referencia tomados desde imágenes de satélites mostrados en la tabla.

a. Plantear el ejercicio indicando el método de integración numérica a usar. Justifique su selección.

b. Desarrolle el método para los datos de la frontera superior

c. Realice los cálculos para la frontera inferior delimitada por playa

d. Estime la cota de error en los cálculos.

Frontera superior

X	350	300	350	420	444	484	504	534	568	620	660	720	780	740	800	800
Y	0	315	315	315	320	336	400	415	462	510	550	550	490	390	390	150

Frontera inferior

X	350	459	666	800
Y	0	63	130	150

Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (5 puntos), literal d (5 puntos)

xs = [350, 300, 350, 420, 444, 484, 504, 534, 568, 620, 660, 720, 780, 740, 800, 800]
fs = [0, 315, 315, 315, 320, 336, 400, 415, 462, 510, 550, 550, 490, 390, 390, 150]
xi = [350, 459, 666, 800]
fi = [0, 63, 130, 150]

Referencia: Incendios forestales devastan partes de la isla de Maui. DW español. 11 agosto 2023.

2023-09-132023-09-15

3Eva_2023PAOI_T1 Matriz cadena de Markov

3ra Evaluación 2023-2024 PAO I. 12/Septiembre/2023

Tema 1 (25 puntos) Un call-center para soporte técnico de una mediana empresa se conforma de una recepcionista y dos técnicos. Se considera como “satisfecho” al cliente si su llamada fue procesada por la recepcionista y cualquiera de los técnicos.

La probabilidad P_RT de atención a llamadas se modelan con un sistema de ecuaciones (cadena de Markov) que al ser resuelta muestra probabilidad de encontrarse en cada estado.

λ P₀₀ = μ_T P₀₁

(μ_T + λ) P₀₁ = 2 μ_T P₀₂ + μ_R P₁₀

(2 μ_T + λ) P₀₂ = μ_R P₁₁ + μ_R P₁₂

μ_R P₁₀ = λ P₀₀ + μ_T P₁₁

(μ_R + μ_T) P₁₁ = λ P₀₁ + 2 μ_T P₁₂

(μ_R + 2 μ_T) P₁₂ = λ P₀₂

La suma de probabilidades es uno.

P₀₀ + P₀₁ + P₀₂ + P₁₀ + P₁₁+ P₁₂ = 1

λ = 1/10, μR = 1/3, μT =1/15

Los estados descritos en la gráfica y ecuaciones expresan el proceso de atención:
– En una llamada, los clientes son atendidos por la recepcionista que toma los datos y redirige la llamada a uno de los técnicos disponible (libre).
– Si un cliente llama mientras la recepcionista está ocupada, el cliente recibe tono de ocupado y cierra.
– Si ambos técnicos están disponibles, se selecciona uno con igual probabilidad.
– Si solo hay un técnico disponible, se le asigna la llamada.
– Si los dos técnicos están ocupados, se pierde la llamada.

Los tiempos de atención y llamadas siguen distribuciones exponenciales: recepcionista es de 3 minutos (μR = 1/3), por técnico es de 15 minutos (μT =1/15). Los clientes llaman a intervalos de 10 minutos (λ = 1/10).

a. Plantee el sistema de ecuaciones, reemplazando la última ecuación con la que indica que la suma de probabilidades por cada estado P_RT suma 1.

b. Establezca la forma matricial del sistema de ecuaciones y como matriz aumentada

c. De ser necesario realice el pivoteo parcial por filas.

d. Comente sobre la convergencia del sistema de ecuaciones y justifique sus observaciones usando los errores entre iteraciones o número de condición.

e. Use un método directo, realizando al menos 3 iteraciones con todas las expresiones.

Rúbrica: literal a (2 puntos), literal b (5 puntos), literal c (3puntos), literal d (5 puntos), literal e (10 puntos).

Referencia: [1] 1Eva_IT2017_T3 Call Center Operadora y Dos Técnicos. ESTG1003-Blog de procesos estocásticos. http://blog.espol.edu.ec/estg1003/1eva_it2017_t3-call-center-operadora-y-dos-tecnicos/
[2] Cadenas de Markov 01 Introducción. Goal Project. 30 agosto 2021.