Ejercicio: 1Eva_IIT2008_T1 Distribuidores de productos
literal a
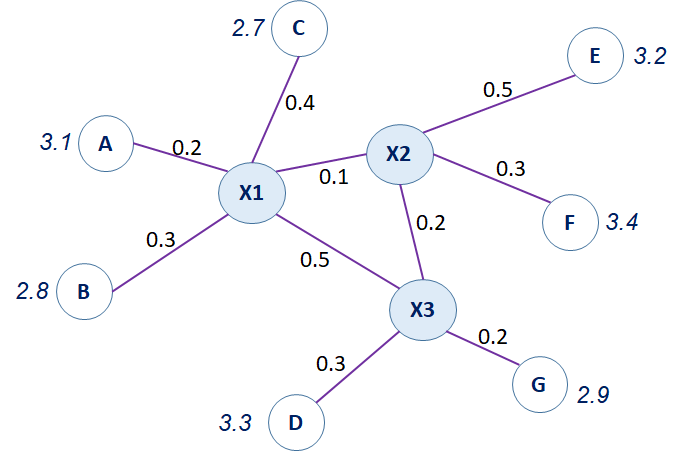
Siguiendo las instrucciones del enunciado, el promedio de precios del nodo A, se conforma de los precios en los nodos aledaños menos el costo de transporte.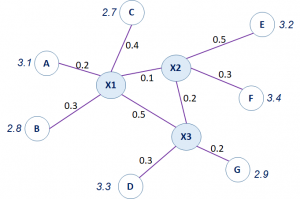
precio en X1 para A = precio en nodoA – costo de transporteA
siguiendo el mismo procedimiento,
precio en X1 para A: (3.1-0.2)
precio de X1 para B: (2.8-0.3)
precio de X1 para C: (2.7-0.4)
precio de X1 para X2: (X2-0.1)
precio de X1 para X3: (X3-0.5)
x_1 = \frac{1}{5} \Big[ (3.1-0.2)+(2.8-0.3)+(2.7-0.4)+
+(x_2-0.1)+(x_3-0.5)\Big]
x_1 = \frac{1}{5} \Big[ 2.9+2.5 +2.3+x_2+x_3-0.6\Big]
x_1 = \frac{1}{5} (7.1+x_2+x_3)
5x_1 = 7.1+x_2+x_3
5x_1-x_2-x_3 = 7.1
Se continua con el mismo proceso para los siguientes nodos:
x_2 = \frac{1}{4} \Big[ (3.2-0.5)+(3.4-0.3) +(x_1-0.1)+(x_3-0.2)\Big]
4x_2 = (3.2-0.5)+(3.4-0.3) +(x_1-0.1)+(x_3-0.2)
4x_2 = 2.7+3.1 +x_1+x_3-0.3
-x_1+4x_2-x_3 = 5.5
Para X3
x_3 = \frac{1}{4} \Big[ (3.3-0.3)+(2.9-0.2) +(x_1-0.5)+(x_2-0.2)\Big]
4x_3 = 3.0+2.7+x_1+x_2-0.7
4x_3 = 5+x_1+x_2
-x_1-x_2+4x_3= 5
El sistema de ecuaciones se convierte en:
\begin{cases} 5x_1-x_2-x_3 = 7.1 \\ -x_1+4x_2-x_3 = 5.5 \\-x_1-x_2+4x_3= 5 \end{cases}
Para resolver se cambia a la forma Ax=B
\begin{bmatrix} 5 && -1 && -1 \\ -1 && 4 && -1 \\ -1 && -1 && 4 \end{bmatrix} . \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 7.1 \\ 5.5 \\5 \end{bmatrix}
En los métodos directos se usa la forma de matriz aumentada
\begin{bmatrix} 5 && -1 && -1 && 7.1 \\ -1 && 4 && -1 && 5.5 \\ -1 && -1 && 4 && 5 \end{bmatrix}
pivoteo: no es necesario, pues la matriz ya está ordenada de forma diagonalmente dominante.
Eliminación hacia adelante
i=0, f=0
\begin{bmatrix} 5 && -1 && -1 && 7.1 \\ -1-5\big(\frac{-1}{5}\big) && 4 -(-1)\big(\frac{-1}{5}\big) && -1 -(-1)\big(\frac{-1}{5}\big) && 5.5-7.1\big(\frac{-1}{5}\big) \\ -1-5\big(\frac{-1}{5}\big) && -1-(-1)1\big(\frac{-1}{5}\big) && 4-(-1)\big(\frac{-1}{5}\big) && 5-7.1\big(\frac{-1}{5}\big) \end{bmatrix}
\begin{bmatrix} 5 && -1 && -1 && 7.1 \\ 0 && 3.8 && -1.2 && 6.92 \\ 0 && -1.2 && 3.8 && 6.42 \end{bmatrix}
Eliminación hacia adelante para i = 1, j=1
Elimina hacia adelante
[[ 5. -1. -1. 7.1 ]
[ 0. 3.8 -1.2 6.92 ]
[ 0. 0. 3.42105263 8.60526316]]
Eliminación hacia atrás, continuando el desarrollo de forma semejante a los pasos anteriores se obtiene:
Elimina hacia atrás
[[ 1. -0. -0. 2.44615385]
[ 0. 1. -0. 2.61538462]
[ 0. 0. 1. 2.51538462]]
el vector solución X es:
[[2.44615385]
[2.61538462]
[2.51538462]]
verificar que A.X = B
[[7.1]
[5.5]
[5. ]]
literal b
Para el literal b se usa como referencia el número de condición:
>>> np.linalg.cond(A)
2.5274158815808474
El número de condición es cercano a 1, dado que la matriz A es diagonalmente dominante pues los valores mayores de la fila se encuentran en la diagonal. Como el número de condición es cercano a 1 el sistema converge usando métodos iterativos.
La selección del vector inicial para las iteraciones siguiendo el enunciado del problema, se evita el vector cero dado que el precio de un producto para una fabrica no puede ser cero. Se observa los valores de los precios, y se encuentra que el rango de existencia en los nodos es [ 2.7, 3.4] que restando el valor de transporte podrían ser un valor menor a 2.7. Por lo que un buen vector inicial será [2,2,2]
literal c
Se plantean las ecuaciones para el método de Jacobi a partir del sistema de ecuaciones, a partir del pivoteo por filas:
\begin{cases} 5x_1-x_2-x_3 = 7.1 \\ -x_1+4x_2-x_3 = 5.5 \\-x_1-x_2+4x_3= 5 \end{cases}
x_1 = \frac{7.1 +x_2 + x_3}{5}
x_2 = \frac{ 5.5 +x_1 + x_3}{4}
x_3 = \frac{5 +x_1 + x_2}{4}
Si consideramos que el costo mínimo podría ser 2, el precio debería ser mayor x0 = [2,2,2]
itera = 0
x_1 = \frac{7.1 +(2) + (2)}{5} = 2.22
x_2 = \frac{ 5.5 +(2) + (2)}{4} = 2.375
x_3 = \frac{5 +(2) + (2)}{4} =2.25
errado = max|[2.22-2, 2.375-2, 2.25-2]|
= max |[0.22, 0.375, 0.25]| = 0.375
X_1 = [2.22, 2.375, 2.25]|
itera = 1
x_1 = \frac{7.1 +(2.375) + (2.25)}{5} = 2.345
x_2 = \frac{ 5.5 +(2.22) + (2.25)}{4} = 2.4925
x_3 = \frac{5 +(2.22) + (2.375)}{4} =2.39875
errado = max|[2.345-2.22, 2.4925-2.375, 2.39875 - 2.25]|
= 0.14874999999999972
X_2 = [2.345, 2.4925, 2.39875]
itera = 2
x_1 = \frac{7.1 +(2.4925) + (2.39875)}{5} = 2.39825
x_2 = \frac{ 5.5 +(2.345) + (2.39875)}{4} = 2.5609375
x_3 = \frac{5 +(2.345) + (2.4925)}{4} = 2.459375
errado = max|[2.39825 - 2.345, 2.5609375- 2.4925, 2.459375 - 2.39875]|
= 0.06843749999999993
X_3 = [2.39825, 2.5609375, 2.459375 ]
El error disminuye entre iteraciones, por lo que el método converge.
Los datos de las iteraciones usando el algoritmo son:
Matriz aumentada
[[ 5. -1. -1. 7.1]
[-1. 4. -1. 5.5]
[-1. -1. 4. 5. ]]
Pivoteo parcial:
Pivoteo por filas NO requerido
itera,[X],errado
0 [2. 2. 2.] 1.0
1 [2.22 2.375 2.25 ] 0.375
2 [2.345 2.4925 2.39875] 0.14874999999999972
3 [2.39825 2.5609375 2.459375 ] 0.06843749999999993
4 [2.4240625 2.58940625 2.48979687] 0.030421875000000043
5 [2.43584062 2.60346484 2.50336719] 0.014058593750000181
6 [2.44136641 2.60980195 2.50982637] 0.006459179687499983
7 [2.44392566 2.61279819 2.51279209] 0.0029962402343750583
8 [2.44511806 2.61417944 2.51418096] 0.001388874511718985
9 [2.44567208 2.61482476 2.51482437] 0.0006453167724607134
10 [2.44592983 2.61512411 2.51512421] 0.00029983517456066977
11 [2.44604966 2.61526351 2.51526348] 0.0001393951034542873
12 [2.4461054 2.61532829 2.51532829] 6.480845146183967e-05
numero de condición: 2.5274158815808474
respuesta con Jacobi
[2.4461054 2.61532829 2.51532829]
Algoritmo en Python
# 1Eva_IIT2008_T1 Distribuidores de productos
# Método de Jacobi
import numpy as np
def jacobi(A,B,tolera,X0,iteramax=100, vertabla=False):
''' Método de Jacobi, tolerancia, vector inicial X0
para mostrar iteraciones: vertabla=True
'''
A = np.array(A, dtype=float)
B = np.array(B, dtype=float)
X0 = np.array(X0, dtype=float)
tamano = np.shape(A)
n = tamano[0]
m = tamano[1]
diferencia = np.ones(n, dtype=float)
errado = np.max(diferencia)
X = np.copy(X0)
xnuevo = np.copy(X0)
itera = 0
if vertabla==True:
print('itera,[X],errado')
print(itera, xnuevo, errado)
while not(errado<=tolera or itera>iteramax):
for i in range(0,n,1):
nuevo = B[i]
for j in range(0,m,1):
if (i!=j): # excepto diagonal de A
nuevo = nuevo-A[i,j]*X[j]
nuevo = nuevo/A[i,i]
xnuevo[i] = nuevo
diferencia = np.abs(xnuevo-X)
errado = np.max(diferencia)
X = np.copy(xnuevo)
itera = itera + 1
if vertabla==True:
print(itera, xnuevo, errado)
# No converge
if (itera>iteramax):
X=itera
print('iteramax superado, No converge')
return(X)
def pivoteafila(A,B,vertabla=False):
'''
Pivotea parcial por filas, entrega matriz aumentada AB
Si hay ceros en diagonal es matriz singular,
Tarea: Revisar si diagonal tiene ceros
'''
A = np.array(A,dtype=float)
B = np.array(B,dtype=float)
# Matriz aumentada
nB = len(np.shape(B))
if nB == 1:
B = np.transpose([B])
AB = np.concatenate((A,B),axis=1)
if vertabla==True:
print('Matriz aumentada')
print(AB)
print('Pivoteo parcial:')
# Pivoteo por filas AB
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
# Para cada fila en AB
pivoteado = 0
for i in range(0,n-1,1):
# columna desde diagonal i en adelante
columna = np.abs(AB[i:,i])
dondemax = np.argmax(columna)
# dondemax no es en diagonal
if (dondemax != 0):
# intercambia filas
temporal = np.copy(AB[i,:])
AB[i,:] = AB[dondemax+i,:]
AB[dondemax+i,:] = temporal
pivoteado = pivoteado + 1
if vertabla==True:
print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax)
if vertabla==True:
if pivoteado==0:
print(' Pivoteo por filas NO requerido')
else:
print('AB')
return(AB)
# INGRESO
A = [[ 5, -1, -1],
[ -1, 4, -1],
[ -1, -1, 4]]
B = [7.1, 5.5,5]
X0 = [2,2,2]
tolera = 0.0001
iteramax = 100
# PROCEDIMIENTO
# numero de condicion
ncond = np.linalg.cond(A)
# Pivoteo parcial por filas
AB = pivoteafila(A,B,vertabla=True)
n = len(A)
A = AB[:,:n]
B = AB[:,n]
respuesta = jacobi(A,B,tolera,X0,vertabla=True)
# SALIDA
print('numero de condición:', ncond)
print('respuesta con Jacobi')
print(respuesta)