2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 4. (20 puntos) Utilizando el polinomio de grado 2, deduzca el método de Simpson 1/3.
2Eva_IT2015_T3 EDP parabólica
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 3. (30 puntos) Use el método de diferencias progresivas para aproximar la solución de la ecuación diferencial parcial parabólica
\frac{\partial u}{\partial t} - \frac{4}{\pi ^2}\frac{\partial ^2 u}{\partial x^2} = 0 0 \lt\ x \lt 4, 0\lt t u(0,t) = u(4,t) = 0, 0\lt t u(x,0) = \sin \Big( \frac{\pi}{4}x \Big) \Big( 1 + 2 \cos \Big( \frac{\pi}{4}x\Big)\Big) 0 \leq x \leq 4a) Use n=20 en el sentido de x; y m=10, obtenga el modelo (solo planteado).
b) Aproxime la solución con n=4, hasta 2Δt, y
c) estime el error en el punto P(x1, t1)
2Eva_IT2015_T1 Fibra óptica entre montañas
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 1. (20 puntos) Para una fibra óptica que para por montañas se tienen las medidas de distancia vertical en función de la distancia horizontal y se muestra en la figura y la tabla.
| horizontal x | vertical y |
| 0 | 0 |
| 100 | 25 |
| 200 | 38 |
| 300 | 45 |
| 400 | 20 |
a. Encuentre y’ en los puntos de la tabla usando una aproximación de O(h2)
b. Usando La regla de Simpson 1/3 aproxime la longitud del cable y estime el error.
x = [ 0, 100, 200, 300, 400] y = [ 0, 25, 38, 45, 20]
2Eva_IT2015_T2 Deflexión de mástil
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 2. (30 puntos) La ecuación siguiente se utiliza para modelar la deflexión del mástil de un bote expuesto a la fuerza del viento:
\frac{\delta ^2 y}{\delta x^2} = \frac{f}{2EI} (L-x)^2Donde:
f = fuerza,
E = módulo de elasticidad,
L = longitud del mástil
I = momento de inercia.
Calcule la deflexión si y = 0 y \frac{\delta y}{\delta x} = 0 en x = 0.
Para sus cálculos considere f=60, L =30, E = 1.25×108 e I = 0.05.
a. Encuentre el sistema de ecuaciones diferenciales equivalente a dicha ecuación.
b. Aproxime usando Runge-Kutta 4to orden, para n=30 sub-intervalos. (solo expresado)
c. Aproxime considerando h=2 y realice 2 pasos usando Runge-Kutta de 2do orden.
Referencias: Chapra 24.2 p284 pdf121
2Eva_IIT2014_T3 EDP Hiperbólica, Presión en tubo musical
2da Evaluación II Término 2014-2015. 23/Febrero/2015. ICM00158
Tema 3. En un tubo de órgano musical, la presión del aire p(x,t) se rige por la ecuación de onda 
Donde L es la longitud del tubo y c es una constante física.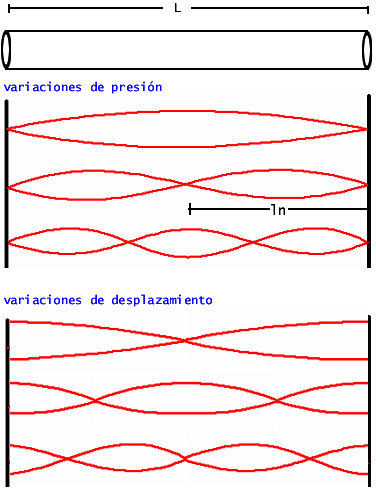
Si el tubo se encuentra abierto, las condiciones de frontera estarán dadas por:
p(0,t) = p0
p(L,t) = p0
Si el tubo está cerrado en el extremo donde x=L, las condiciones de frontera serán:
p(0,t) = p0
\frac{\partial p(l,t)}{\partial x} = 0
Suponga que c=1, L=1 y que las condiciones iniciales son
p(x,0) = p0 cos(2πx)
\frac{\partial p(x,0)}{\partial t} = 0
0 \leq x \leq L
a. Aproxime la presión de un tubo abierto usando las diferencias finitas con p0 = 0.9 en x = 1/2 para t = 0.5 y t = 1,
b. Modifique el procedimiento del literal a para el problema del tubo de órgano cerrado con p0 = 0.9 y luego aproxime p(0.5 , 0.5) y p(0.5 , 1) usando h = 0.1 y k = 0.1
2Eva_IIT2014_T2 Carga uniforme en viga
2da Evaluación II Término 2014-2015. 23/Febrero/2015. ICM00158
Tema 2. La ecuación diferencial básica de la curva elástica para una viga con carga uniforme (ver figura) está dada por
EI \frac{\delta ^2 y}{\delta x^2} = \frac{wLx}{2} - \frac{wx^2}{2}
Donde E = módulo de elasticidad, I = momento de inercia
Resuelva para la deflexión de la viga con el método de disparo con Runge-Kutta de 2do orden y (Δx = 2.5 ft).
Aplique los siguientes valores de parámetros:
E = 30.000 ksi
I = 800 in4
w = 1 kip/in
L = 10 ft.
Referencia: Chapra 5Ed Cap28 Ejercicio 28.23 p849 pdf873.
2Eva_IIT2014_T1 Coeficiente Gini
2da Evaluación II Término 2014-2015. 23/Febrero/2015. ICM00158
Tema 1. El coeficiente de Gini(1) se calcula como una proporción de las áreas en el diagrama de la curva de Lorenz. 
Si el área entre la línea de perfecta igualdad y la curva de Lorenz es a, y el área por debajo de la curva de Lorenz es b, entonces el coeficiente de Gini es a/(a+b).
X: Proporción acumulada de la Población,
Y: Proporción acumulada de los Ingresos
Los siguientes datos corresponden a los ingresos, anuales ordenados, de 10 personas representativas en una sociedad:
ingresos = [2500, 4500, 6000, 8000, 14000, 25000, 30000, 45000, 60000, 90000]
acumule los datos de menor a mayor y estime el coeficiente de Gini para dicha sociedad utilizando la técnica de integración de Simpson 1/3 y aproxime la cota del error.
Referencia: (1) «Gini coefficient». Publicado bajo la licencia CC BY-SA 3.0 vía Wikimedia Commons – http: //commons.wikimedia.org/wiki/File:Gini_coefficient.svg#mediaviewer/File:Gini_coefficient.svg.
En documental, El coeficiente Gini, a partir del minuto 5:00, durante al menos 8:12
País de desigualdad (1/3) | DW Documental