Publicado en

1Eva_IIT2008_T2 Sortear jueces para salas CNJ

1ra Evaluación II Término 2008 – 2009. Diciembre 09, 2008 /ICM00794

Tema 2 (25 puntos). En el proceso de transición institucional que establece la nueva Constitución, aprobada en el referendo del pasado 28 de septiembre del 2008, la principal entidad jurisdiccional será la Corte Nacional de Justicia (CNJ). (www.eluniverso.com 25/octubre/2008)

La CNJ estará conformada por 21 de 31 jueces que integraron la anterior Corte Suprema de Justicia (CSJ) y escogidos mediante sorteo público.

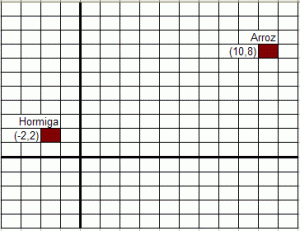
Realice un algoritmo que permita realizar el sorteo público de n entre m jueces de la CSJ (15 puntos) y los muestre en forma ordenada (10 puntos).

Nota.- Cada juez se representa por un número, en el sorteo no deben repetirse los jueces escogidos

Publicado en

1Eva_IT2008_T2 Criba de Eratóstenes con Python

1ra Evaluación I Término 2008 – 2009. Julio 08, 2008 /ICM00794

Tema 2 (20 puntos). Una forma de hallar todos los números primos menores que un número natural n, es el método de la “Criba de Eratóstenes” que consiste en lo siguiente:

Ejemplo: Para n=20

  • Se forma un vector con todos los números
    naturales entre 2 y n.
  • Se tachan todos los múltiplos de 2
    que son menores que n,
  • luego se tachan los múltiplos de 3
    que son menores que n,
    y así sucesivamente.
  • El procedimiento se repite hasta alcanzar
    todos los múltiplos de los números naturales
    menores que n.
  • Los números no tachados
    corresponden a los números primos.

Primos: 2, 3, 5, 7, 11, 13, 17, 19

Elabore un algoritmo que, dado un número
entero positivo n mayor que 1,
muestre los números primos
encontrados con el método descrito.

 i criba[i]
2 1
3 1
4 0
5 1
6 0
7 1
8 0
9 0
10 0
11 1
12 0
13 1
14 0
15 0
16 0
17 1
18 0
19 1
20 0

 

Publicado en

1Eva_IT2008_T1 Teorema de Wilson

1ra Evaluación I Término 2008 – 2009. Julio 08, 2008 /ICM00794

Tema 1 (20 puntos). El teorema de Wilson enuncia que:

“Un número p es primo si y solo si el factorial (p-1)! + 1 es divisible por p”.

Escriba un algoritmo que solicite al usuario un número entero positivo p, determine si es primo, en el caso de serlo verifique que se cumple el teorema de Wilson.

Publicado en

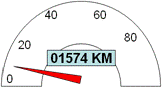1Eva_IIT2008_T1 Odómetro OCTAL

1ra Evaluación II Término 2008 – 2009. Diciembre 09, 2008 /ICM00794

Tema 1 (20 puntos). En un odómetro mecánico de un vehículo antiguo se marcan las distancias recorridas en kilómetros, en formato numérico octal de hasta cinco dígitos.

odometroRealice un algoritmo para encontrar la distancia recorrida en kilómetros en formato numérico decimal, convirtiendo el valor octal marcado por el odómetro luego de un viaje.

Nota: Un odómetro es un dispositivo que indica la distancia recorrida en un viaje de un vehículo.

Publicado en

1Eva_IT2007_T3 Elección de diputados provinciales

1ra Evaluación I Término 2007 – 2008. Julio 03, 2007 /ICM00794

Tema 3 (40 puntos) En un proceso electoral para elegir a diputados provinciales, la asignación del número de diputados para cada partido electoral se lo hace en forma proporcional, de acuerdo a la votación obtenida por el partido y el total de votos en cada provincia. votacion

a) (20 puntos) Escriba un algoritmo que solicite al usuario para m provincias:

  • el total de registrados en padrón para esa provincia (habilitados para votar),
  • la cantidad de diputados a elegir en esa provincia,
  • la cantidad de votos obtenidos por la lista ABC,
    los cuales deben ser almacenados en los vectores padrón, elegir y votos respectivamente.

Su algoritmo debe calcular, para cada provincia, la cantidad de diputados que alcanzó el partido ABC, y almacenar dicha información en un nuevo vector diputados.

b) (20 puntos) Adicionalmente determine, el promedio de diputados que alcanzo el partido ABC, y en qué provincia obtuvo la mayor representación, de acuerdo al número de diputados.

provincia padrón elegir votos diputados
1 970 12 658 8
2 1500 9 430 …
3 760 4 320 …
… … … … …
m 
Ejemplo:
El Partido ABC ha participado con su lista de candidatos y en una provincia de un total en el padrón de 970, obtuvo 658 votos; 
por lo que de 12 a elegir el partido obtuvo 8 diputados.
 La cantidad de diputados se calculó así:
 (658/970)*12 = 8.14, usando redondeo simple.
Publicado en

1Eva_IIT2007_T3 Garantías de prestamos IESS

1ra Evaluación II Término 2007 – 2008. Diciembre 04, 2007 /ICM00794

Tema 3 (40 puntos) El instituto Ecuatoriano de Seguridad Social (IESS) ofrece un préstamo a los afiliados, el que es garantizado con los valores depositados en “fondos de reserva” y “cesantías”.

Con el objetivo de conocer el número de afiliados que están en capacidad de realizar los préstamos, se solicitó un listado de número de cédula de afiliados al departamento “fondos de reserva” y otro al departamento “cesantía” debido a que operan todavía de manera independiente.

Realice un algoritmo que muestre la cantidad de afiliados que cumplen con las condiciones para el préstamo (se encuentran en los dos listados) y luego muestre los números de cédula encontrados.

Nota: Existen n afiliados con “fondos de reserva” y m afiliados con valores de “cesantía”.

Para el ejemplo mostrado se usan números solo de 3 dígitos, solo para la explicación

i reserva(i)
1 987
2 876
3 765
4 654
… …
n
j cesantia(j)
1 876
2 765
3
..
m

Referencia: BIESS otorgará préstamos hipotecarios con tasas de interés desde 5,99%. agosto 20, 2019. http://www.teleamazonas.com/2019/08/biess-otorgara-prestamos-hipotecarios-con-tasas-de-interes-desde-599/

Publicado en

1Eva_IIT2007_T2 Juego de la Ruleta

1ra Evaluación II Término 2007 – 2008. Diciembre 04, 2007 /ICM00794

Tema 2. (30 puntos) En los casinos, el “juego de la ruleta”

ruletacasino

consiste en acertar cuál será el número en donde caerá la bola que lanza el crupier en un círculo numerado del 1 al 36, con colores rojo y negro.

3 6 9 12 15 18 21 24 27 30 33 36
2 5 8 11 14 17 20 23 26 29 32 35
1 4 7 10 13 16 19 22 25 28 31 34

Escriba un algoritmo que simule este juego de azar para n jugadores que tienen la posibilidad de jugar durante m intentos cada uno.

Al final, indique cuál fue el número de la ruleta que salió la menor cantidad de veces (suponga que fue uno solo), para cada jugador.

Nota: para cada intento, cada jugador apuesta a un solo número, las apuestas a un número no se repiten.

Publicado en

1Eva_IIT2007_T1 Hormiga busca arroz

1ra Evaluación II Término 2007 – 2008. Diciembre 04, 2007 /ICM00794

Tema 1. (30 puntos)

En un plano cartesiano se encuentran una hormiga y un grano de arroz.

En cada instante de tiempo, la hormiga de manera aleatoria intuye la dirección donde ir (arriba, abajo, derecha, izquierda), y cuantas unidades desplazarse (entre 1 a 3) en la anterior dirección.

HormigaArrozImplemente un algoritmo que simule 100 instantes de tiempo con desplazamientos de la hormiga que inicialmente se encuentra en las coordenadas (-2,2) y un grano de arroz en las coordenadas (10,8).

Al final indique las respuestas a las siguientes preguntas:

a) ¿La hormiga llegó al grano de arroz?

b) Si la respuesta a la pregunta anterior es “Si”, entonces mostrar: cuántos pasos fueron necesarios.

c) ¿La distancia más lejana en la que estuvo la hormiga del grano de arroz?

Nota: La distancia entre dos puntos en el plano P1(x1, y1) y P2(x2, y2), viene dada por la siguiente expresión matemática:

d(P_1,P_2) = \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2 }
Publicado en

1Eva_IIT2006_T4 Vehículo de carga 3 con espacios

1ra Evaluación II Término 2006 – 2007. Diciembre 05, 2006 /ICM00794

Tema 4. (30 puntos) Se dispone de un vehículo con una capacidad de transportación de max Kilogramos y espacio para ubicar solo 3 paquetes del mismo tamaño pero de diferente peso.

camion carga en tres segmentos

Se tiene una lista con los pesos de n paquetes (también en kilogramos) de igual tamaño.

Si se desea transportar los paquetes agrupándolos de 3 en 3, indique:

  • ¿Cuántas combinaciones de las posibles ternas se pueden transportar a la vez?
  • Elabore un algoritmo que solicite al usuario los valores de max, la cantidad de paquetes n, los Pesos individuales y muestre la información solicitada.
Ejemplo: capacidad max=10 Kg y n paquetes
    i = [ 1, 2, 3, 4, 5, 6, ...,  n ]
Pesos = [ 5, 4, 3, 2, 5, 1, ..., ...]

Total de Ternas:
Suma Peso= 5+4+3;    0
Suma Peso= 5+4+2;    0
Suma Peso= 5+4+5;    0
Suma Peso= 5+4+1;    1
...
Suma Peso= 5+3+2;    2
Suma Peso= 5+3+5;    0
Suma Peso= 5+3+1;    3
...
Publicado en

1Eva_IIT2006_T3 Conejo en tablero

1ra Evaluación II Término 2006 – 2007 /ICM00794

Tema 3. (30 puntos) Suponga que un conejo se encuentra ubicado en el centro de un tablero cercado de 10×10 y con una salida en el lugar que se muestra en la figura. conejo perfil sombra

Si cada vez que el conejo salta 1 casilla, se conoce que lo puede realizar de forma aleatoria hacia arriba, abajo, izquierda o derecha.

Elabore un algoritmo que determine cuántos intentos debe realizar el conejo hasta que sale del tablero.

10 salida
9
8
7
6
5 Inicio
4
3
2
1 … … … … … … … … … …
1 2 3 4 5 6 7 8 9 10