Ejercicios sugeridos para desarrollar con listas, siguiendo los conceptos de ésta unidad.
1Eva_IIT2013_T4 Sorteo series mundial de fútbol
1Eva_IIT2011_T4 Impuestos casillas/envíos del exterior
4.4.1 Listas – Ejemplos con Python
Ejercicios resueltos de programación usando listas en Python
Operaciones de selección de datos desde listas
3Eva_IIIT2003_T2 Socios del club por género
Solución propuesta: s3Eva_IIIT2003_T2 Socios del club por género
Unión e Intersección de listas
3Eva_IT2002_T3 Determinar productos iguales entre vendedores
Solución propuesta: s3Eva_IT2002_T3 Determinar productos iguales entre vendedores
1Eva_IIT2007_T3 Garantías de prestamos IESS
Solución propuesta: s1Eva_IIT2007_T3 Garantías de prestamos IESS
1Eva_IIT2012_T4 Informe de pasantías
Solución propuesta: s1Eva_IIT2012_T4 Informe de pasantías
1Eva_IIT2010_T1 Censo de instrucción por género
Solución propuesta: s1Eva_IIT2010_T1 Censo de instrucción por género
1Eva_IT2010_T1 Bono para televisores en Uruguay
Solución propuesta: s1Eva_IT2010_T1 Bono para televisores en Uruguay
Arreglos y Aleatorios, random, numpy
3Eva_IT2005_T4 Tabla de Pozo millonario
Solución propuesta: s3Eva_IT2005_T4 Tabla de Pozo millonario
1Eva_IIT2005_T3 Entrenamiento atleta: promedios
Solución propuesta: s1Eva_IIT2005_T3 Entrenamiento atleta: promedios
4.4 Listas como conjuntos en Python
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
Para el manejo combinado de palabras y números, varias palabras, varias frases, se usa el concepto de Listas.
Las listas operan como un conjunto de datos de diferente tipo: cadenas junto a texto, conteniendo subconjunto de listas con diferentes dimensiones.
Una «lista» de datos como un vector es, por ejemplo, la lista del curso con los nombres de los participantes:
>>> lista = ['Juan','María','Pedro'] >>> lista ['Juan', 'María', 'Pedro'] >>> len(lista) 3 >>>
Añadir elementos: Append()
Luego ‘Ana’ decide registrarse en el curso, y debe añadirse su nombre a la lista del curso. La instrucción para añadir elementos en la lista es append() que es semejante a la instrucción de concatenar elemantos a un vector o una cadena.
>>> registrar = 'Ana' >>> listacurso.append(registrar) >>> listacurso ['Juan', 'María', 'Pedro', 'Ana'] >>>
Revisar Elemento en Conjunto
Siguiendo con el ejemplo anterior, para revisar si ‘Pedro’ y ‘Carlos’ se encuentra en la lista del curso. Si está en la lista, para identificar la posición o índice donde se encuentra, se usa la instruccion .index().
>>> 'Pedro' in listacurso
True
>>> 'Carlos' in listacurso
False
>>> donde = listacurso.index('Pedro')
>>> donde
2
Video Tutorial
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
Listas desde cadenas
Una frase se puede dividir en palabras, en referencia a un solo caracter:
>>> frase = 'El saber no ocupa lugar' >>> palabras = frase.split() >>> palabras ['El', 'saber', 'no', 'ocupa', 'lugar'] >>>
Listas de Listas
Las listas pueden agrupar otras listas, las notas individuales de cada estudiante se escribirían:
>>> califica = [['Juan',9],['María',10],['Pedro',6],['Ana',8]] >>> califica [['Juan', 9], ['María', 10], ['Pedro', 6], ['Ana', 8]] >>> califica[2] ['Pedro', 6] >>> califica[2][0] 'Pedro' >>> califica[2][1] 6 >>>
Note que en listas cuando se usa más de un índice, se usan corchetes independientes para cada índice.
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
4.3.2 Cadenas de caracteres/strings – Ejercicios
Ejercicios de programación propuestos para el uso de cadenas de caracteres/strings
2Eva_IT2012_T2 Número de tecla en cifrado musical con Python
2Eva_IT2010_T2 Operaciones infix – postfix
2Eva_IT2009_T1 Desordenar una palabra
2Eva_IIT2007_T1 Palabras aleatorias alternando vocal y consonante, genword
2Eva_IT2006_T3 Encriptar a Morse
3Eva_IIT2013_T3 buscar cadena en una frase
3Eva_IT2013_T1 Verificar un Abecegrama
3Eva_IIT2012_T1 Alfabeto radiofónico
4.3.1 Cadenas de caracteres/strings – Ejercicios resueltos en Python
Ejercicios resueltos de cadenas de caracteres o strings en programación con Python.
Solución Propuesta: s2Eva_IIT2012_T2 Cifrado César
video tutorial: S06T2E1 Cadenas de Caracteres. Cifrado César
2Eva_IT2005_T3 Adivina palabra (ahorcado)
Solución propuesta: s2Eva_IT2005_T3 Adivina palabra (ahorcado)
video tutorial: S06T2E2 Cadenas de Caracteres. Adivina palabra, ahorcado
2Eva_IIT2008_T2 Etiquetar a robots (R2D2)
Solución propuesta: s2Eva_IIT2008_T2 Etiquetar a robots (R2D2)
2Eva_IT2005_T1 Completar cadena con padright
Solución propuesta: s2Eva_IT2005_T1 Completar cadena con padright
2Eva_IT2011_T4 Números Romanos a decimal
Solución propuesta: s2Eva_IT2011_T4 Números Romanos a decimal
4.3 Cadenas de caracteres/strings – vector de letras en Python
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
El manejo de texto en computador requiere una representación de los símbolos o letras que se usan en un idioma.
Cada símbolo, letra o «caracter» que se presenta al escribir en pantalla se convierte en una sucesión ordenada de imágenes, semejante a agrupar las fichas del juego Scrabble
Una palabra se puede observar como las casillas de un vector, dando la pauta para el manejo de texto en el computador.
En Python, el texto para los mensajes en las preguntas input y las salidas print se escriben entre comillas " o apóstrofes '. Cada letra de una palabra se puede identificar por su posición como en un vector.
>>> palabra = 'manzana' >>> len(palabra) 7 >>> palabra[0] 'm' >>> palabra[4] 'a' >>>
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
Concatenar cadenas o strings
Si al unir palabras se forma una oración, el concepto se extiende a programación como «concatenar«. Básicamente concatenar es la unión de varias palabras para formar una oración un título o un mensaje.
>>> palabra1 = 'El' >>> palabra2 = 'saber' >>> frase = palabra1 + palabra2 >>> frase 'Elsaber' >>> frase = palabra1 + ' ' + palabra2 >>> frase 'El saber' >>> cadena1 = 'no ocupa lugar' >>> frase = frase + ' ' + cadena1 >>> frase 'El saber no ocupa lugar' >>>
Mayúsculas y Minúsculas con caracteres de letras
Para convertir una frase o palabra a mayúsculas o viceversa, se usan las instrucciones: palabra.upper() y palabra.lower().
Siguiendo el ejemplo anterior, el ejemplo de uso es:
>>> frase 'El saber no ocupa lugar' >>> enmayusculas = frase.upper() >>> enmayusculas 'EL SABER NO OCUPA LUGAR' >>> enminusculas = frase.lower() >>> enminusculas 'el saber no ocupa lugar' >>>
Comparar cadenas o strings
También es posible comparar caracteres, o cadenas entre si, por ejemplo para buscar cuántas vocales tiene una palabra. Considere que los caracteres o ‘dibujos de letras’ mayúsculas son diferentes a los de minúsculas.
>>> letra1 = 'd' >>> letra1 > 'a' True >>> letra1 > 'g' False >>> letra1 == 'D' False >>>
Se puede comparar el orden alfabético de los caracteres, pues el computador los almacena en una posición ordenada, semejante a un vector [‘a’,’b’,’c’, … ]
ejemplo con cadenas, o palabras:
>>> fruta1 = 'manzana' >>> fruta2 = 'pera' >>> fruta3 = 'manzana' >>> fruta4 = 'MANZANA' >>> fruta1 == fruta3 True >>> fruta1 == fruta2 False >>> fruta1 == fruta4 False >>>
Segmentar o dividir una cadena/string/texto usando split()
Para segmentar o dividir el texto por algún símbolo se dispone de la instrucción frase.split().
En el ejemplo se muestra como se separa la frase
>>> separa = frase.split() >>> separa ['El', 'saber', 'no', 'ocupa', 'lugar'] >>> separa[1] 'saber' >>>
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
4.2.2 Matrices en programación, Arreglos – Archivo Abrir/Guardar con Numpy
En Python se pueden obtener los datos de las matrices desde archivos, o almacenar las matrices hacia archivos. Así, cuando las matrices son de grandes dimensiones, no será necesario tener que escribir los valores de las matrices cada vez que se requiera hacer una operación.
En librería Numpy , existen funciones incorporadas para guardar o abrir una matriz desde un archivo en formato .txtcon las instrucciones: np.savetxt(), np.loadtxt()
Guardar matriz en archivo.txt con Numpy
Para guardar una matriz a un archivo use:
numpy.savetxt('matriz.txt', matriz)
>>> import numpy as np >>> matriz = np.array([[1,2,3],[4,5,6]]) >>> matriz array([[1, 2, 3], [4, 5, 6]]) >>> np.savetxt('matriz00.txt',matriz)
se puede encontrar en archivo.txt en el directorio de trabajo de Python
El archivo puede ser abierto para observar desde el «block de notas»
Abrir archivo.txt de una matriz con Numpy
Continuando con el ejercicio anterior, para abrir o leer desde un archivo en formato de texto ‘matriz.txt‘, se dispone de la instrucción de Numpy:
np.loadtxt('matriz.txt',dtype=int)
La instrucción permite indicar el tipo de datos que se usan en el arreglo.
>>> A = np.loadtxt('matriz00.txt',dtype=int)
>>> A
array([[1, 2, 3],
[4, 5, 6]])
>>> B = np.loadtxt('matriz00.txt')
>>> B
array([[ 1., 2., 3.],
[ 4., 5., 6.]])
Nota: lo importante es el formato del archivo en tipo texto. Algunas veces los archivos tienen extensión .dat que también pueden ser leídos.
4.2.1 Matrices en programación, Arreglos – Ejercicios resueltos en Python
[ejercicios resueltos] [ videos tutoriales] [ejercicios para resolver]
…
Ejercicios resueltos
Ejercicios resueltos sobre matrices en arreglos de dos dimensiones en Python y Numpy.
1) 3Eva_IT2002_T1 Triunfos, empates y derrotas por Goles
Solución propuesta: s3Eva_IT2002_T1 Triunfos, empates y derrotas por Goles
2) 3Eva_IT2000_T2 Matriz: puntos por goles en campeonato
Solución propuesta: s3Eva_IT2000_T2 Matriz: puntos por goles en campeonato
3) 3Eva_IT2003_T2 Verificar un cuadrado mágico
Solución propuesta: s3Eva_IT2003_T2 Verificar un cuadrado mágico
4) 2Eva_IT2009_T3 Mejores vendedores por categoría
Solución propuesta: s2Eva_IT2009_T3 Mejores vendedores por categoría
5) 1Eva_IIT2003_T3 Personas asignadas a proyectos
Solución propuesta: s1Eva_IIT2003_T3 Personas asignadas a proyectos
6) 2Eva_IIT2007_T2 Juego de memotest
Solución propuesta: s2Eva_IIT2007_T2 Juego de memotest , m_pdf
…
[ejercicios resueltos] [ videos tutoriales] [ejercicios para resolver]
Tutoriales de Matrices y arreglos
Ejercicios para Álgebra y Métodos Numéricos:
Unidad 3 Solución a sistemas de ecuaciones
Ejemplos en el curso de Métodos numéricos
…
[ejercicios resueltos] [ videos tutoriales] [ejercicios para resolver]
Ejercicios para resolver
Ejercicios de matrices en programación y su aplicación como arreglos de dos dimensiones.
3Eva_IT2000_T2 Matriz: puntos por goles en campeonato
2Eva_IIT2011_T3 Movimientos del caballo en ajedrez
3Eva_IIT2015_T3 funciones matrices rotar, extraer
3Eva_IIT2015_T4 Orientar código QR (Quick Response Code)
Matrices y Aleatorios
3Eva_IIT2014_T1 Ubicar estudiantes en aula
2Eva_IT2015_T3 Distribuye tortugas en región
2Eva_IT2015_T4 Movilidad de tortugas en región
Matrices en Álgebra
2Eva_IIT2009_T2 Transponer una matriz
4.2 Matrices en programación – Arreglos de dos dimensiones en Python
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
Las matrices en programación se manejan como arreglos de Numpy.
La interpretación de los datos de una Matriz o arreglo puede ser desde un sistema de ecuaciones, una tabla de goles de un campeonato o una hoja de calendario.
Al igual que los vectores, las matrices en arreglos tienen como componentes: «nombre», «índice» y «tamaño». Los valores de tamaño dependen de las dimensiones de la matriz. Para los primeros ejercicios serán rectangulares de nxm.
Los índices a diferencia de el álgebra, inician en cero.
En los ejercicios, la matriz de dos dimensiones usa como índices de filas la variable «i» y para columnas «j».
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
Matrices en programación con Numpy-Python
Para un mejor manejo de matrices en programación, se usan las funciones de la librería Numpy (Numerical Python) que se incorporan en el bloque de inicio con el alias np.
import numpy as np
Definir una matriz de nxm, con ceros o llena de unos, requiere la instrucción:
>>> import numpy as np >>> n = 5 >>> m = 7 >>> matriz0 = np.zeros(shape=(n,m), dtype=float) >>> matriz0 array([[0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0., 0.]]) >>> matriz1 = np.ones(shape=(n,m), dtype=float) >>> matriz1 array([[1., 1., 1., 1., 1., 1., 1.], [1., 1., 1., 1., 1., 1., 1.], [1., 1., 1., 1., 1., 1., 1.], [1., 1., 1., 1., 1., 1., 1.], [1., 1., 1., 1., 1., 1., 1.]]) >>>
El tipo de matriz (dtype=int) se añade para indicar que la matriz tiene datos tipo entero, la forma predeterminada para los datos es tipo real (dtype=float)
Las dimensiones de la matriz se obtienen mediante la instrucción con Numpy:
>>> np.shape(matriz0) (5, 7) >>> tamano = np.shape(matriz0) >>> tamano (5, 7) >>> tamano[0] 5 >>> tamano[1] 7 >>> dimension = np.ndim(matriz0) >>> dimension 2 >>>
entre otras operaciones en Numpy que reflejan las operaciones de matrices de álgebra.
Referencias: Inicie con la definición de matrices del álgebra lineal:
http://blog.espol.edu.ec/matg1049/cl1-02-sistema-de-ecuaciones-lineales/
Las operaciones básicas de matrices se describen también en álgebra lineal:
http://blog.espol.edu.ec/matg1049/cl2-07-operaciones-entre-subespacios/
Algoritmos sobre Matrices en Análisis y Métodos Numéricos
La Unidad 3 Sistemas de Ecuaciones del curso Análisis Numérico desarrolla los algoritmos en Python en base a los métodos matemáticos.
Interpretación de matrices
Observe el siguiente video y plantee la relación con el tema de arreglos, matrices, dimensiones y computación.
Las aplicaciones de las matrices | Lo que desearía que mis maestros me hubieran dicho antes. Zach Star. 11 oct 2019.
Arreglos: [ índice ][ Vector ] [ Matriz ] || [ cadenas/string ] [listas]
4.1.1 Vectores como arreglos en programación Arreglos – Ejercicios resueltos en Python
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
…
Ejemplo 1 – Secuencia de Fibonacci
Referencia: Ejercicio 12 de 3.3.3 Tarea-Lazos
La secuencia de Fibonacci es muy reconocida en la matemática. Como introducción al tema se recomienda observar el video de «misterio de las matemáticas» que tiene una explicación interesante entre los tiempos 2:33 y 6:40, por lo que el video inicia en el minuto 2:33.
La secuencia se desarrolla a partir de dos números: 1 y 1
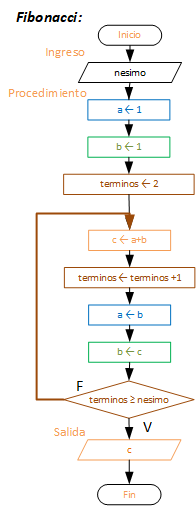
El siguiente término se obtiene sumando los dos anteriores:
1 1 2 3 5 8 13 21 ...
a+b=c
a+b=c
a+b=c
El algoritmo primero se presenta en el diagrama de flujo para facilidad visual de los pasos.
Al requerir mostrar toda la secuencia, en lugar de un solo valor, aparece la necesidad de usar un vector.
Para éste caso usamos la librería numpy para obtener los siguientes resultados:
¿cuál término?: 8 término n-ésimo: 21 secuencia: [ 1 1 2 3 5 8 13 21] >>>
Algoritmo en Python
Se modifican las instrucciones para añadir la secuencia en un vector:
# secuencia de fibonacci # usando vectores import numpy as np # INGRESO nesimo = int(input('¿cuál término?: ')) # PROCEDIMIENTO a = 1 b = 1 terminos = 2 secuencia = np.zeros(nesimo,dtype = int) secuencia[0] = 1 secuencia[1] = 1 while not(terminos>=nesimo): c = a+b secuencia[terminos] = c terminos = terminos+1 a = b b = c # SALIDA print('término n-ésimo: ',c) print('secuencia: ', secuencia)
Ejemplo 2: 1Eva_IIT2015_T3 Vector de números primos
Primero desarrolle el algoritmo para un número cualquiera «n«.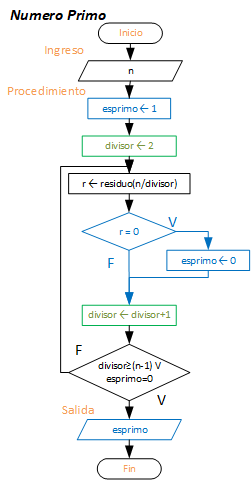 
Como hipótesis, inicie considerando que el número es primo, esprimo=1, luego pruebe con cada uno de los divisores en el intervalo entre 2 y (n-1).
La divisibilidad se revisa con el residuo entre el número n y los divisiores del intervalo [2,n-1].
Primero con divisor=2. El número 1 no cuenta pues todos los números son divisibles para 1.
Si el residuo calculado tuvo resultado cero, el número n no es primo, esprimo=0. Continua las pruebas con el siguiente divisor, divisor = divisor +1
Se revisa si se han probado con todos los números inferiores a n o que el resultado ya no es primo, esprimo=0.
Se muestran los resultados.
El esquema del ejemplo se muestra en el diagrama de flujo.
Algoritmo en Python
Convirtiendo las instrucciones de diagrama de flujo a instrucciones en Python:
# 1ra Evaluación II Término 2015. Tema 3 # numeros primos # INGRESO n = int(input('primo a revisar: ')) # PROCEDIMIENTO ES PRIMO esprimo = 1 divisor = 2 while not(divisor>=(n-1) or esprimo==0): residuo = n%divisor if (residuo==0): esprimo=0 divisor = divisor+1 # SALIDA print('numero primo: ', esprimo)
Tarea
En una secuencia de números enteros, identifique cuales son números primos.
Reutilice el algoritmo anterior para almacenar cada resultado en un vector, indicando 1 si es primo y 0 si no lo es.
Luego de probar que el algoritmo funciona, realice un bloque de ingreso para la secuencia de prueba.
numeros prueba: [ 2 3 4 5 6 7 8 9 10] cumple esprimo: [ 1 1 0 1 0 1 0 0 0] >>>
# 1ra Evaluación II Término 2015 # numeros primos import numpy as np # INGRESO probar = np.array([2,3,4,5,6,7,8,9,10]) # PROCEDIMIENTO tamano = len(probar) cumple = np.ones(tamano, dtype=int) posicion = 0 while not(posicion==tamano): n = probar[posicion] # PROCEDIMIENTO ES PRIMO esprimo = 1 i = 2 while not(i>=(n-1) or esprimo==0): r = n%i if (r==0): esprimo=0 i = i+1 cumple[posicion] = esprimo posicion = posicion+1 # SALIDA print('numeros prueba: ', probar) print('cumple esprimo: ', cumple)
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
…
Ejercicios resueltos de vectores como arreglos en Python
Vectores – Arreglos unidimensionales con Python y Numpy
1Eva_IT2013_T4 Tabular atención al cliente
solución propuesta: s1Eva_IT2013_T4 Tabular atención al cliente
1Eva_IIT2002_T2 Color de placas de vehículos
solución propuesta: s1Eva_IIT2002_T2 Color de placas de vehículos
1Eva_IT2008_T2 Criba de Eratóstenes
solución propuesta: s1Eva_IT2008_T2 Criba de Eratóstenes
1Eva_IT2002_T3 Calificaciones mejores que alguien
Arreglos unidimensionales y números aleatorios
1Eva_IT2008_T3 Simular precio de petroleo
Solución literal c: s1Eva_IT2008_T3 Simular precio de petroleo
1Eva_IIT2010_T3 Juego del amigo secreto
Solución propuesta: s1Eva_IIT2010_T3 Juego del amigo secreto
1Eva_IIT2007_T2 Juego de la Ruleta
Solución propuesta: s1Eva_IIT2007_T2 Juego de la Ruleta
Arreglos, acumuladores y contadores
1Eva_IIT2010_T1 Censo de instrucción por género
Solución propuesta: s1Eva_IIT2010_T1 Censo de instrucción por género
1Eva_IT2011_T3 Calcular ventas por región
Solución propuesta: s1Eva_IT2011_T3 Calcular ventas por región
Solución propuesta: s1Eva_IT2013_T1 Primos gemelos
1Eva_IT2008_T2 Criba de Eratóstenes
Solución propuesta: s1Eva_IT2008_T2 Criba de Eratóstenes
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
Ejercicios para resolver sobre de arreglos en programación
1Eva_IT2005_T3 Arreglo aleatorio binario a decimal
1Eva_IT2001_T6 Piloto y copiloto para nave
1Eva_IIT2002_T3 Conjetura de Ullman
1Eva_IIT2008_T4 Área del polígono convexo por triángulos
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]