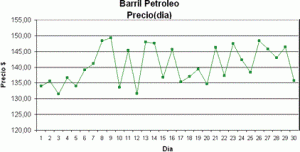
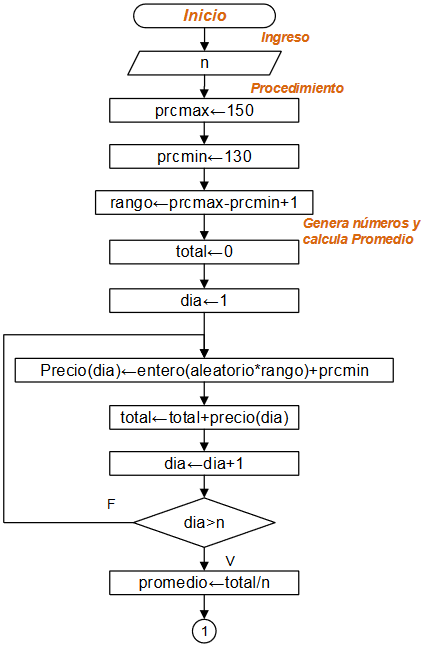
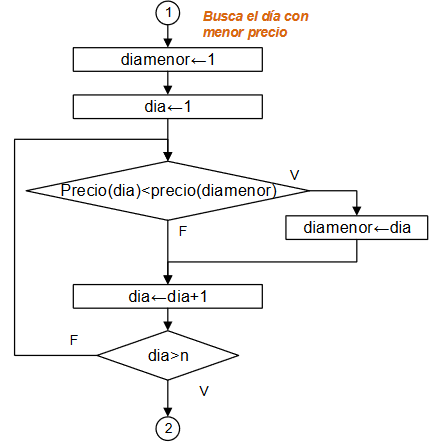
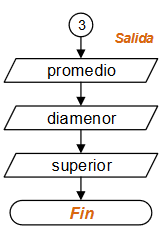
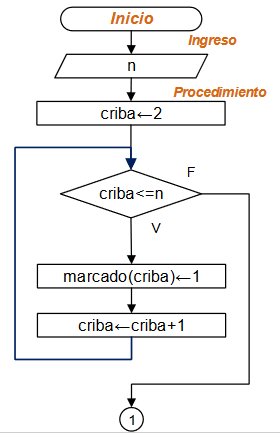
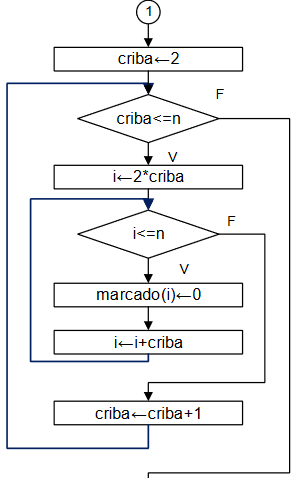
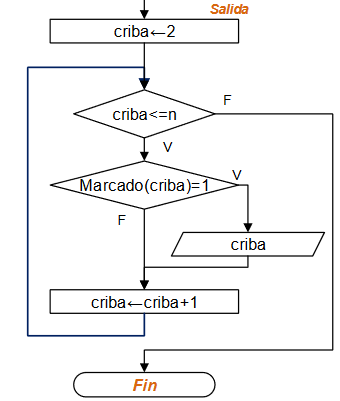
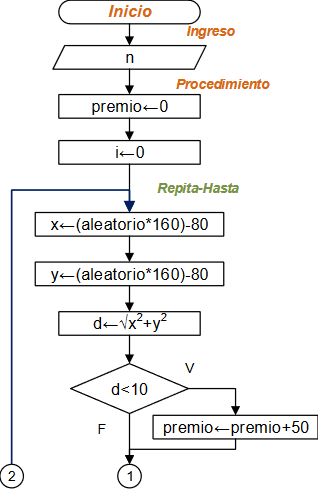
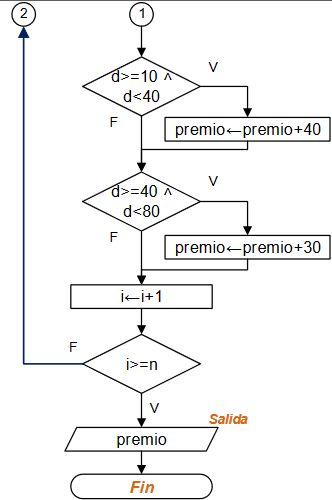
Ejercicio: 1Eva_IIT2007_T1 Hormiga busca arroz
Propuesta de solución en Python: python.pdf, también en versión matlab.pdf.
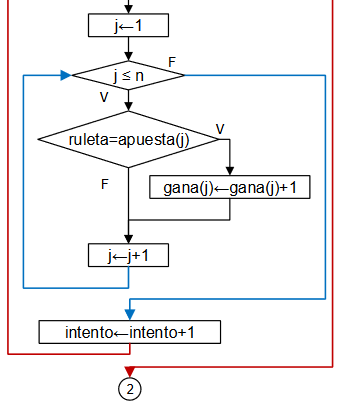
Algoritmo con un paso por cada turno
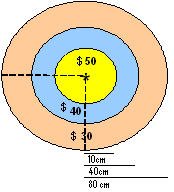
Considere ingresar la ubicación inicial (xh,yh) de la hormiga y que la posición del arroz (xa,ya) sea fija.
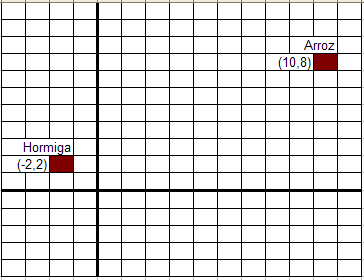Suponga que la distancia inicial es la mayor y que la hormiga no ha encontrado el grano de arroz.
Para la dirección del movimiento de la hormiga y la cantidad de pasos se generan números aleatorios cuyos valores se usan para simular el movimiento al cambiar las coordenadas de la hormiga.
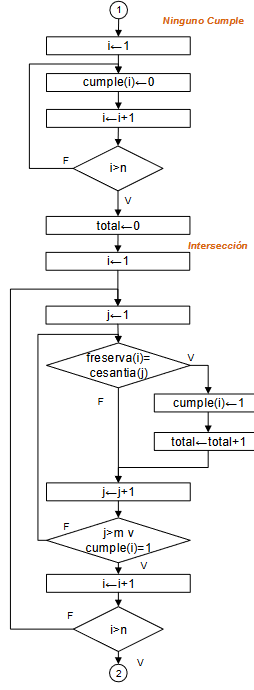
Luego de cada movimiento, se revisa si la hormiga encontró el grano de arroz o que las coordenadas sean iguales; también se puede revisar si la nueva distancia es mayor a las anteriores.
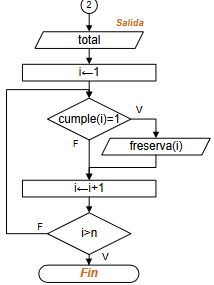
Cuente un turno completado, y repita el procedimiento hasta que se completen los 100 turnos o se haya encontrado el grano de arroz. Al final muestre los resultados buscados.
# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2007_T1 Hormiga busca arroz
import random as rnd
# INGRESO
xa=int(input(' x arroz: '))
ya=int(input(' y arroz: '))
xh=int(input(' x hormiga: '))
yh=int(input(' y hormiga: '))
# PROCEDIMIENTO
encontro = 0
t = 0
while not((xh==xa and yh==ya) or t>100):
# dirección de movimiento de hormiga
d = int(rnd.random()*4)+1
if (d==1):
yh = yh+1
if (d==2):
yh = yh-1
if (d==3):
xh = xh+1
if (d==4):
xh = xh-1
# Revisa si lo encontró
if (xh==xa and yh==ya):
encontro = 1
t = t + 1
print('¿encontró?: ')
print(encontro)
print('pasos realizados: ')
print(t)
Ejemplo de respuesta con el algoritmo
x arroz: 5
y arroz: 3
x hormiga: 4
y hormiga: 2
¿encontró?:
1
pasos realizados:
34
>>>
x arroz: 8
y arroz: 8
x hormiga: 3
y hormiga: 2
¿encontró?:
0
pasos realizados:
101
Algoritmo con varios pasos por turno
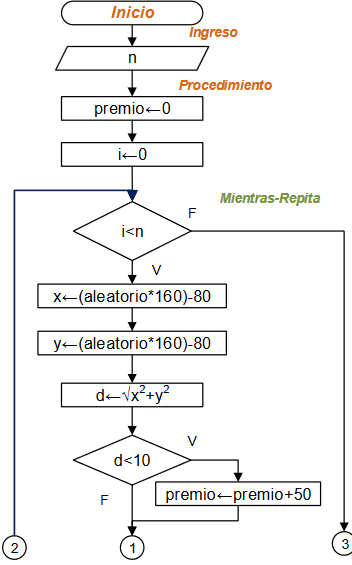
En la solución con Python, se usarán las librerías básicas de aleatorios (random) y matemáticas (math).
Una alternativa a esta solución es usar la librería numérica NUMPY, que se descarga e instala como un módulo complementario.
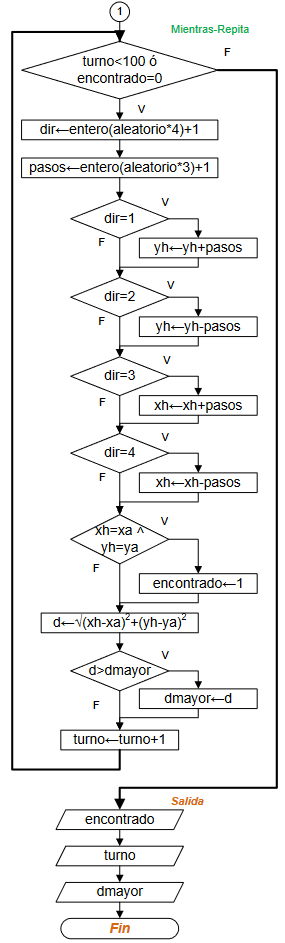
Usando lazo Mientras-Repita:
# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1ra Eval II Termino 2007. Tema 1. Hormiga y arroz
# Propuesta de solución. edelros@espol.edu.ec
import random as rnd
import math
xh = int(input('coordenada x hormiga: '))
yh = int(input('coordenada y hormiga: '))
# PROCEDIMIENTO
# posición del arroz fija
xa = 10
ya = 8
# distancia inicial
dmayor = math.sqrt((xh-xa)**2+(yh-ya)**2)
encontrado = 0
turno = 0
while (turno<100 and encontrado==0):
direccion = int(rnd.random()*4)+1
pasos = int(rnd.random()*3)+1
if direccion==1:
yh = yh + pasos
if direccion==2:
yh = yh - pasos
if direccion==3:
xh = xh + pasos
if direccion==4:
xh = xh - pasos
if (xh==xa and yh==ya):
encontrado = 1
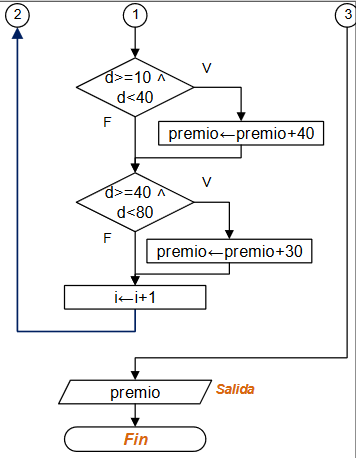
distancia = math.sqrt((xh-xa)**2+(yh-ya)**2)
if distancia>dmayor:
dmayor = distancia
turno = turno + 1
# SALIDA
print('estado encontrado: ')
print(encontrado)
print('turnos simulados: ')
print(turno)
print('distancia más lejana: ')
print(dmayor)
Reaultado del algoritmo:
coordenada x hormiga: 2
coordenada y hormiga: 1
estado encontrado:
1
turnos simulados:
92
distancia más lejana:
23.323807579381203
>>>
coordenada x hormiga: 0
coordenada y hormiga: 0
estado encontrado:
0
turnos simulados:
100
distancia más lejana:
38.2099463490856
>>>
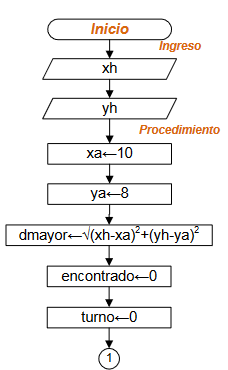
Usando lazo Repita-Hasta:
# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1ra Eval II Termino 2007. Tema 1. Hormiga y arroz
# Propuesta de solución. edelros@espol.edu.ec
import random as rnd
import math
xh = int(input('coordenada x hormiga: '))
yh = int(input('coordenada y hormiga: '))
# PROCEDIMIENTO
# posición del arroz fija
xa = 10
ya = 8
# distancia inicial
dmayor = math.sqrt((xh-xa)**2+(yh-ya)**2)
encontrado = 0
turno = 0
while not(turno>=100 or encontrado!=0):
direccion = int(rnd.random()*4)+1
pasos = int(rnd.random()*3)+1
if direccion==1:
yh = yh + pasos
if direccion==2:
yh = yh - pasos
if direccion==3:
xh = xh + pasos
if direccion==4:
xh = xh - pasos
if (xh==xa and yh==ya):
encontrado = 1
distancia = math.sqrt((xh-xa)**2+(yh-ya)**2)
if distancia>dmayor:
dmayor = distancia
turno = turno+1
# SALIDA
print('estado encontrado: ')
print(encontrado)
print('turnos simulados: ')
print(turno)
print('distancia más lejana: ')
print(dmayor)
ejercicios resueltos Python 1eva_iit2007_t1 pdf
ejercicios resueltos Matlab 1eva_iit2007_t1 pdf
