Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
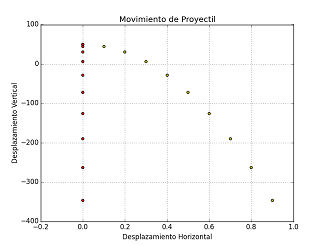
Diapositivas: Graficando tiempo vs distancia, velocidad y aceleración.
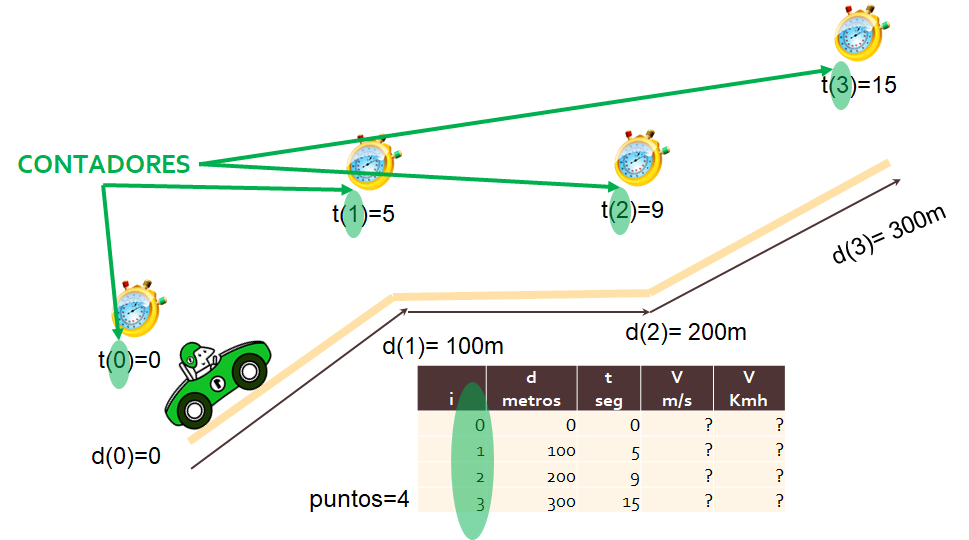
Situación propuesta: Observar en una gráfica los datos del ejercicio anterior.
Tomar lecturas de distancias y tiempos recorridos, para obtener velocidades por tramo en Kmh
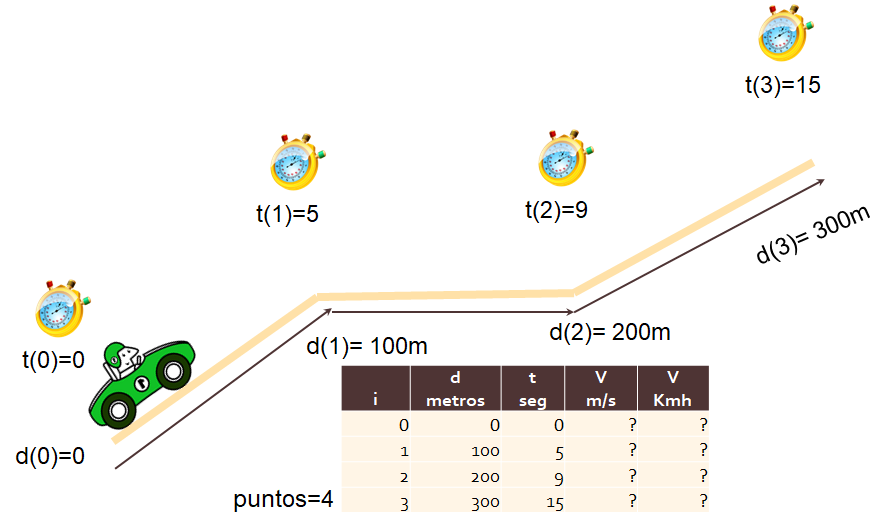
Usaremos los resultados del ejercicio: velocidadtramos.py
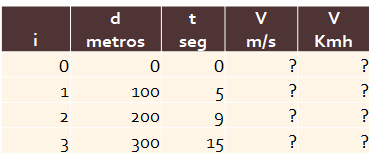
Ejecutar el archivo con los datos del problema mostrado para obtener en memoria los resultados siguientes mostrados.
>>> d
array([ 0., 100., 200., 300.])
>>> t
array([ 0, 5, 9, 15])
>>> v
array([ 0. , 20. , 25. , 16.66666667])
>>> vkmh
array([ 0., 72., 90., 60.])
>>>
1. Gráfica desde linea de instrucciones
Se puede crear la gráfica paso a paso desde el Shell de
Python
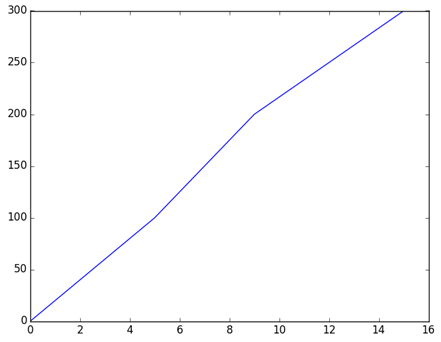
Se requiere importar la librería para gráficas con el álias “plt” que es estandarizado.
>>> import matplotlib.pyplot as plt
Se crea la línea a graficar
>>> plt.plot(t,d)
Mostrar el gráfico construido
>> plt.show()
2. Añadir títulos de gráfico
>>> import matplotlib.pyplot as plt
Usar la forma interactiva para generar el gráfico, No se usa en el script
>>> plt.ion()
>>> plt.plot(t,d)
[<matplotlib.lines.Line2D object at 0x05A605F0>]
>>> plt.title('Distancia recorrida vs tiempo acumulado')
<matplotlib.text.Text object at 0x05A50630>
>>> plt.xlabel('tiempo segundos')
<matplotlib.text.Text object at 0x05A0A910>
>>> plt.ylabel('distancia en metros')
<matplotlib.text.Text object at 0x05A3C430>
Desconetar la interactiva con plt.ioff() y en el script:
>>> plt.show()
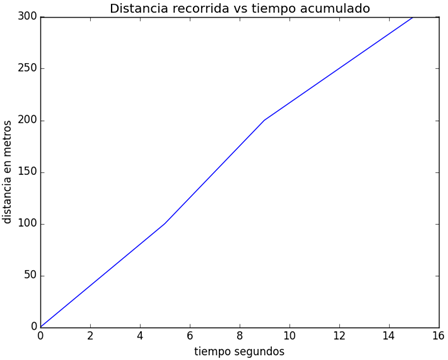
3. Colores y marcas de punto
Nos permiten realizar las gráficas de datos disponibles en un arreglo.
Se utiliza: plt.plot ( x, y, propiedades);
Las propiedades como el color y el punto se especifican entre apóstrofes:
| Letra |
Color |
|
Símbolo |
forma |
| b |
Blue (azul) |
|
. |
Punto |
| g |
Green(verde) |
|
o |
círculo |
| r |
Red (rojo) |
|
x |
Marca de X |
| y |
Yellow (amarillo) |
|
+ |
Marca de + |
| k |
Black (negro) |
|
s |
cuadro |
| w |
White(blanco |
|
v |
Triángulo |
| m |
magenta |
|
o |
pentagrama |
las instrucciones a usar son:
>>> plt.plot(t,v,'ro-')
[]
>>> plt.title('velocidad observada vs tiempo acumulado')
>>> plt.xlabel('tiempo en segundos')
>>> plt.ylabel('velocidad en m/s')
>>> plt.show()
con lo que se obtiene

Taller – Aceleración media
Referencia: Física Universitaria Sears –Zemanski. Vol 1. Edición 12. Ejercicio 2.12
(2.12). Un piloto de pruebas de Automotores Galaxia, S.A., está probando un nuevo modelo de automóvil con un velocímetro calibrado para indicar m/s en lugar de mi/h. Se obtuvo la siguiente serie de lecturas durante una prueba efectuada en una carretera recta y larga:
| tiempo(s) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
| Rapidez(m/s) |
0 |
0 |
2 |
6 |
10 |
16 |
19 |
22 |
22 |
a) Calcule la aceleración media en cada intervalo de 2 s.
¿La aceleración es constante? ¿Es constante durante alguna parte de la prueba?
b) Elabore una gráfica vx – t con los datos, usando escalas de 1 cm = 1 s horizontalmente, y 1 cm = 2 m/s verticalmente.
Dibuje una curva suave que pase por los puntos graficados.
Mida la pendiente de la curva para obtener la aceleración instantánea en: t =9 s, 13 s y 15 s.
Desarrollar el literal a) en Python
tiempo = [0.0, 2, 4, 6, 8, 10, 12, 14, 16]rapidez = [0, 0, 2, 6, 10, 16, 19, 22, 22]
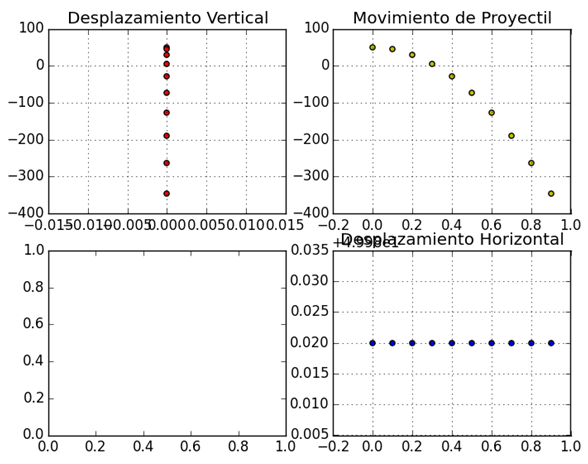
4. Subgráficos (subplots)
Permiten realizar grupos de gráficos en un esquema tipo matricial.
gráfica, cuadro=plt.subplots(2) 
El índice del primer cuadro es el cer0
cuadro[0].plot(x,y)
El siguiente cuadro es el uno
cuadro[1].step(tiempo,acelera,’r’)
Se pueden añadir o cambiar las propiedades de un cuadro:
cuadro[0].set_title(‘tiempo vs rapidez’)
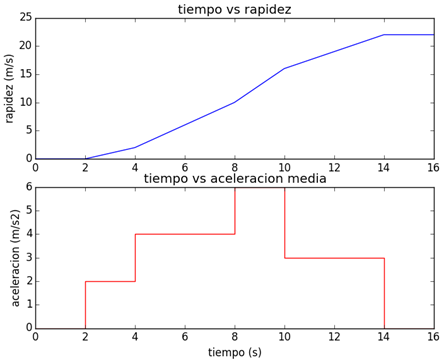
Las instrucciones en Python desde la toma de datos son
# FCNM-ESPOL. Física con python
# calcular aceleracion media por intervalo
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
puntos = int(input('¿puntos observados?:'))
tiempo = np.zeros(puntos,dtype=int)
rapidez = np.zeros(puntos,dtype=float)
i = 0
while (i<puntos):
tiempo[i] = int(input('tiempo transcurrido (s):'))
rapidez[i] = float(input('distancia recorrida (m/s):'))
i = i + 1
# PROCEDIMIENTO
acelera = np.zeros(puntos,dtype=float)
i = 0
acelera[0] = 0
i = 1
while (i<puntos):
acelera[i] = rapidez[i]-rapidez[i-1]
i = i + 1
En el bloque de salida se puede añadir:
#grafica con dos cuadros
grafica,cuadro = plt.subplots(2)
cuadro[0].plot(tiempo,rapidez)
cuadro[0].set_title('tiempo vs rapidez')
cuadro[0].set_ylabel('rapidez (m/s)')
cuadro[1].step(tiempo,acelera,'r')
cuadro[1].set_title('tiempo vs aceleracion media')
cuadro[1].set_xlabel('tiempo (s)')
cuadro[1].set_ylabel('aceleracion (m/s2)')
plt.show()