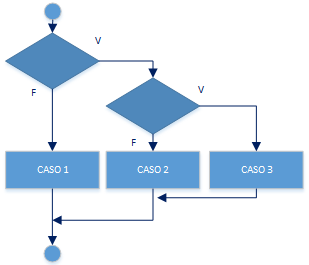
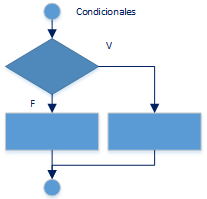
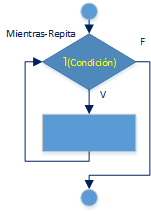
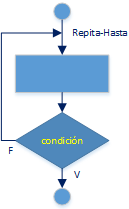
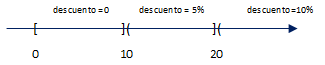---

---

Ejercicios resueltos en Python y diagramas de flujo como ejemplos de las estructuras de control para condicionales if else (selección).

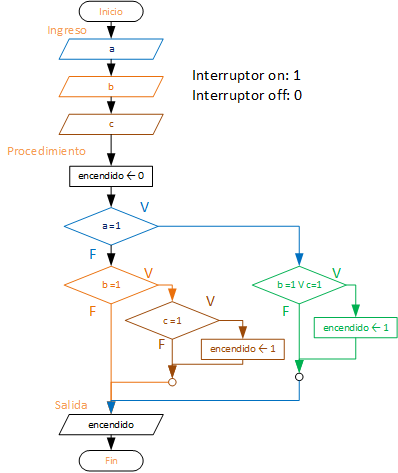
1. Ejercicio 6. interruptores para encender un foco

En un circuito eléctrico hay tres interruptores, los cuales pueden estar en estado cerrado(1) o abierto(0).

Para que un equipo funcione, se requiere que al menos dos estén cerrados. Si los datos son el estado de los interruptores, determine si el equipo funcionará.

Desarrollo:
Al inicio, supone que el foco no está encendido (0) .

Instrucciones en Python

# Ejercicio 6. Interruptores y un foco

# INGRESO
a = int(input('interruptor a: '))
b = int(input('interruptor b: '))
c = int(input('interruptor c: '))

# PROCEDIMIENTO
encendido = 0
if (a==1):
    if (b==1 or c ==1):
        encendido = 1
else:
    if (b==1):
        if (c==1):
            encendido = 1
# SALIDA
print('estado del foco: ',encendido)

Escriba otras propuestas de solución.

---

---

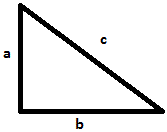
2. Ejercicio 12. Bloque rectangular pasa por orificio en pared.

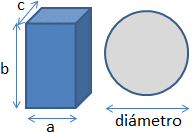
Lea las tres dimensiones de un bloque rectangular.

Encuentre las tres diagonales de sus caras diferentes y determine si pudiera atravesar por un orificio circular de diámetro dado.

Nota: Para el desarrollo considere usar la diagonal de cada lado, que es la parte de mayor longitud que debe pasar por el diámetro del círculo.

 

Instrucciones en Python

# Problema de la caja y el orificio en la pared
import numpy as np

# INGRESO
a = float(input("lado a: "))
b = float(input('lado b: '))
c = float(input('lado c: '))
d = float(input('lado d: '))

# PROCEDIMIENTO
diagonal1 = np.sqrt(a**2 + c**2)
diagonal2 = np.sqrt(a*a + b*b)
diagonal3 = np.sqrt(b*b + c*c)

pasa = 0
if (diagonal1<d):
    pasa = 1
if (diagonal2<d):
    pasa = 1
if (diagonal3<d):
    pasa = 1

# SALIDA
print(pasa)

Tarea: Realizar diagrama de Flujo. Desarrollado en Pizarra durante la clase

---

---

---

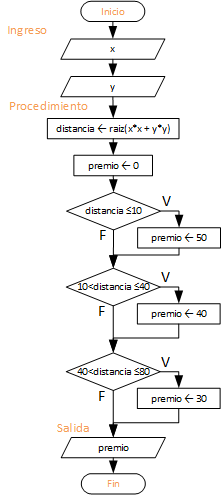
3. Ejercicio: 1Eva2007TI_T1 Tiro al blanco con dardos

Desarrollado para la primera semana de clases.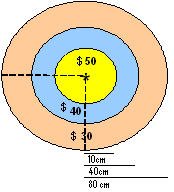

Considere solo la parte de condicionales, a partir del ingreso de las coordenadas x,y donde cae el dardo.

Instrucciones en Python

# Un dardo en tablero
# 1ra Evaluación I Término 2007. Tema 1
import numpy as np

# INGRESO
x = float(input('coordenada x: '))
y = float(input('coordenada y: '))

# PROCEDIMIENTO
distancia = np.sqrt(x**2 + y**2)
premio = 0
if (distancia <= 10):
    premio = 50
if (distancia>10 and distancia<=40):
    premio = 40
if (distancia>40 and distancia<=80):
    premio = 30

# SALIDA
print('el premio obtenido es: ', premio)

---

---

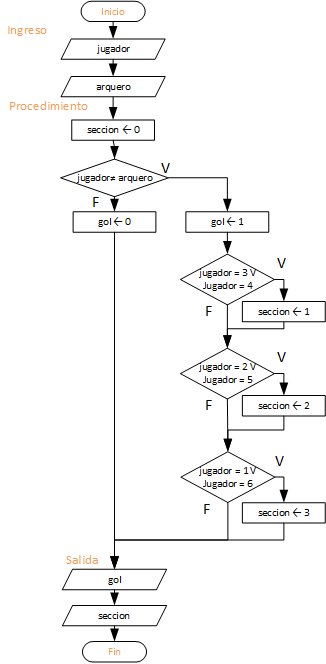
4. Ejercicio 1Eva_IT2005_T4 Lanza penales

Desarrollado para un solo penal.
Dado el sector del arco [1,6] donde un jugador lanza el balón y el sector donde el arquero protege, determinar: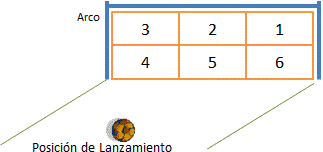

a) si hubo gol (1 ó 0)

b) si hubo gol, indicar si fué por izquierda (1), centro(2), derecha(3)

Se inicia considerando que no hubo gol, por lo que la sección=0 para el área donde entró el gol. Hay gol si jugador ≠ jugador.

Diagrama de Flujo

Instrucciones en Python

# analizar un penal
# Parcial I Término 2005. Tema 4.

# INGRESO
jugador = int(input('sector del jugador:'))
arquero = int(input('sector del arquero:'))

# PROCEDIMIENTO
seccion = 0
if not(jugador==arquero):
    gol = 1
    if (jugador==3 or jugador==4):
        seccion = 1
    if (jugador==2 or jugador==5):
        seccion = 2
    if (jugador== 1 or jugador==6):
        seccion = 3
else:
    gol = 0

# SALIDA
print('Hubo gol: ',gol)
print('seccion: ', seccion)

---

---

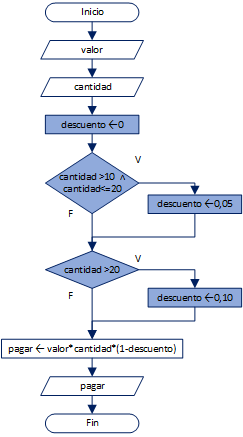
5. Ejercicio Tarea 1 ejercicio 3. Ganancia sobre costo

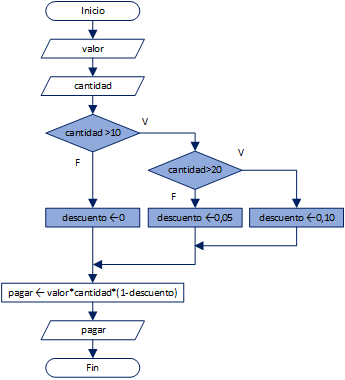
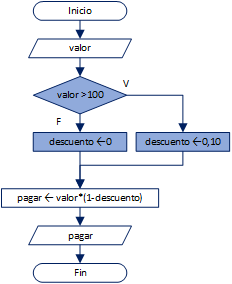
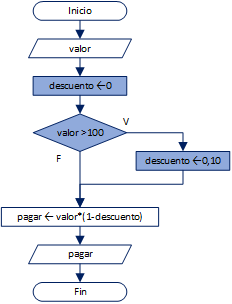
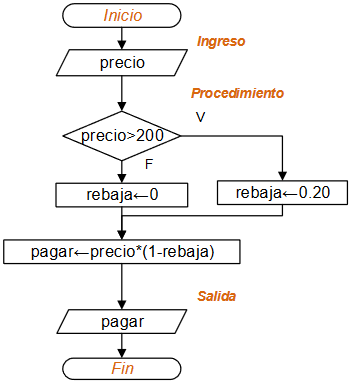En un almacén se descuenta 20% del precio al cliente si el valor a pagarse es mayor a $200.

Dado un valor de precio, muestre lo que debe pagar el cliente.

ejercicios resueltos Python Tarea1Ejercicio1y3 pdf

 

---

---

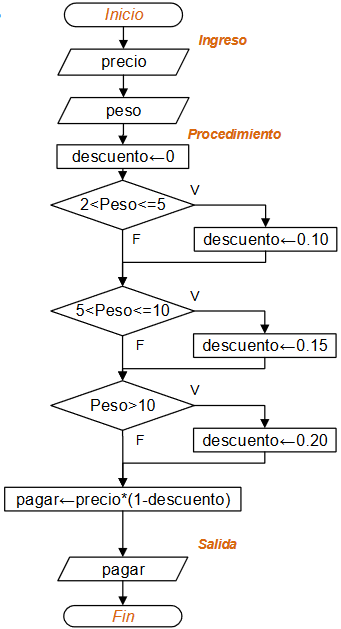
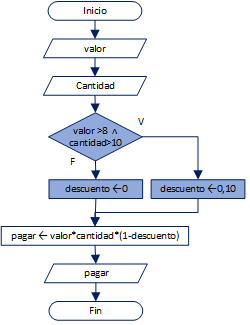
6. Ejercicio Tarea 1 ejercicio 5. Aplicar descuentos en compras al por mayor

Una frutería ofrece las manzanas con descuento según la siguiente tabla: Dado el precio por kilo, y el peso, determinar cuánto pagará una persona que compre manzanas es esa frutería.	kilos comprados	Descuento %
	0 - 2	0%
	2.01 - 5	10%
	5.01 - 10	15 %
	10.01 en adelante	20%

ejercicios resueltos Python tarea1ejercicio5 pdf

---

---

---

---

Condicionales "if-else" múltiple o con varios casos

Referencia: Van Rossum 4.1 p19, Rodríguez 3.5 p42, Downey 5.7

Existen problemas en los que una variable puede tomar diferentes valores conforme al cumplimiento de diferentes condiciones o casos.

Un ejemplo es cuando se realizan ventas por volumen, el descuento depende de la cantidad del producto que se vende.

Cuando la variable resultado del condicional puede tener varios valores, se puede adoptar una forma simple del problema al dividirla por casos, empezando por el caso básico y se modifica la variable resultado lo modifica cuando se revisan los casos siguientes.

Para estos casos se usan estructuras de control para selección en forma anidada en forma de serie o en forma de árbol.

---

---

Condicionales múltiples en serie

Ejemplo 3. Un almacén rebaja 10% del precio de un producto si se adquieren más de 20 unidades y 5% si adquieren hasta 20 unidades pero más de 10, no hay descuento para cantidades menores o iguales a 10 unidades.

Con el precio unitario del producto y la cantidad adquirida, realice un algoritmo para mostrar el valor a pagar.

 

 

Desarrollo:

Para seguir una forma ordenada del problema, se dividen los casos de cantidad en segmentos de recta numérica.

El aplicar los descuentos consiste en evaluar los intervalos de cantidad y escribirlos como casos con condicionales.

Las instrucciones de condicionales en Python se muestran como:

# Ejemplo 3.Descuentos en productos por precio y cantidad.

# Ingreso
valor = float(input('Valor del producto: '))
cantidad = float(input('cantidad del producto: '))

# Procedimiento
descuento = 0
if (cantidad > 10 and cantidad<=20):
    descuento = 0.05
if(cantidad > 20):
    descuento = 0.10

pagar = valor*cantidad*(1-descuento)

# Salida
print(pagar)

---

---

Condicionales múltiples en árbol

Otra forma de resolver el problema del ejemplo anterior, consiste en generar un camino por cada caso para asignar el valor a la variable de salida.

Cada camino es parte de un condicional.

Siguiendo ésta idea, el diagrama de flujo anterior se reorganiza y muestra como:

Las instrucciones en Python sobre condicionales para el ejercicio son:

# Ejemplo 3.Descuentos en productos por precio y cantidad.

# Ingreso
valor = float(input('Valor del producto: '))
cantidad = float(input('cantidad del producto: '))

# Procedimiento
descuento = 0
if (cantidad>10):
    if (cantidad<=20):
        descuento = 0.10
    else:
        descuento = 0.05
else:
    descuento = 0.0

pagar = valor*cantidad*(1-descuento)

# Salida
print(pagar)

Referencia: Elementos esenciales para programación: Algoritmos y Estructuras de Datos Latin Project. Primera Edición 2014. Sección 4.1.2 p.66

---

---

---

---

Condicionales "if-else" - Estructura de selección

Referencia: Van Rossum 4.1 p19, Rodríguez 3.4.1 p26, Downey 5.5

Las estructuras de selección son un tipo de estructuras de control que permiten decidir que acción seguir a partir de una condición.

Cuando se puede escoger entre dos caminos, se debe tomar una decisión entre las opciones. En estos casos se utilizan los "Condicionales" que son estructuras de selección.

El condicional más simple está conformado por solo dos caminos, se formula una pregunta simple que compara al menos dos variables mediante expresiones de comparación, tales como:

a=b	a>b	a<b
a<=b	a>=b	etc...

El condicional en diagramas de flujo se representa por un rombo, la expresión se escribe dentro del rombo. Por convención, hacia la derecha del rombo se grafica el caso que la expresión resultada verdadera (V), y hacia abajo o la izquierda se grafica la acción cuando el resultado es falso (F) Una forma de recordar esta convención es extender la mano derecha en señal de verdad, y al extender la mano izquierda, nos queda el lado el lado falso.

Para mostrar la aplicación de un condicional en un algoritmo se utilizan los siguientes ejemplos:

---

Ejemplo 1. Condicionales para aplicar descuentos

Un almacén aplica un descuento del 10% a quienes han comprado en productos más de 100 dólares. Realice un algoritmo que permita realizar esta operación directamente en la caja registradora. Desarrollo: El descuento lo puede aplicar el cajero, o se puede incorporar el algoritmo a la máquina registradora. La variable de ingreso es el valor de compra, el procedimiento debe determinar el valor a pagar, que se presenta al final como variable de salida. El diagrama de flujo que representa el algoritmo es el diagrama 1, las instrucciones en un archivo de Python se adjunta a continuación:

# Ejemplo 1.Descuentos en productos de precio alto.

# Ingreso
valor = float(input('Valor del producto: '))

# Procedimiento
if valor >100:
    descuento = 0.10
else:
    descuento = 0
pagar = valor*(1-descuento)

# Salida
print(pagar)

la ejecución el archivo Python:

Valor del producto: 120
108.0
>>>

Otra forma de expresar el algoritmo en diagrama de flujo, con el punto de vista del dueño del almacén, quien prefiere que no exista descuento inicia con cero (0) y se modifica solo si cumple con la condición de que adquiera más de 100 dólares (diagrama 2):

Las instrucciones en Python se escriben como:

# Ejemplo 1.Descuentos en productos de precio alto.

# Ingreso
valor = float(input('Valor del producto: '))

# Procedimiento
descuento = 0
if valor >100:
    descuento = 0.10
pagar = valor*(1-descuento)

# Salida
print(pagar)

En el caso que el condicional modifique una variable solo en el caso de cumplir una condición, no es necesario graficar una acción. En estos casos, se debe escribir la expresión en la forma que permita que el lado sin acción quede del lado falso.

---

---

Condicional con varias preguntas - Conectores and/or/not

Cuando se debe incluir más de una pregunta en un condicional, se utilizan los operadores lógicos.

En diagramas de flujo o seudo-código, las expresiones usan las mismas conectivas que en la notación de lógica matemática (and, or, not).

Conectiva	símbolo	operador
Conjunción	∧	and
Disyunción	∨	or
Negación	⌉	not( ) , !

---

Ejemplo 2. Condicional para aplicar descuentos por volumen o cantidad comprada.

Un almacén aplica el descuento del 15% para artículos de valor mayor a 8 dólares y que incluyan más de 10 artículos.

Desarrollo: Para el ejercicio se requieren dos variables de ingreso: valor y cantidad. El descuento se aplica con la expresión:

(valor > 8) ∧ (cantidad > 10)

Para el procedimiento se continúa de igual forma que en el ejercicio anterior:

Instrucciones en Python

# Ejemplo 2.Descuentos en productos de precio alto.

# Ingreso
valor = float(input('Valor del producto: '))
cantidad = float(input('cantidad del producto: '))

# Procedimiento
if (valor>8 and cantidad>10) :
    descuento = 0.10
else:
    descuento = 0

pagar = valor*cantidad*(1-descuento)

# Salida
print(pagar)

resultado del algoritmo:

Valor del producto: 10
cantidad del producto: 15
135.0
>>>

Referencia: Elementos esenciales para programación: Algoritmos y Estructuras de Datos Latin Project. Primera Edición 2014. Sección 4.1. p.62

---

---

[ Estructuras de control ] [ Condicional ] [ Bucle while ] [ Bucle for ]

..

---

Estructuras de Control en programación

Referencia: Van Rossum 4 p19, Rodriguez 3.4 p26, Downey 5.5

Las estructuras de control en programación permiten realizar acciones ordenadas en el algoritmo por bloques o secciones de instrucciones, facilitando la escritura y lectura.

Estructura Básica

Toda solución a un problema (algoritmo) puede ser planteado usando una estructura básica ordenada, compuesta por:

• Inicio
• ingreso
• procedimiento
• salida
• fin

Las estructuras de control se usan como una forma lógica y ordenada de plantear un algoritmo, para que sea legible por otras personas. Así el algoritmo también será modular semejante a las piezas de un Lego.

Los diagramas de flujo muestran de forma gráfica la estructura lógica y ordenada de un algoritmo.

Las estructuras o bloques se podrán reutilizar en otros algoritmos (funciones(variables)) para evitar escribirlos nuevamente y solo realizar llamadas sobre sus nombres y parámetros.

---

[ Estructuras de control ] [ Condicional ] [ Bucle while ] [ Bucle for ]

---

Bloque de Inicio en Python

Permite dar las indicaciones iniciales para la solución de un problema, tales como la referencias o comentarios (#), traer o importar las herramientas, conocidas como librerías , definir sus propias herramientas (funciones), etc.

comentarios o referencias:

# 1ra Eval. II Termino 2014
# Tema 1

Librerías para cálculo numérico, por ejemplo: Numpy

import numpy as np
c = np.sqrt((a**2)+(b**2))

Librerías para uso de aleatorios: random

import random as rnd
dado = int(rnd.random.random()*6)+1

Librerías para uso de vectores y Matrices: Numpy

import numpy as np
tabla= np.zeros(5,dtype=int)
tabla= np.zeros(shape=(3,5), dtype=float)

entre muchas otras para gráficas, manejo de datos, ecuaciones algebraicas, sonido, etc.

---

Bloque de Ingreso en Python

Sección donde se pide o ingresa los datos necesarios para resolver el problema, es decir se obtienen los valores de las variables, etc.

Ejemplo: Pedir un número entero por teclado

a = int(input('pregunta: '))

Ejemplo: ingresar un número real por teclado

a = float(input('pregunta: '))

Ejemplo: ingresar un texto o palabra por teclado

a = input('pregunta: ')

---

Bloque de Procedimiento en Python

Donde se resuelve el problema con los datos ingresados. Aquí es donde más se usan las estructuras de control de operaciones, se desarrolla por bloques.

En cada bloque, la sangría o "indentación" indica dependencia del bloque.

Condicionales

Permite seleccionar una operación como resultado de una condición establecida.

if (Condicion):
    Verdadero
else:
    Falso

Ejemplo en Python:

if (a>b):
    a = a+3
else:
    b = b-2

Lazo o bucle: Mientras Repita

permite repetir un bloque de operaciones controlado por una condición.

while (condicion):
    operaciones

Ejemplo en Python:

a=50
while (a<100):
    a = a+5

Lazo o Bucle: Repita-Hasta

Se interpreta como: ejecutar "hasta" que se cumpla la condición.

while not(condicion):
    operaciones

Ejemplo en Python:

a=50
while not(a<100):
    a = a+5

---

Bloque de Salida en Python

Presenta los resultados encontrados al desarrollar la solución al problema.

Ejemplo: para mostrar una variable o un mensaje

print('Resultado: ')
print(variable)
print('mensaje:', respuesta)

En las siguiente secciones se dan más detalles, junto al desarrollo de los ejercicios.

[ Estructuras de control ] [ Condicional ] [ Bucle while ] [ Bucle for ]

---

Comentarios, preguntas o consultas:

@EdisonDelRosario,  edelrosespol,  @edelrosespol

3.1 Estructuras de Control en programación

3.2 Condicionales "if-else" - Estructura de selección

3.2.1 Condicionales "if-else" múltiple o con varios casos

3.2.2 Condicionales "if-else"- Ejercicios resueltos

3.2.3 Condicionales "if-else" - Ejercicios para Tarea

3.3 Bucles o Ciclos "while" - Estructuras para Repetir o iterar

3.3.1 Bucles o Ciclos - Ejercicios resueltos con Python

3.3.2 Bucles o Ciclos - Ejercicios y Tarea

3.4 Números Aleatorios, al Azar o random con Python

3.4.1 Números Aleatorios - Ejercicios resueltos en Python

3.5 Bases Numéricas en programación - Introducción

3.5.1 Número Binario a Decimal - Algoritmo Básico en Python

3.5.2 Número Decimal a Binario - Algoritmo Básico en Python

3.5.3 Bases Numéricas en programación - Ejercicios resueltos y Tarea