acumuladores y contadores – Página 4 – Fundamentos de Programación

2014-03-052023-02-04

1Eva_IIT2005_T4 Juego escaleras y serpientes

Parcial II Término 2005 – 2006. Diciembre 06, 2005 /ICM00794

Tema 4. (25 puntos).Para una nueva versión del juego “Escaleras y Serpientes” se desea disponer del algoritmo para simulación en computador.

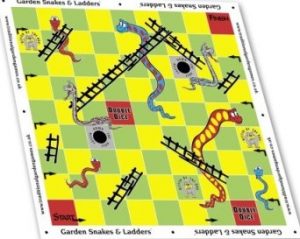
escaleraserpiente

El juego para dos jugadores consiste en llegar a la meta en primer lugar en un tablero de 64 casillas cuyas especificaciones son las siguientes:

Al inicio los jugadores están en una misma posición y arrancan su trayectoria cuando lanzando una moneda (cara 1 o 2) el jugador que gane empieza.
Cada jugador realiza su recorrido alternadamente de acuerdo a los resultados de los lanzamientos de un dado (6 caras)
Al avanzar, el jugador puede “caer” en una “casilla de castigo”, por lo que retrocederá 3 pasos de la posición en la que se encuentra. Si cae en “casilla de premio”, el usuario avanzará 3 pasos de la posición en la que se encuentra.
Luego de un lanzamiento y determinación de la posición final, el jugador le pasa el turno al otro jugador.
Se repite el juego desde el paso 2 hasta que uno de los jugadores pase la meta.

Al final se deberá mostrar:
– Número de veces jugadas por cada jugador, y
– El jugador que ganó.

Nota: casillas de premio para éste tema son: 4, 9, 29, 34, 46 y de castigo: 8, 19, 38, 50, 60

2014-03-052023-02-04

1Eva_IT2005_T3 Arreglo aleatorio binario a decimal

Parcial I Término 2005 – 2006. Julio 05, 2005 /ICM00794

Tema 3. (30 puntos). Suponga un vector B[i] de n componentes enteros.
Diseñe un algoritmo estructurado que almacene en cada celda un número aleatorio binario de una cifra (1 ó 0).

a) Determine si la cantidad de 1’s es par o impar
b) Calcule el equivalente numérico decimal del número binario almacenado.
c) Muestre los resultados de los literales a) y b).

*Ejemplo*: Vector B[i] con n=8
i	B[i]	Equivalente decimal:
1	1	1*2⁷+
2	1	1*2⁶+
3	0	0*2⁵+
4	1	1*2⁴+
5	0	0*2³+
6	0	0*2²+
7	1	1*2¹+
8	0	0*2⁰
	Total de 1’s es Par	=210₁₀

2014-03-052023-02-04

1Eva_IIT2005_T2 Negocio piramidal

Parcial II Término 2005 – 2006. Diciembre 06, 2005 /ICM00794

Tema 2. (25 puntos).

Considere el desarrollo del siguiente negocio:

a. Una persona entrega x dólares, y se le paga 10% mensual del valor inicial depositado en forma permanente.

b. Suponga que las personas NO retiran el dinero depositado, solo los intereses que se generan

c. La persona que recibe el dinero de los participantes usa el 20% del dinero x depositado de cada persona como comisión por gestión y gastos, quedando como saldo lo que había menos intereses y menos comisiones.

d. Suponga que cada mes se duplica la cantidad de personas que invierte la misma cantidad x de dinero, con las mismas condiciones.

e. Pero únicamente hay n personas que pueden entrar al negocio.

Describa un algoritmo para determinar en cuál mes no habrá suficiente dinero para pagar a los depositantes.

Referencia: Estafas piramidales son repetitivas en Sudamérica y el mundo. eluniverso.com 2008/11/30. https://www.eluniverso.com/2008/11/30/0001/12/636B87E403CB41EE9A5A7FF5DAF79978.html

2014-03-052023-02-04

1Eva_IT2005_T2 Valor de π por multiplicadores

Parcial I Término 2005 – 2006. Julio 05, 2005 /ICM00794

Tema 2. (30 puntos). El número π puede ser obtenido mediante la siguiente aproximación con un número n grande:

Realice un algoritmo para encontrar el valor aproximado de π con la fórmula mostrada para n dado.

2014-03-042023-02-04

1Eva_IIT2004_T2 Apuestas a números con dados

Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

Tema 2. (25 puntos) Simule en un algoritmo el juego descrito entre dos personas: A y B.
Muestre cuál jugador gana el juego y cuántos turnos se tuvieron que jugar.

Inicialmente cada una tiene $20
En cada turno se lanza un dado
Si sale 6 o 4, A gana $3 y B pierde $3
Si sale 2, ninguno gana ni pierde
Si sale 1, A pierde $6 y B gana $6
Si sale 3 o 5, A pierde $1 y B gana $1

El juego termina cuando una de las dos personas pierde todo su dinero.

2014-03-042023-02-04

1Eva_IIT2004_T1 Nicómano de Gerasa

Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

Para cada tema describa un algoritmo con un Diagrama de Flujo, Seudolenguaje , o Matlab

Tema 1. (25 puntos) Nicómano de Gerasa descubrió la siguiente propiedad de los números naturales:

Al sumar el primer impar se obtiene el primer cubo:	1 = 1
Al sumar los dos siguientes impares se obtiene el segundo cubo:	3+5 = 8
Al sumar los tres siguientes impares se obtiene el tercer cubo:	7+9+11 = 27
Al sumar los cuatro siguientes impares se obtiene el cuarto cubo:	13+15+17+19 = 64 Etc…

Con esta propiedad, para un n dado, calcule y muestre los cubos de los primeros n números naturales.

2014-03-042023-02-04

1Eva_IT2004_T2 Verificar ISBN

Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

Tema 2. (25 puntos) El número estándar internacional de un libro (ISBN: International Standard Book Number) es un código de 10 dígitos. La última cifra es un dígito verificador que indica si el ISBN está correcto.

El dígito verificador es obtenido mediante la operación residuo de S para 11, donde S es la suma de:

una vez el primer dígito,
mas dos veces el segundo dígito,
mas tres veces el tercer dígito,
. . . ,
mas nueve veces el noveno dígito.

Ejemplo:
 la suma S para el ISBN 9684443242 es:
 1*9+2*6+3*8+4*4+5*4+6*4+7*3+8*2+9*4 = 178
 El dígito verificador es el residuo(178/11) 
 que es igual a 2.

a) Escriba un algoritmo que lea un número ISBN que verifique si éste es o no correcto.

b) Realice la prueba de escritorio de su algoritmo, utilizando el ISBN 9701702533.

Referencia: ¿Qué es un ISBN? isbn-international.org. https://www.isbn-international.org/es/content/%C2%BFqu%C3%A9-es-un-isbn

2014-03-042023-02-04

1Eva_IT2004_T1 Aleatorios en región sombreada

Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

Tema 1. (25 puntos) Escriba un algoritmo que genere aleatoriamente 1000 pares ordenados (x,y), donde x e y son números reales con 2 cifras decimales, tales que: franjaplano

0.00 ≤ x ≤ 4.00

0.00 ≤ y ≤ 4.00

Su algoritmo deberá determinar la cantidad de puntos que se ubicaron dentro de la región sombreada mostrada en la figura.

Rúbrica: Generar n pares aleatorios (5 puntos), verificar punto debajo de frontera superior (5 puntos), verificar punto por encima de frontera inferior (5 puntos). Conteo de puntos en franja (5 puntos). Algoritmo estructurado (5 puntos)

2014-03-032023-02-04

1Eva_IIIT2003_T3 Coordenadas enteras en un círculo

Parcial III Término 2003 – 2004. Abril 02, 2004 /ICM00794

Tema 3. (25 puntos) Escriba un algoritmo en seudo-código para determinar el número de puntos del plano cartesiano con coordenadas de valores enteros que pertenecen al círculo limitado por la circunferencia de ecuación

x^2 + y^2 = 100

(centro en el origen y radio 10).

Muestre también el promedio de las distancias de dichos puntos al origen de coordenadas.

Rúbrica: Manejo de índices enteros como coordenadas (5 puntos). control de intervalos de coordendas en dos dimensiones (5 puntos), manejo de contadores y condicionales (10 puntos), promedio de distancias (5 puntos).

2014-03-032023-02-04

1Eva_IIIT2003_T2 Verificar números triangulares

Parcial III Término 2003 – 2004. Abril 02, 2004 /ICM00794

Tema 2. (25 puntos) Considere la secuencia de números triangulares, cuyo nombre refleja su ley de formación:

1, 3, 6, 10, …

Escriba un algoritmo en seudo-código que indique si un número natural t, ingresado por teclado, es triangular.

Esto es, si es de la forma:

t = \sum_{i=1}^{n}i

para algún número natural n

Rúbrica: identificación de piso en operación (5 puntos), cálculo de usados (5 puntos), control de pisos construidos (5 puntos), validar s es triangular (5 puntos), algoritmo estructurado (5 puntos)

Referencia: Número triangular. Wikipedia