Publicado en

1Eva_IT2012_T1 Codificar número por dígito

1ra Evaluación I Término 2012-2013. Julio 03, 2012 /ICM00794

TEMA 1 (20 puntos) Para cierta aplicación informática se necesitan codificar números enteros.

Elabore un ALGORITMO que solicite al usuario un número entero positivo de tres dígitos, el cual necesita ser codificado.

Considere que:
a) Si el dígito de dicho número es 2, 5 o 7, se le debe sumar la unidad.
b) Si el dígito es 1, 4, 8 o 9, se le resta la unidad.
c) Los dígitos restantes no se alteran.

Ejemplos:

Original Codificado
472 ← 383
503 ← 603
615 ← 606

Rúbrica: Validación (5 puntos), conversión por dígito (10 puntos), número codificado(5 puntos)

Publicado en

1Eva_IIT2011_T2 Número de serie, reclamo por daño

1ra Evaluación II Término 2011-2012. Noviembre 29, 2011 /ICM00794

Tema 2. (20 puntos) El número de serie de un producto de 12 dígitos está compuesto por: dos dígitos del año, dos dígitos del mes, dos dígitos del día, dos del inspector de calidad y cuatro del su orden en la producción del día. numero de serie producto

Cuando un producto retorna por defectos de fábrica, se asigna la revisión al inspector de calidad responsable del producto indicando la fecha de fabricación.

Realice un algoritmo para atender un reclamo por defecto de fábrica, que permita ingresar un número de serie, revise si dispone de 12 dígitos, extraiga la información del producto el inspector responsable y la fecha del reporte de producción.

Nota: No se consideran años de producción previos al año 2010.

Rúbrica: Ingreso y validación (5 puntos), extracción de información (10 puntos), mostrar resultados (5 puntos).

Publicado en

1Eva_IT2010_T2 Número Omirp

1ra Evaluación I Término 2010-2011. Julio 6, 2010 /ICM00794

Tema 2. (25 puntos) Omirp se define como,
un número primo que al invertir sus dígitos da otro número primo.

Escriba un algoritmo para determinar si un número n tiene la característica de ser un número Omirp.

Ejemplo:

 1597 es número primo,
 Se invierte sus dígitos: 7951
 7951 es primo,
 Entonces el número 1597 es un número omirp.

Rúbrica: Validar si n es primo (7 puntos), invertir los dígitos del número (10 puntos), validar si el nuevo número es primo (3 puntos), respuesta y algoritmo integrado (5 puntos)

Publicado en

1Eva_IT2008_T1 Teorema de Wilson

1ra Evaluación I Término 2008 – 2009. Julio 08, 2008 /ICM00794

Tema 1 (20 puntos). El teorema de Wilson enuncia que:

“Un número p es primo si y solo si el factorial (p-1)! + 1 es divisible por p”.

Escriba un algoritmo que solicite al usuario un número entero positivo p, determine si es primo, en el caso de serlo verifique que se cumple el teorema de Wilson.

Publicado en

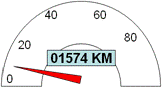1Eva_IIT2008_T1 Odómetro OCTAL

1ra Evaluación II Término 2008 – 2009. Diciembre 09, 2008 /ICM00794

Tema 1 (20 puntos). En un odómetro mecánico de un vehículo antiguo se marcan las distancias recorridas en kilómetros, en formato numérico octal de hasta cinco dígitos.

odometroRealice un algoritmo para encontrar la distancia recorrida en kilómetros en formato numérico decimal, convirtiendo el valor octal marcado por el odómetro luego de un viaje.

Nota: Un odómetro es un dispositivo que indica la distancia recorrida en un viaje de un vehículo.

Publicado en

1Eva_IIT2006_T2 Dígito verificador de cuenta

1ra Evaluación II Término 2006 – 2007. Diciembre 05, 2006 /ICM00794

Tema 2. (25 puntos) Cierta compañía tiene codificadas las cuentas de sus clientes y requiere que le proporcione un algoritmo que dado un código de cuenta, informe si es válido de acuerdo a la siguiente descripción: tecladocajero

  • Los códigos se conforman de 4 dígitos de la cuenta, contados de derecha a izquierda, más el dígito verificador.
  • El dígito verificador se obtiene:
    – sumando los dígitos del número de cuenta de las posiciones pares y
    – multiplicando los dígitos de las posiciones impares,
    – del nuevo resultado se extrae el residuo de la división para 10, el cual representa el dígito verificador calculado.
  • Si el verificador escrito es igual al verificador calculado, entonces el código de cuenta es válido
Ejemplo
Código: 25431
verificador escrito: 1
número de cuenta: 2543
Posiciones Pares: (4+2) =  6
Posiciones Impares: (3*5) = 15
Suma total:         21
residuo de 10 residuo(21/10) = 1
¿verificador calculado
y escrito iguales?		 el código es válido
Publicado en

2Eva_IIT2002_T3 Encriptar PIN(4 dígitos)

Final II Término 2002 – 2003. Febrero 13, 2002 /ICM00794

Tema 3. (20 puntos) Una compañía de telecomunicaciones tiene sospechas de que sus datos están siendo interceptados y desea transmitirlos de manera segura usando algoritmos de encriptación de tal forma que solo la pueda entender el destinatario. encriptar candado imagen

Toda su información se transmite como enteros de 4 dígitos.

El asesor de seguridad informática le recomienda seguir los siguientes pasos:

  • A cada dígito súmele siete.
  • Al resultado de esta suma, divídelo para 10 y extráigale el residuo.
  • El valor resultante reemplaza al dígito original
  • Intercambie el primer dígito con el tercero y el segundo con el cuarto.
Ejemplo: 
 >> encripta(1254)
 ans= 2189

a) Escriba una función encripta() que reciba numero entero de 4 dígitos (entre 1000 y 9999) y que retorne el mismo numero entero encriptado correspondientemente

b) Escriba un Programa que pida al usuario una clave de acceso (entero de 4 dígitos), verifique que sea válida en rango). Encripte la clave de acceso y la muestre en pantalla.

Publicado en

1Eva_IT2001_T5 Verificar divisibilidad para 9

Parcial II Término 2001 – 2002. Diciembre 11, 2001 /ICM00794

Tema 5. (20 puntos) «Un entero es divisible para 9 si lo es la suma de sus cifras.»

Escriba un diagrama de flujo que lea un numero N y sume sus cifras, si el resultado es mayor que 9 nuevamente sume sus cifras hasta obtener un número de un solo dígito.

Si este es el número 9 muestre el mensaje » EL NUMERO N ES DIVISIBLE PARA 9″.

Ejemplo:
N = 15478
    1+5+4+7+8 = 25
    2+5 = 7 
En este ejemplo el numero N no es divisible para 9

propuesta: m_pdf, py_pdf, sol_py