Publicado en

2Eva_IIT2018_T1 Masa entra o sale de un reactor

2da Evaluación II Término 2018-2019. 29/Enero/2019. MATG1013

Tema 1. (30 puntos) La integración proporciona un medio para calcular cuánta masa entra o sale de un reactor químico durante un periodo específico de tiempo. https://es.wikipedia.org/wiki/Reactor_qu%C3%ADmico

M = \int^{t_2}_{t_1}Q(t)C(t) dt

t : min
C(t) : mg/m3
Q(t) : m3/min

a) Con los datos mostrados en la tabla y usando los métodos de Simpson 1/3 y 3/8, aproxime la cantidad de masa que sale de un reactor entre t1=0 y t2=25 min.

t 0 5 10 15 20 25
C(t) 10 18 27 35 40 30
Q(t) 4 6 7 6 5 5

b) Estime el error

Rúbrica: Conoce los métodos de Simpson hasta (5 puntos), Calcula la función a integrar hasta (5 puntos), Separa los intervalos hasta (5 puntos), Aplica las fórmulas correctamente hasta (5 puntos). Literal b, conoce las fórmulas del error (5 puntos), calcula los errores (5 puntos)

Referencia: Chapra problema 24.4 p693 pdf717. Reactor químico, https://es.wikipedia.org/wiki/Reactor_qu%C3%ADmico

t = [0,5,10,15,20,25]
C = [10,18,27,35,40,30]
Q = [4,6,7,6,5,5]
Publicado en

2Eva_IT2018_T4 Dragado acceso marítimo

2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013

Tema 4. (30 puntos) Para una sección de 500 m del acceso marítimo a los puertos de Guayaquil se requiere de un canal con:

  • profundidad mínima de 11 metros MLWS
  • ancho de 250 m

de tal foma que permita navegar buques de carga de mayor tamaño.

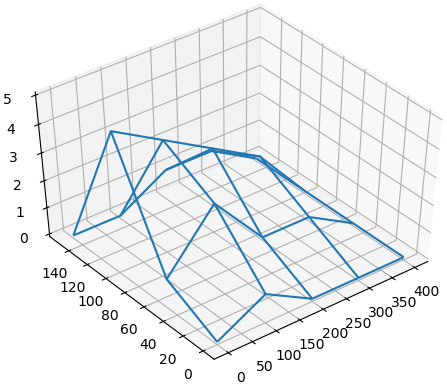
Dispone de las mediciones de profundidad mostradas en la tabla de batimetría:

Batimetría
yi \ xi 0 50 100 150 200 250
0 -6.79 -12.03 -10.04 -11.60 -7.24 -7.91
100 -8.85 -10.89 -8.95 -7.23 -11.42 -7.93
200 -11.90 -9.86 -9.35 -12.05 -9.38 -9.65
300 -7.30 -11.55 -10.41 -8.67 -11.84 -6.77
400 -12.17 -9.62 -7.47 -6.51 -9.02 -9.60
500 -11.90 -10.23 -10.68 -9.94 -6.76 -7.46

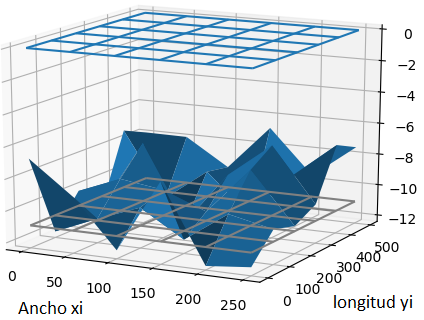
a) Obtenga la tabla de dragado como la diferencia entre la profundidad del canal requerido y la tabla de batimetría.

b) Estime el volumen de sedimentos a remover por la draga usando integración por el método de Simpson.

Nota: Si el fondo está más alla de los 11 metros, no se requiere la intervención de la draga.

Rúbrica: literal a (5 puntos), selección apropiada del método por rango, aplicación en un eje (15 puntos), integración en el otro eje (5 puntos), presentar las iteraciones correctamente (5 puntos)

MLWS: Nivel Medio de las Bajamares de Sicigia / nivel de referencia.
Batimetría: es el levantamiento del relieve de Superficies Subacuáticas

Referencias: El dragado del canal a los puertos de Guayaquil se anunciará el 26 de marzo del 2018. El comercio. 21/03/2018. https://www.elcomercio.com/actualidad/dragado-canal-puertos-guayaquil-jaimenebot.html.
Calado de puertos. El universo. 2013.08.16 https://www.eluniverso.com/noticias/2013/08/16/nota/1294716/calado-puertos-region-llega-138-m,
Operación Draga: https://www.youtube.com/watch?v=goDq5Ypk–c

profcanal = 11

xi = np.array([ 0.,  50., 100., 150., 200., 250.])
yi = np.array([ 0., 100., 200., 300., 400., 500.])

batimetria = [[ -6.79,-12.03,-10.04,-11.60, -7.24,-7.91],
              [ -8.85,-10.89, -8.95, -7.23,-11.42,-7.93],
              [-11.90, -9.86, -9.35,-12.05, -9.38,-9.65],
              [ -7.30,-11.55,-10.41, -8.67,-11.84,-6.77],
              [-12.17, -9.62, -7.47, -6.51, -9.02,-9.60],
              [-11.90,-10.23,-10.68, -9.94, -6.76,-7.46]]

batimetria = np.array(batimetria)
Publicado en

2Eva_IT2018_T3 EDP Eliptica

2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013

Tema 3. (25 puntos) Considere el problema con valores en la frontera:

\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = 2(x^2+y^2) 0<x<1 0<y<1

con las condiciones de frontera en los mismos intervalos que la ecuacion diferencial:

u(x,0) = x + 1 u(0,y) = y+1 u(x,1) = x^2 + x +2 u(1,y) = y^2 + y +2

Use el método de diferencias finitas para resolver el problema tomando como tamaño de paso hx = hy = 1/3

Rúbrica: Selección de diferencias finitas divididas, gráfica del problema (5 puntos), ecuación generalizada con diferencias finitas divididas (5 puntos), Sistema de ecuaciones para los puntos desconocidos (10 puntos). Valores de los puntos desconocidos (5 puntos)

 

Publicado en

2Eva_IT2018_T2 Deducir Simpson 1/3

2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013

Tema 2. (20 puntos) Deduzca el método de Simpson 1/3

Sugerencias: Una de las formas de plantear la deducción es usando un polinomio de Lagrange con grado 2 para aproximar la función que pasa por los puntos [a,f(a)], [b,f(b)] y [c,f(c)].

Considere que los tramos tienen h tienen tamaño (b-a)/2, (c-a), (b-c)

Plantee la ecuación y sustituya los valores de los tramos por valores de h para resolver todo en función de h.

Rúbrica: Planteo del problema con polinomio (5 puntos), desarrollo del problema con integral (5 puntos c/u).

Publicado en

2Eva_IT2018_T1 Paracaidista wingsuit

2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013

Tema 1. (25 puntos) Si suponemos que el arrastre es proporcional al cuadrado de la velocidad, se puede modelar la velocidad de un objeto que cae, como un paracaidista, por medio de la ecuación diferencial ordinaria:

\frac{dv}{dt} = g - \frac{cd}{m} v^2

Donde:  http://www.elperiodicodearagon.com/noticias/sociedad/alarma-francia-cinco-muertes-verano-moda-hombres-pajaro-wingsuit_877164.html

  • v es la velocidad en m/s
  • cd es el coeficiente de arrastre de segundo orden Kg/m
  • m es la masa en Kg
  • v = \frac{dy}{dt}
  • y es la distancia que recorre en m

Resuelva para la velocidad y distancia que recorre un objeto de 90 Kg con coeficiente de arrastre de 0.225 kg/m.

Si la velocidad inicial es 0 y la altura inicial es 1 Km, determine la velocidad y posición en cada tiempo, usando un tamano de paso de 2s.

a) Plantee la solución de las ecuaciones para la velocidad y distancia usando el método de Runge-Kutta de segundo orden

b) Realice tres iteraciones

Rúbrica: literal a (15 puntos), literal b (10 puntos)

Referencia: Alarma en Francia … por moda wingsuit. 23 Agosto 2013. www.elperiodicodearagon.com.  http://www.elperiodicodearagon.com/noticias/sociedad/alarma-francia-cinco-muertes-verano-moda-hombres-pajaro-wingsuit_877164.html

Publicado en

2Eva_IIT2017_T4 EDO valor en frontera

2da Evaluación II Término 2017-2018. Febrero 7, 2018. MATG1013

Tema 4. Use el algoritmo lineal de diferencias finitas para aproximar la solución del problema con valor en las fronteras

\frac{d^2T}{dx^2} + \frac{1}{x}\frac{dT}{dx} +S =0 0 \leq x \leq 1

con condiciones de frontera

T(x=0) =2, T(x=1) = 1

a) Plantee las ecuaciones con h = 0.25

b) Plantee el error para Ti

c) Realice los cálculos con S=1

Publicado en

2Eva_IIT2017_T3 EDP parabólica con diferencias regresivas

2da Evaluación II Término 2017-2018. Febrero 7, 2018. MATG1013

Tema 3. Aproxime la solución de la sigiente EDP parcial usando diferencias regresivas

\frac{\partial U}{ \partial t} - \frac{1}{16} \frac{\partial ^2U}{\partial x^2} = 0 0 \lt x \lt 1 , 0\lt t U(0,t) = U(1,t) = 0, 0\lt t, U(x,0) = 2 \sin (\pi x), 0\leq x \leq 1

a) Plantee las ecuaciones usando hx = 1/3, ht = 0.05, T = 2

b) Calcule U(xi,tj)

c) Plantee el error de U(xi,tj)

Publicado en

2Eva_IIT2017_T2 Volumen de isla

2da Evaluación II Término 2017-2018. Febrero 7, 2018. MATG1013

Tema 2. Se tienen las coordenadas (x,y) y las alturas f(x,y) de una isla sobre el nivel del mar obtenidas por internet como se ilustra en la tabla.

El nodo que está en el agua tiene altura cero.

x0 = 0 x1 = 100 x2 = 200 x3 = 300 x4 = 400
 y0 = 0 0 1 0 0 0
y1 = 50 1 3 1 1 0
y2 = 100  5  4 3 2 0
y3 = 150 0 0 1 1 0

Las unidades de los ejes se encuentran en metros.

a) Plantee el volumen de la isla como una integral doble en una región rectangular,

b) Usando los métodos de Simpson, plantee la formulación para aproximar el volumen,

c) Aproxime el volumen de la isla

d) Estime el error

isla = [[0,1,0,0,0],
        [1,3,1,1,0],
        [5,4,3,2,0],
        [0,0,1,1,0]]

xi = [0,100,200,300,400]
yi = [0, 50,100,150])
Publicado en

2Eva_IIT2017_T1 EDO Runge Kutta 2do Orden d2y/dx2

2da Evaluación II Término 2017-2018. Febrero 7, 2018. MATG1013

Tema 1. Use el método de Runge Kutta de 2do orden (Euler Mejorado) para sistemas de ecuaciones y aproxime la solución de la EDO de orden superior

\frac{d^2\theta}{dt^2} + \frac{g}{L}\sin (\theta) = 0 \theta (0) = \frac{\pi}{6}, \theta '(0) =0

Suponga que g=9.8 y L=2

a) Plantee la formulación para 0 ≤t≤2, h=0.1

b) Calcule el ángulo para t=1, usando h=0.25

c) Estime el error (solo la fórmula del error para Euler Mejorado)

Publicado en

2Eva_IT2017_T3 EDP parabólica

2da Evaluación I Término 2017-2018. 28/Agosto/2017. MATG1013

Tema 3. (30 puntos) Use el método de diferencias progresivas para aproximar la solución de la siguiente ecuación diferencial parcial parabólica:

\frac{\partial u}{\partial t} - \frac{1}{\pi ^2} \frac{\partial ^2 u}{\partial x^2} =0

0 ≤ x ≤ 1, t>0

condiciones de borde: u(0,t) = u(1,t) = 0, t>0,
condiciones iniciales u(x,0) = cos(π(x-0.5)), 0 ≤ x ≤ 1

a) Use dx = 0.2 y dt = 0.01. Realize 3 pasos en el tiempo.

b) Estime el error.

c) Calcule la temperatura promedio para t=0 como el área bajo la curva, mediante el método de Simpson. Repita para t=0.01 y calcule el porcentaje que disminuye.

Rúbrica: Construir la malla hasta 5 puntos, plantear la ecuación en el nodo i,j hasta 5 puntos, calcular el estimado de u(i,j) hasta la tercera fila hasta 5 puntos, calcular la temperatura media estimada hasta 5 puntos.