Unidades – Página 7 – Métodos numéricos

Métodos Directos

Gauss

Gauss-Jordan

Métodos Iterativos

Jacobi

Gauss-Seidel

2017-09-022024-10-03

2.7 Métodos de raíces con gráficos animados en Python

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]

Solo para fines didácticos, y como complemento para los ejercicios presentados en la unidad para raíces de ecuaciones, se presentan las instrucciones para las animaciones usadas en la presentación de los conceptos y ejercicios. Los algoritmos para animación NO son necesarios para realizar los ejercicios, que requieren una parte analítica con al menos tres iteraciones en papel y lápiz. Se lo adjunta como una herramienta didáctica de asistencia para las clases.

La gráfica (graf_ani) se crea en una ventana (fig_ani), inicializando con la linea a partir f(x) y configurando los parámetros base para el gráfico.

Se usan procedimientos para crear unatrama() para marca de iteración y en cada cambio se limpia la trama manteniendo la base con limpiatrama().

En caso de requerir un archivo .gif animado se proporciona un nombre de archivo. Para crear el archivo se requiere de un complemento ‘imagemagick‘ a ser instalado.

otros ejemplos de animación en el curso de Fundamentos de Programación:

Movimiento circular – Una partícula, animación con matplotlib-Python

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
..

Método de la Bisección con gráfico animado en Python

# Algoritmo de Bisección, Tabla
# Los valores de [a,b] son aceptables
# y seleccionados desde la gráfica de la función
# error = tolera

import numpy as np

def biseccion_tabla(fx,a,b,tolera,iteramax = 20,
                    vertabla=False, precision=6):
    '''Algoritmo de Bisección
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    error = tolera
    '''
    fa = fx(a)
    fb = fx(b)
    tramo = np.abs(b-a)
    itera = 0
    cambia = np.sign(fa)*np.sign(fb)
    tabla=[]
    if cambia<0: # existe cambio de signo f(a) vs f(b)
        if vertabla==True:
            print('método de Bisección')
            print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
            print('  ','tramo')
            np.set_printoptions(precision)
            
        while (tramo>=tolera and itera<=iteramax):
            c = (a+b)/2
            fc = fx(c)
            cambia = np.sign(fa)*np.sign(fc)
            unafila = [a,c,b,fa,fc,fb] 
            if vertabla==True:
                print(itera,[a,c,b],np.array([fa,fc,fb]))
            if (cambia<0):
                b = c
                fb = fc
            else:
                a = c
                fa = fc
            tramo = np.abs(b-a)
            unafila.append(tramo)
            tabla.append(unafila)
            if vertabla==True:
                print('  ',tramo)
            itera = itera + 1
        respuesta = c
        # Valida respuesta
        if (itera>=iteramax):
            respuesta = np.nan

    else: 
        print(' No existe cambio de signo entre f(a) y f(b)')
        print(' f(a) =',fa,',  f(b) =',fb) 
        respuesta=np.nan
    tabla = np.array(tabla,dtype=float)
    return(respuesta,tabla)

# PROGRAMA #######################

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10

a = 1
b = 2
tolera = 0.001

# PROCEDIMIENTO
[raiz,tabla] = biseccion_tabla(fx,a,b,tolera,vertabla=True)

# SALIDA
print('raíz en: ', raiz)

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
xc = tabla[:,1]
yc = tabla[:,4]

plt.plot(xi,fi, label='f(x)')
plt.plot([a,b],[fx(a),fx(b)],'o',
         color='red',label='[[a,b],[f(a),f(b)]]')
plt.scatter(xc,yc,color='orange', label='[c,f(c)]')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Bisección')
plt.grid()
plt.legend()
#plt.show()

# GRAFICA CON ANIMACION ------------
import matplotlib.animation as animation

xa = tabla[:,0]
ya = tabla[:,3]
xb = tabla[:,2]
yb = tabla[:,5]
xc = tabla[:,1]
yc = tabla[:,4]

# Inicializa parametros de trama/foto
narchivo = 'Biseccion' # nombre archivo
retardo = 700 # milisegundos entre tramas
tramas = len(xa)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
ymax = np.max(fi)
ymin = np.min(fi)
deltax = np.abs(b-a)
deltay = np.abs(ymax-ymin)
graf_ani.set_xlim([a-0.05*deltax,b+0.05*deltax])
graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.05*deltay])
# Lineas y puntos base
lineafx,= graf_ani.plot(xi,fi, label='f(x)')

puntoa, = graf_ani.plot(xa[0], ya[0],'o',
                        color='red', label='a')
puntob, = graf_ani.plot(xb[0], yb[0],'o',
                        color='green', label='b')
puntoc, = graf_ani.plot(xc[0], yc[0],'o',
                        color='orange', label='c')
lineaa, = graf_ani.plot([xa[0],xa[0]],
                        [0,ya[0]],color='red',
                        linestyle='dashed')
lineab, = graf_ani.plot([xb[0],xb[0]],
                        [0,yb[0]],color='green',
                        linestyle='dashed')
lineac, = graf_ani.plot([xc[0],xc[0]],
                        [0,yc[0]],
                        color='orange',
                        linestyle='dashed')
# Configura gráfica
linea0 = graf_ani.axhline(0, color='k')
graf_ani.set_title('Bisección')
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Cada nueva trama
def unatrama(i,xa,ya,xb,yb,xc,yc):
    # actualiza cada punto
    puntoa.set_xdata(xa[i]) 
    puntoa.set_ydata(ya[i])
    puntob.set_xdata(xb[i])
    puntob.set_ydata(yb[i])
    puntoc.set_xdata(xc[i])
    puntoc.set_ydata(yc[i])
    # actualiza cada linea
    lineaa.set_ydata([ya[i], 0])
    lineaa.set_xdata([xa[i], xa[i]])
    lineab.set_ydata([yb[i], 0])
    lineab.set_xdata([xb[i], xb[i]])
    lineac.set_ydata([yc[i], 0])
    lineac.set_xdata([xc[i], xc[i]])
    return (puntoa, puntob, puntoc, lineaa, lineab, lineac,)

# Limpia trama anterior
def limpiatrama():
    puntoa.set_ydata(np.ma.array(xa, mask=True))
    puntob.set_ydata(np.ma.array(xb, mask=True))
    puntoc.set_ydata(np.ma.array(xc, mask=True))
    lineaa.set_ydata(np.ma.array([0,0], mask=True))
    lineab.set_ydata(np.ma.array([0,0], mask=True))
    lineac.set_ydata(np.ma.array([0,0], mask=True))
    return (puntoa, puntob, puntoc, lineaa, lineab, lineac,)

# contador de tramas
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(fig_ani,unatrama,
                              i ,
                              fargs=(xa, ya,
                                     xb, yb,
                                     xc, yc),
                              init_func=limpiatrama,
                              interval=retardo,
                              blit=True)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_animado.gif', writer='imagemagick')
#ani.save(narchivo+'_animado.mp4')
plt.show()

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]

Método de la Posición Falsa con gráfico animado en Python

# Algoritmo de falsa posicion para raices
# Los valores de [a,b] son seleccionados
# desde la gráfica de la función
# error = tolera

import numpy as np

def posicionfalsa_tabla(fx,a,b,tolera,iteramax = 20,
                        vertabla=False, precision=6):
    '''fx en forma numérica lambda
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    error = tolera
    '''
    fa = fx(a)
    fb = fx(b)
    tramo = np.abs(b-a)
    itera = 0
    cambia = np.sign(fa)*np.sign(fb)
    tabla = []
    if cambia<0: # existe cambio de signo f(a) vs f(b)
        if vertabla==True:
            print('método de la Posición Falsa ')
            print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
            print('  ','tramo')
            np.set_printoptions(precision)

        while (tramo >= tolera and itera<=iteramax):
            c = b - fb*(a-b)/(fa-fb)
            fc = fx(c)
            cambia = np.sign(fa)*np.sign(fc)
            unafila = [a,c,b,fa, fc, fb]
            if vertabla==True:
                print(itera,np.array([a,c,b]),
                      np.array([fa,fc,fb]))
            if (cambia > 0):
                tramo = np.abs(c-a)
                a = c
                fa = fc
            else:
                tramo = np.abs(b-c)
                b = c
                fb = fc
            unafila.append(tramo)
            tabla.append(unafila)
            if vertabla==True:
                print('  ',tramo)
            itera = itera + 1
        respuesta = c
        # Valida respuesta
        if (itera>=iteramax):
            respuesta = np.nan
    else: 
        print(' No existe cambio de signo entre f(a) y f(b)')
        print(' f(a) =',fa,',  f(b) =',fb) 
        respuesta=np.nan
    tabla = np.array(tabla,dtype=float)
    return(respuesta,tabla)

# PROGRAMA ----------------------

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10

a = 1
b = 2
tolera = 0.001

# PROCEDIMIENTO
[raiz,tabla] = posicionfalsa_tabla(fx,a,b,tolera,
                                   vertabla=True)
# SALIDA
print('raíz en: ', raiz)

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
xc = tabla[:,1]
yc = tabla[:,4]

plt.plot(xi,fi, label='f(x)')
plt.plot([a,b],[fx(a),fx(b)],'o',
         color='red',label='[[a,b],[f(a),f(b)]]')
plt.scatter(xc,yc,color='orange', label='[c,f(c)]')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Posición Falsa')
plt.grid()
plt.legend()
#plt.show()

# GRAFICA CON ANIMACION ------------
#import matplotlib.pyplot as plt
import matplotlib.animation as animation

xa = tabla[:,0]
ya = tabla[:,3]
xc = tabla[:,1]
yc = tabla[:,4]
xb = tabla[:,2]
yb = tabla[:,5]

# Inicializa parametros de trama/foto
narchivo = 'PosicionFalsa' # nombre archivo
retardo = 700 # milisegundos entre tramas
tramas = len(xa)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
graf_ani.set_xlim([a,b])
graf_ani.set_ylim([np.min(fi),np.max(fi)])
# Lineas y puntos base
lineafx, = graf_ani.plot(xi,fi,label ='f(x)')

puntoa, = graf_ani.plot(xa[0], ya[0],'o',
                        color='red', label='a')
puntob, = graf_ani.plot(xb[0], yb[0],'o',
                        color='green', label='b')
puntoc, = graf_ani.plot(xc[0], yc[0],'o',
                        color='orange', label='c')

lineaab, = graf_ani.plot([xa[0],xb[0]],[ya[0],yb[0]],
                        color ='orange',
                        label='y=mx+b')
lineac0, = graf_ani.plot([xc[0],xc[0]],[0,yc[0]],
                        color='magenta',
                        linestyle='dashed')

# Configura gráfica
linea0 = graf_ani.axhline(0, color='k')
graf_ani.set_title('Posición Falsa')
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Cada nueva trama
def unatrama(i,xa,ya,xc,yc,xb,yb):
    # actualiza cada punto
    puntoa.set_xdata(xa[i])
    puntoa.set_ydata(ya[i])
    puntob.set_xdata(xb[i])
    puntob.set_ydata(yb[i])
    puntoc.set_xdata(xc[i])
    puntoc.set_ydata(yc[i])
    # actualiza cada linea
    lineaab.set_ydata([ya[i], yb[i]])
    lineaab.set_xdata([xa[i], xb[i]])
    lineac0.set_ydata([0, yc[i]])
    lineac0.set_xdata([xc[i], xc[i]])  
    return (puntoa, puntob, puntoc, lineaab,lineac0,)

# Cada nueva trama
def limpiatrama():
    puntoa.set_ydata(np.ma.array(xa, mask=True))
    puntob.set_ydata(np.ma.array(xb, mask=True))
    puntoc.set_ydata(np.ma.array(xc, mask=True))
    lineaab.set_ydata(np.ma.array([0,0], mask=True))
    lineac0.set_ydata(np.ma.array([0,0], mask=True))
    return (puntoa, puntob, puntoc, lineaab,lineac0,)

# contador de tramas
i = np.arange(0, tramas,1)
ani = animation.FuncAnimation(fig_ani,unatrama,
                              i ,
                              fargs=(xa, ya,
                                     xc, yc,
                                     xb,yb),
                              init_func=limpiatrama,
                              interval=retardo,
                              blit=True)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_animado.gif', writer='imagemagick')
#ani.save(narchivo+'.mp4')
plt.show()

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
..

Método de Newton-Raphson con gráfico animado en Python

# Método de Newton-Raphson
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)
import numpy as np

def newton_raphson_tabla(fx,dfx,xi, tolera, iteramax=100,
                   vertabla=False, precision=4):
    '''
    fx y dfx en forma numérica lambda
    xi es el punto inicial de búsqueda
    '''
    itera=0
    tramo = abs(2*tolera)
    tabla = []
    if vertabla==True:
        print('método de Newton-Raphson')
        print('i', ['xi','fi','dfi', 'xnuevo', 'tramo'])
        np.set_printoptions(precision)
    while (tramo>=tolera):
        fi = fx(xi)
        dfi = dfx(xi)
        xnuevo = xi - fi/dfi
        tramo = abs(xnuevo-xi)
        if vertabla==True:
            print(itera,np.array([xi,fi,dfi,xnuevo,tramo]))

        tabla.append([xi,fi,dfi,xnuevo,tramo])
        xi = xnuevo
        itera = itera + 1

    if itera>=iteramax:
        xi = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    tabla = np.array(tabla,dtype=float)
    return(xi,tabla)

# PROGRAMA ----------------------

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10
dfx = lambda x: 3*(x**2) + 8*x

a = 1
b = 4
x0 = 3
tolera = 0.001

# PROCEDIMIENTO
[raiz,tabla] = newton_raphson_tabla(fx, dfx, x0,
                             tolera, vertabla=True)
# SALIDA
print('raiz en :', raiz)

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
xc = tabla[:,3]
yc = fx(xc)

plt.plot(xi,fi, label='f(x)')
plt.plot(x0,fx(x0),'o',
         color='red',label='[x0,f(x0)]')
plt.scatter(xc,yc,color='orange', label='[c,f(c)]')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
#plt.show()

# GRAFICA CON ANIMACION ------------
#import matplotlib.pyplot as plt
import matplotlib.animation as animation

xa = tabla[:,0]
ya = tabla[:,1]
xb = tabla[:,3]
dfi = tabla[:,2]
# Aproximacion con tangente
b0 = ya[0] - dfi[0]*x0
tangentei = dfi[0]*xi + b0
ci = -b0/dfi[0]

# Inicializa parametros de trama/foto
narchivo = 'NewtonRaphson' # nombre archivo
retardo = 700 # milisegundos entre tramas
tramas = len(xa)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
graf_ani.set_xlim([a,b])
graf_ani.set_ylim([np.min(fi),np.max(fi)])
# Lineas y puntos base
lineafx, = graf_ani.plot(xi,fi,label ='f(x)')

puntoa, = graf_ani.plot(xa[0], ya[0],'o',
                        color='red', label='x[i]')
puntob, = graf_ani.plot(xb[0], 0,'o',
                        color='green', label='x[i+1]')

lineatanx, = graf_ani.plot(xi,tangentei,
                           color='orange',label='tangente')
lineaa, = graf_ani.plot([xa[0],xa[0]],
                        [ya[0],0], color='magenta',
                        linestyle='dashed')
lineab, = graf_ani.plot([xb[0],xb[0]],
                         [0,fx(xb[0])], color='magenta',
                         linestyle='dashed')
# Configura gráfica
linea0 = graf_ani.axhline(0, color='k')
graf_ani.set_title('Newton-Raphson')
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Cada nueva trama
def unatrama(i,xa,ya,xb,dfi):
    # actualiza cada punto
    puntoa.set_xdata(xa[i]) 
    puntoa.set_ydata(ya[i])
    puntob.set_xdata(xb[i])
    puntob.set_ydata(0)
    # actualiza cada linea
    lineaa.set_ydata([ya[i], 0])
    lineaa.set_xdata([xa[i], xa[i]])
    lineab.set_ydata([0, fx(xb[i])])
    lineab.set_xdata([xb[i], xb[i]])
    # Aproximacion con tangente
    b0 = ya[i] - dfi[i]*xa[i]
    tangentei = dfi[i]*xi+b0
    lineatanx.set_ydata(tangentei)
    
    return (puntoa, puntob, lineaa, lineab,lineatanx,)

# Limpia trama anterior
def limpiatrama():
    puntoa.set_ydata(np.ma.array(xa, mask=True))
    puntob.set_ydata(np.ma.array(xb, mask=True))
    lineaa.set_ydata(np.ma.array([0,0], mask=True))
    lineab.set_ydata(np.ma.array([0,0], mask=True))
    lineatanx.set_ydata(np.ma.array(xi, mask=True))
    return (puntoa, puntob, lineaa, lineab,lineatanx,)

# contador de tramas
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(fig_ani,unatrama,
                              i ,
                              fargs=(xa, ya,
                                     xb, dfi),
                              init_func=limpiatrama,
                              interval=retardo,
                              blit=True)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_animado.gif', writer='imagemagick')
#ani.save(narchivo+'.mp4')
plt.show()

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]

Método del Punto Fijo con gráfico animado en Python

Instrucciones en Python

# Algoritmo de punto fijo, Tabla
# Los valores de [a,b] son seleccionados
# desde la gráfica de la función
# error = tolera

import numpy as np

def puntofijo_tabla(gx,a,tolera, iteramax=20,
                    vertabla=True, precision=6):
    '''g(x) se obtiene al despejar una x de f(x)
    máximo de iteraciones predeterminado: iteramax
    si no converge hasta iteramax iteraciones
    la respuesta es NaN (Not a Number)
    '''
    itera = 0
    b = gx(a)
    tramo = abs(b-a)
    tabla = [[a,b,tramo]]
    if vertabla==True:
        print('método del Punto Fijo')
        print('i', ['xi','gi','tramo'])
        np.set_printoptions(precision)
        print(itera,np.array([a,b,tramo]))
    while(tramo>=tolera and itera<=iteramax):
        a = b
        b = gx(a)
        tramo = abs(b-a)
        itera = itera + 1
        if vertabla==True:
            print(itera,np.array([a,b,tramo]))
        tabla.append([a,b,tramo])
    respuesta = b
    # Valida respuesta
    if itera>=iteramax:
        respuesta = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    tabla = np.array(tabla,dtype=float)
    return(respuesta,tabla)

# PROGRAMA ----------------------

# INGRESO
fx = lambda x: np.exp(-x) - x
gx = lambda x: np.exp(-x)

a = 0
b = 1
tolera = 0.001

# PROCEDIMIENTO
[raiz,tabla] = puntofijo_tabla(gx,a,tolera, vertabla=True)

# SALIDA
print('raiz en :', raiz)

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
gi = gx(xi)
yi = xi

plt.plot(xi,fi, label='f(x)',
         linestyle='dashed')
plt.plot(xi,gi, label='g(x)')
plt.plot(xi,yi, label='y=x')

plt.axvline(raiz, color='magenta',
            linestyle='dotted')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Punto Fijo')
plt.grid()
plt.legend()
#plt.show()

# GRAFICA CON ANIMACION ------------
#import matplotlib.pyplot as plt
import matplotlib.animation as animation

xc = tabla[:,0]
yc = tabla[:,1]

# Inicializa parametros de trama/foto
narchivo = 'PuntoFijo' # nombre archivo
retardo = 700 # milisegundos entre tramas
tramas = len(xc)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
dx = np.abs(b-a)
dy = np.abs(gx(b)-gx(a))
graf_ani.set_xlim([a-0.05*dx,b+0.05*dx])
graf_ani.set_ylim([np.min(fi)-0.05*dy,np.max(fi)+0.05*dy])

# Lineas y puntos base
puntoa,  = graf_ani.plot(xc[0], yc[0], 'ro')
puntob,  = graf_ani.plot(xc[0], xc[0], 'go') # y=x
lineafx, = graf_ani.plot(xi,fi, color='blue',
                     linestyle='dashed', label='f(x)')
lineagx, = graf_ani.plot(xi,gi, color='orange', label='g(x)')
lineayx, = graf_ani.plot(xi,yi, color='green', label='y=x')
linearaiz = graf_ani.axvline(raiz, color='magenta',linestyle='dotted')

# Configura gráfica
linea0 = graf_ani.axhline(0, color='k')
graf_ani.set_title('Punto Fijo')
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Cada nueva trama
def unatrama(i,xc,yc):
    # actualiza cada punto
    puntoa.set_xdata(xc[i])
    puntoa.set_ydata(yc[i])
    puntob.set_xdata(xc[i]) # y=x
    puntob.set_ydata(xc[i])
    
    # actualiza cada flecha
    dx = xc[i+1]-xc[i]
    dy = yc[i]-xc[i]
    flecha01 = graf_ani.arrow(xc[i],xc[i], 0,dy,
              length_includes_head = True,
              head_width = 0.05*abs(dy),
              head_length = 0.1*abs(dy))
    flecha02 = graf_ani.arrow(xc[i],yc[i], dx,0,
              length_includes_head = True,
              head_width = 0.05*abs(dx),
              head_length = 0.1*abs(dx))
    return (puntoa, puntob, flecha01, flecha02)

# Limpia trama anterior
def limpiatrama():
    puntoa.set_ydata(np.ma.array(xc[0], mask=True))
    puntob.set_ydata(np.ma.array(xc[0], mask=True))
    return (puntoa, puntob)

# contador de tramas
i = np.arange(0, tramas-1,1)
ani = animation.FuncAnimation(fig_ani,unatrama,
                              i ,
                              fargs=(xc, yc),
                              init_func=limpiatrama,
                              interval=retardo,
                              blit=True)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_animado.gif', writer='imagemagick')
#ani.save(narchivo+'.mp4')
plt.show()

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]

Método de la Secante con gráfico animado en Python

Instrucciones en Python

# Método de la secante
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)
import numpy as np

def secante_raiz_tabla(fx,a,b,tolera, iteramax=20,
                 vertabla=True, precision=6):
    '''fx en forma numérica lambda
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    '''
    xi_1 = a
    xi = b
    itera = 0
    tramo = np.abs(xi-xi_1)
    tabla = []
    if vertabla==True:
        print('método de la Secante')
        print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo')
        np.set_printoptions(precision)
    while not(tramo<tolera or itera>iteramax):
        fi_1 = fx(xi_1)
        fi = fx(xi)
        xi1 = xi-fi*(xi_1 - xi)/(fi_1-fi)
        tramo = np.abs(xi1-xi)
        if vertabla==True:
            print(itera,np.array([xi_1,xi,xi1,fi_1,fi]),tramo)
        tabla.append([xi_1,xi,xi1,fi_1,fi])
        xi_1 = xi
        xi = xi1
        itera = itera + 1
    if itera>=iteramax:
        xi = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    respuesta = xi
    tabla = np.array(tabla,dtype=float)
    return(respuesta,tabla)

# PROGRAMA ----------------------

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10

a = 1
b = 4
c = (a+b)/2
tolera = 0.001
tramos = 100

# PROCEDIMIENTO
[raiz,tabla] = secante_raiz_tabla(fx,c,b,tolera,
                                  vertabla=True)
# SALIDA
print('raiz en :', raiz)

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
xc = tabla[:,2]
yc = fx(xc)

plt.plot(xi,fi, label='f(x)')
plt.plot([a,b],[fx(a),fx(b)],'o',
         color='red',label='[x0,f(x0)]')
plt.scatter(xc,yc,color='orange', label='[c,f(c)]')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
#plt.show()


# GRÁFICO CON ANIMACION ######
import matplotlib.animation as animation

xa = tabla[:,0]
ya = tabla[:,3]
xb = tabla[:,1]
yb = tabla[:,4]
xc = tabla[:,2]

# Inicializa parametros de trama/foto
narchivo = 'SecanteMetodo' # nombre archivo
retardo = 700 # milisegundos entre tramas
tramas = len(xa)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
graf_ani.set_xlim([a,b])
graf_ani.set_ylim([np.min(fi),np.max(fi)])

# Lineas y puntos base
lineafx, = graf_ani.plot(xi,fi,label ='f(x)')

puntoa, = graf_ani.plot(xa[0], ya[0],'o',
                        color='red', label='x[i-1]')
puntob, = graf_ani.plot(xb[0], yb[0],'o',
                        color='green', label='x[i]')
puntoc, = graf_ani.plot(xc[0], yc[0],'o',
                        color='orange', label='x[i+1]')

lineatan1, = graf_ani.plot([xa[0],xb[0]],
                           [ya[0],yb[0]],
                           color='orange',label='secante ac')
lineatan2, = graf_ani.plot([xc[0],xb[0]],
                           [0,yb[0]],
                           color='orange',label='secante cb')
linea_a, = graf_ani.plot([xa[0],xa[0]],
                         [ya[0],0], color='magenta',
                         linestyle='dashed')
linea_b, = graf_ani.plot([xb[0],xb[0]],
                         [0,yb[0]], color='magenta',
                         linestyle='dashed')
# Configura gráfica
linea0 = graf_ani.axhline(0, color='k')
graf_ani.set_title('Método de la Secante')
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Cada nueva trama
def unatrama(i,xa,ya,xb,yb,xc):
    # actualiza cada punto
    puntoa.set_xdata(xa[i]) 
    puntoa.set_ydata(ya[i])
    puntob.set_xdata(xb[i])
    puntob.set_ydata(yb[i])
    puntoc.set_xdata(xc[i])
    puntoc.set_ydata(0)
    # actualiza cada linea
    linea_a.set_ydata([ya[i], 0])
    linea_a.set_xdata([xa[i], xa[i]])
    linea_b.set_ydata([0, yb[i]])
    linea_b.set_xdata([xb[i], xb[i]])
    lineatan1.set_ydata([ya[i], 0])
    lineatan1.set_xdata([xa[i], xc[i]])
    lineatan2.set_ydata([0, yb[i]])
    lineatan2.set_xdata([xc[i], xb[i]])

    return (puntoa, puntob, puntoc,
            linea_a, linea_b,
            lineatan1, lineatan2,)

# Limpia trama anterior
def limpiatrama():
    puntoa.set_ydata(np.ma.array(xa, mask=True))
    puntob.set_ydata(np.ma.array(xb, mask=True))
    puntoc.set_ydata(np.ma.array(xc, mask=True))
    linea_a.set_ydata(np.ma.array([0,0], mask=True))
    linea_b.set_ydata(np.ma.array([0,0], mask=True))
    lineatan1.set_ydata(np.ma.array([0,0], mask=True))
    lineatan2.set_ydata(np.ma.array([0,0], mask=True))
    return (puntoa, puntob, puntoc,
            linea_a, linea_b,
            lineatan1, lineatan2,)

# contador de tramas
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(fig_ani,unatrama,
                              i ,
                              fargs=(xa, ya,
                                     xb, yb,
                                     xc),
                              init_func=limpiatrama,
                              interval=retardo,
                              blit=True)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_animado.gif', writer='imagemagick')
#ani.save(narchivo+'.mp4')
plt.show()

GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]

2017-09-022024-09-28

2.6 Sistemas de Ecuaciones no lineales – Newton-Raphson

Referencia: Chapra 6.5 p162, Chapra Ejercicio 6.11 p166

Con el método de Newton-Raphson para múltiples ecuaciones, determine las raíces para:

x^2+xy =10

y + 3xy^2 = 57

Observe que un par correcto de raíces es x=2 y y=3.
Use como valores iniciales x=1.5, y=3.5

Planteamiento

Las ecuaciones se expresan de la forma f(x,y) = 0

x^2+xy -10 = 0

y + 3xy^2 -57 = 0

Se puede usar extensiones de los métodos abiertos para resolver ecuaciones simples, por ejemplo Newton-Raphson.

u_{i+1} = u_i + (x_{i+1}-x_i)\frac{\partial u_i}{\partial x} + (y_{i+1}-y_i) \frac{\partial u_i}{\partial y}

v_{i+1} = v_i + (x_{i+1}-x_i)\frac{\partial v_i}{\partial x} + (y_{i+1}-y_i) \frac{\partial v_i}{\partial y}

ecuaciones que se pueden reordenar y encontrar la solución a partir de la matriz Jacobiano.

Instrucciones en Python

Usando un algoritmo para resolver el Jacobiano y estimar los puntos luego de cada iteración se obtienen:

iteración:  1
Jacobiano con puntos iniciales: 
[ 6.5   1.5 ]
[           ]
[36.75  32.5]
determinante:  156.12499999999994
puntos xi,yi: 2.03602882305845 2.84387510008006
error: 0.656124899919936
iteración:  2
Jacobiano con puntos iniciales: 
[6.91593274619696  2.03602882305845]
[                                  ]
[24.2628767545662  35.7412700376474]
determinante:  197.78430344142245
puntos xi,yi: 1.99870060905582 3.00228856292451
error: 0.158413462844444
iteración:  3
Jacobiano con puntos iniciales: 
[6.99968978103616  1.99870060905582]
[                                  ]
[27.0412098452019  37.0040558756713]
determinante:  204.96962918261596
puntos xi,yi: 1.99999998387626 2.99999941338891
error: 0.00228914953559523
iteración:  4
Jacobiano con puntos iniciales: 
[6.99999938114143  1.99999998387626]
[                                  ]
[26.9999894410015  36.9999926704397]
determinante:  204.9999473486533
puntos xi,yi: 1.99999999999998 3.00000000000008
error: 5.86611161867978e-7
Resultado: 
1.99999999999998 3.00000000000008

Algoritmo presentado para dos ecuaciones y dos incógnitas, en la unidad 3 se puede ampliar la propuesta. Revisar el método de Gauss-Seidel y Jacobi.

# Ejercicio Chapra Ej:6.11
# Sistemas de ecuaciones no lineales
# con método de Newton Raphson para xy

import numpy as np
import sympy as sym

def matrizJacobiano(variables, funciones):
    n = len(funciones)
    m = len(variables)
    # matriz Jacobiano inicia con ceros
    Jcb = sym.zeros(n,m)
    for i in range(0,n,1):
        unafi = sym.sympify(funciones[i])
        for j in range(0,m,1):
            unavariable = variables[j]
            Jcb[i,j] = sym.diff(unafi, unavariable)
    return Jcb

# PROGRAMA ----------
# INGRESO
x = sym.Symbol('x')
y = sym.Symbol('y')

f1 = x**2 + x*y - 10
f2 = y + 3*x*(y**2)-57

x0 = 1.5
y0 = 3.5

tolera = 0.0001

# PROCEDIMIENTO
funciones = [f1,f2]
variables = [x,y]
n = len(funciones)
m = len(variables)

Jxy = matrizJacobiano(variables, funciones)

# valores iniciales
xi = x0
yi = y0

# tramo inicial, mayor que tolerancia
itera = 0
tramo = tolera*2

while (tramo>tolera):
    J = Jxy.subs([(x,xi),(y,yi)])

    # determinante de J
    Jn = np.array(J,dtype=float)
    determinante =  np.linalg.det(Jn)

    # iteraciones
    f1i = f1.subs([(x,xi),(y,yi)])
    f2i = f2.subs([(x,xi),(y,yi)])

    numerador1 = f1i*Jn[n-1,m-1]-f2i*Jn[0,m-1]
    xi1 = xi - numerador1/determinante
    numerador2 = f2i*Jn[0,0]-f1i*Jn[n-1,0]
    yi1 = yi -numerador2/determinante
    
    tramo = np.max(np.abs([xi1-xi,yi1-yi]))
    xi = xi1
    yi = yi1

    itera = itera +1
    print('iteración: ',itera)
    print('Jacobiano con puntos iniciales: ')
    sym.pprint(J)
    print('determinante: ', determinante)
    print('puntos xi,yi:',xi,yi)
    print('error:',tramo)
    
# SALIDA
print('Resultado: ')
print(xi,yi)

2017-09-022024-09-30

2.5.1 Método de la Secante – Ejemplo con Python

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

1. Ejercicio

Referencia: Burden 2.1 ejemplo 1 p38

La ecuación mostrada tiene una raíz en el intervalo [1,2], ya que f(1) = -5 y f(2) = 14
Muestre los resultados parciales del algoritmo de la secante con una tolerancia de 0.0001

f(x) = x^3 + 4x^2 -10 =0

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]
..

2. Desarrollo Analítico

siendo:

f(x) = x^3 + 4x^2 -10 =0

x_{i+1}= x_i - f(x_i)\frac{(x_{i-1} - x_i)}{f(x_{i-1}) - f(x_i)}

Se probará con valores iniciales que tienen el mismo signo f(x[i-1]), f(x[i]), que no se considera en el método cerrado de la posición falsa

itera = 0

X_-1 = a =2.5, X₀ =b=4, tolera = 0.001

f(2.5) = (2.5)^3 + 4(2.5)^2 -10 = 30.625

f(4) = (4)^3 + 4(4)^2 -10 =118

x_{1}= 4 - 118\frac{(2.5 - 4)}{(30.625 - 118)} = 1.9742

errado = |1.9742 - 4| = 2.02575

itera = 1

X₀ = 4, X₁ = 1.9742

f(4) =118

f(1.9742) = ( 1.9742)^3 + 4( 1.9742)^2 -10 =13.2855

x_{2}= 1.9742 - (13.2855)\frac{(4 - 1.9742)}{(118 -13.2855)} =1.7172

errado = |1.7172 - 1.9742| = 0.2570

itera = 2

X₁ =1.9742, X₂ =1.7172

f(1.9742) = 13.2855

f(1.7172) = (1.7172)^3 + 4(1.7172)^2 -10 =6.8594

x_{3}= 1.7172 - (6.8594)\frac{(1.9742 - 1.7172)}{(6.8594 -13.2855)} = 1.4428

errado = | 1.4428- 1.7172| =0.2743

desarrollando una tabla con el algoritmo se tiene:

método de la Secante
i [ x[i-1], xi, x[i+1], f[i-1], fi ] tramo
0 [  2.5    4.       1.974249  30.625   118.      ] 2.0257510729613735
1 [  4.     1.974249 1.717233 118.       13.285584] 0.2570160557153698
2 [1.974249 1.717233 1.442883  13.285584  6.859484] 0.27434949602777015
3 [1.717233 1.442883 1.376796   6.859484  1.331607] 0.06608786561380797
4 [1.442883 1.376796 1.365656   1.331607  0.19207 ] 0.011139180030541596
5 [1.376796 1.365656 1.365232   0.19207   0.007041] 0.00042390961991034537
raiz en : 1.3652324200312267

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

3. Algoritmo en Python

El algoritmo básico a usar es:

# Método de secante
import numpy as np

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10
a = 1
b = 4
tolera = 0.001
iteramax = 20
precision = 5

c = (a+b)/2 # probar dos puntos en un mismo lado de f(x)
# PROCEDIMIENTO
xi_1 = c
xi = b
itera = 0
tramo = np.abs(xi-xi_1)
print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo')
np.set_printoptions(precision)
while not(tramo<tolera or itera>iteramax):
    fi_1 = fx(xi_1)
    fi = fx(xi)
    xi1 = xi-fi*(xi_1 - xi)/(fi_1-fi)
    tramo = np.abs(xi1-xi)
    print(itera,np.array([xi_1,xi, xi1, fi_1,fi]),tramo)
    xi_1 = xi
    xi = xi1
    itera = itera + 1

respuesta = xi

# SALIDA
print('raiz: ',respuesta)

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

4. Función en Python

Una función resumida, se recomienda realizar la validación de cambio de signo entre [a,b]

# Método de secante
import numpy as np

def secante_raiz(fx,a,b,tolera, iteramax=20,
                 vertabla=True, precision=6):
    '''fx en forma numérica lambda
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    '''
    xi_1 = a
    xi = b
    itera = 0
    tramo = np.abs(xi-xi_1)
    if vertabla==True:
        print('método de la Secante')
        print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo')
        np.set_printoptions(precision)
    while not(tramo<tolera or itera>iteramax):
        fi_1 = fx(xi_1)
        fi = fx(xi)
        xi1 = xi-fi*(xi_1 - xi)/(fi_1-fi)
        tramo = np.abs(xi1-xi)
        if vertabla==True:
            print(itera,np.array([xi_1,xi,xi1,fi_1,fi]),tramo)
        xi_1 = xi
        xi = xi1
        itera = itera + 1
    if itera>=iteramax:
        xi = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    respuesta = xi
    
    return(respuesta)

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10
a = 1
b = 4
tolera = 0.001
c = (a+b)/2 # probar dos puntos en un mismo lado de f(x)

# PROCEDIMIENTO
respuesta = secante_raiz(fx,c,b,tolera,
                         vertabla=True,precision = 5)
# SALIDA
print('raíz en: ', respuesta)

Scipy.optimize.newton – Secante

El método de la secante se encuentra implementado en Scipy en la forma de algoritmo de newton, que al no proporcionar la función para la derivada de f(x), usa el método de la secante:

>>> import scipy.optimize as opt
>>> opt.newton(fx,xa, tol=tolera)
1.3652320383201266

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2017-09-022024-10-08

2.5 Método de la Secante – Concepto

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

Método de la Secante

Referencia: Chapra 6.3 p154, Burden 2.3 p54,

El método de la secante busca evitar un posible inconveniente en el desarrollo el algoritmo para método de Newton-Raphson que es el implementar la evaluación de la expresión y valor de la primera derivada.

La derivada de la función f(x) también se puede aproximar mediante una diferencia finita dividida hacia atrás:

f'(x_i) = \frac{f(x_{i-1})-f(x_i)}{x_{i-1}-x_i}

la que se sustituye en la ecuación del método de Newton-Raphson para obtener:

x_{i+1}= x_i - f(x_i)\frac{(x_{i-1} - x_i)}{f(x_{i-1}) - f(x_i)}

Los métodos de la secante y de la falsa posición tienen ecuaciones idénticas, usan dos valores iniciales x[i-1] , x[i], para proyectar el nuevo valor de x[i+1].

Sin embargo, existe una diferencia importante entre ambos métodos en la forma en que uno de los valores iniciales se reemplaza por la nueva aproximación.

En el método de la falsa posición, la última aproximación de la raíz reemplaza cualquiera de los valores iniciales que dé un valor de la función con el mismo signo. En consecuencia, las dos aproximaciones siempre encierran a la raíz, es un método cerrado y siempre converge.

En el método de la secante se reemplaza los valores en secuencia estricta: con el nuevo valor x[i+1] se reemplaza a xi y xi reemplaza a x[i – 1]. Por lo que, algunas veces los dos valores están en el mismo lado de la raíz y en ciertos casos esto puede llevar a divergencias.

Observación: ¿Cuál es la diferencia con el método de Newton-Raphson?

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2017-09-022024-10-04

2.4.1 Método del Punto fijo – Ejemplo con Python

[ Punto fijo ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

1. Ejercicio

Referencia: Burden 2.2 p41, Chapra 6.1 p143, Rodríguez 3.2 p44

Encontrar la solución a la ecuación, usando el método del punto fijo, considerando tolerancia de 0.001

f(x): e^{-x} - x = 0

[ Punto fijo ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2. Desarrollo Analítico

Al igual que los métodos anteriores, es conveniente determinar el intervalo [a,b] donde es posible evaluar f(x). Se revisa si hay cambio de signo en el intervalo para buscar una raíz. Para el ejemplo, el rango de observación será [0,1], pues f(0)=1 es positivo y f(1)=-0.63 es negativo.

Para el punto fijo, se reordena la ecuación para para tener una ecuación con la variable independiente separada. Se obtiene por un lado la recta identidad y=x, por otro se tiene la función g(x).

f(x): e^{-x} - x = 0

x = e^{-x}

$g(x) = e^{-x}$

Se buscará la intersección entre las dos expresiones .

Se puede iniciar la búsqueda por uno de los extremos del rango [a,b].

iteración 1

– iniciando desde el extremo izquierdo x=a,

x_0 = 0

– se determina el valor de b = g(x) ,

x_1 = g(0) = e^{-0} = 1

– se determina la diferencia de la aproximación o error = |b-a|

tramo =|1-0|= 1

– se proyecta en la recta identidad, como el nuevo punto de evaluación
x=b.

– se repite el proceso para el nuevo valor de x, hasta que el error sea menor al tolerado. En caso que el proceso no converge, se utiliza un contador de iteraciones máximo, para evitar tener un lazo infinito.

iteración 2

x_1 = 1

x_2 = g(1) = e^{-1} = 0.3678

tramo =|0.3678 - 1|= 0.6322

iteración 3

x_2 = 0.3678

x_3 = e^{-0.3678} = 0.6922

tramo =|0.6922-0.3678|= 0.3244

La tabla resume los valores de las iteraciones

Método del punto fijo
iteración	x	xnuevo = g(x)	\|error\|
1	0	1.0	1
2	1.0	*0.3678*	0.6322
3	*0.3678*	0.6922	0.3244
4	0.6922	…
5

El proceso realizado en la tabla se muestra en la gráfica, para una función que converge.

[ Punto fijo ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

3. Algoritmo en Python

El algoritmo en Python del video se adjunta para seguimiento. Se requiere la función gx, el punto inicial y la tolerancia, la variable de número de iteraciones máxima, iteramax, permite controlar la convergencia de la función con el método.

El resultado del algoritmo se presenta como:

raíz en:  0.5669089119214953
errado :  0.0006477254067881466
itera  :  14

Instrucciones en Python

# Algoritmo de punto fijo
# [a,b] son seleccionados desde la gráfica
# error = tolera

import numpy as np

# INGRESO
fx = lambda x: np.exp(-x) - x
gx = lambda x: np.exp(-x)

a = 0
b = 1
tolera = 0.001
iteramax = 15

# PROCEDIMIENTO
i = 1 # iteración
b = gx(a)
tramo = abs(b-a)
while not(tramo<=tolera or i>iteramax):
    a = b
    b = gx(a)
    tramo = abs(b-a)
    i = i + 1
respuesta = b
# Valida convergencia
if (i>=iteramax):
    respuesta = np.nan

# SALIDA
print('raíz en: ', respuesta)
print('errado : ', tramo)
print('itera  : ', i)

Para obtener la gráfica básica se determinan los puntos para cada función fx y gx. Como los valore de a y b cambiaron durante el algoritmo, para la siguiente sección es necesario volver a escribirlos u obtener una copia de los valores en otra variable para reutilizarlos en ésta sección.

Se añaden las siguiente instrucciones al algoritmo anterior:

# GRAFICA
import matplotlib.pyplot as plt
# calcula los puntos para fx y gx
a = 0
b = 1
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
gi = gx(xi)
yi = xi

plt.plot(xi,fi, label='f(x)',
         linestyle='dashed')
plt.plot(xi,gi, label='g(x)')
plt.plot(xi,yi, label='y=x')

plt.axvline(respuesta, color='magenta',
            linestyle='dotted')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Punto Fijo')
plt.grid()
plt.legend()
plt.show()

[ Punto fijo ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

4. Función en Python

El resultado del algoritmo como una función y mostrando la tabla de resultados por iteraciones es:

método del Punto Fijo
i ['xi', 'gi', 'tramo']
0 [0. 1. 1.]
1 [1.       0.367879 0.632121]
2 [0.367879 0.692201 0.324321]
3 [0.692201 0.500474 0.191727]
4 [0.500474 0.606244 0.10577 ]
5 [0.606244 0.545396 0.060848]
6 [0.545396 0.579612 0.034217]
7 [0.579612 0.560115 0.019497]
8 [0.560115 0.571143 0.011028]
9 [0.571143 0.564879 0.006264]
10 [0.564879 0.568429 0.003549]
11 [0.568429 0.566415 0.002014]
12 [0.566415 0.567557 0.001142]
13 [0.567557 0.566909 0.000648]
raíz en:  0.5669089119214953

Instrucciones en Python

# Algoritmo de punto fijo
# [a,b] son seleccionados desde
# la gráfica de la función
# error = tolera

import numpy as np

def puntofijo(gx,a,tolera, iteramax=20,vertabla=True, precision=6):
    """
    g(x) se obtiene al despejar una x de f(x)
    máximo de iteraciones predeterminado: iteramax
    si no converge hasta iteramax iteraciones
    la respuesta es NaN (Not a Number)
    """
    itera = 0
    b = gx(a)
    tramo = abs(b-a)
    if vertabla==True:
        print('método del Punto Fijo')
        print('i', ['xi','gi','tramo'])
        np.set_printoptions(precision)
        print(itera,np.array([a,b,tramo]))
    while(tramo>=tolera and itera<=iteramax):
        a = b
        b = gx(a)
        tramo = abs(b-a)
        itera = itera + 1
        if vertabla==True:
            print(itera,np.array([a,b,tramo]))
    respuesta = b
    # Valida respuesta
    if itera>=iteramax:
        respuesta = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    return(respuesta)

# PROGRAMA ----------------------
# INGRESO
fx = lambda x: np.exp(-x) - x
gx = lambda x: np.exp(-x)

a = 0
b = 1
tolera = 0.001
iteramax = 15

# PROCEDIMIENTO
respuesta = puntofijo(gx,a,tolera,iteramax,vertabla=True)

# SALIDA
print('raíz en: ', respuesta)

De añadirse la parte gráfica, el bloque no requiere volver a escribir los valores de a y b, al ser usados como variable internas a la función y se mantienen en la parte principal del programa.

Scipy.optimize.fixed_point

El método del punto fijo se encuentra implementado en Scipy, que también puede ser usado de la forma:

>>> import scipy.optimize as opt
>>> opt.fixed_point(gx,a,xtol=0.001,maxiter=15)
array(0.5671432948307147)

el valor predeterminado de iteraciones si no se escribe es 500 y la tolerancia predeterminada es xtol=1e-08
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fixed_point.html

Tarea

Revisar lo que sucede cuando el valor inicial a esta a la derecha de la raíz.
Validar que la función converge, revisando que |g'(x)|<1, o que la función g(x) tenga pendiente menor a pendiente de la recta identidad.

[ Punto fijo ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2017-09-022024-11-04

2.4 Método del Punto fijo – Concepto

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

Método del Punto fijo

Referencia: Burden 2.2 p41, Chapra 6.1 p143, Rodríguez 3.2 p44

El método del punto fijo es un método abierto, también llamado de iteración de un punto o sustitución sucesiva, que reordena la ecuación

f(x)=0

de la forma en que x esté del lado izquierdo de la ecuación, para buscar la intersección entre la recta identidad y la curva g(x),

y = x

x=g(x)

Observe que la raíz de f(x) se encuentra en el mismo valor de x donde ocurre la intersección entre la recta identidad en color verde y la función g(x) en color naranja. Se usa la linea vertical en color morado en x=raíz como referencia de lo indicado.

El método consiste en establecer un punto inicia x₀ para la búsqueda, que se usa para calcular el valor g(x₀).

En la siguiente iteración el nuevo valor para x es g(x₀), que se refleja en la recta identidad y nuevamente se usa para calcular g(x).

El resultado iterativo se muestra en la figura animada, donde se observa que el resultado es convergente.

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

Ejemplo 1

f(x):e^{-x} - x = 0

se reordena para tener:

x = e^{-x}

g(x) = e^{-x}

Ejemplo 2

f(x): x^2 - 2x -3 = 0

se reordena para tener:

x = \frac {x^2 - 3}{2}

g(x) = \frac {x^2 - 3}{2}

Ejemplo 3

f(x): \sin (x) = 0

puede ser complicado despejar x, por lo que se simplifica el proceso sumando x en ambos lados.

x = \sin (x) + x

g(x) = \sin (x) + x

El método proporciona una fórmula para predecir un valor nuevo de x en función del valor anterior:

x_{i+1} = g(x_i)

con error aproximado calculado como:

\epsilon_a = \left| \frac{x_{i+1} - x_i}{x_{i+1}} \right| 100\%

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

Tarea

Plantee como usar los siguientes conceptos:

¿cuál sería el valor de tolerancia?
¿parámetros de inicio?
compare con con otro método conocido
Revisar el resultado cuando no se cumple que |g'(x)|<1

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2017-09-022024-09-29

2.3.1 Método de Newton-Raphson – Ejemplo con Python

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

1. Ejercicio

Referencia: Burden 2.1 ejemplo 1 p38

La ecuación mostrada tiene una raíz en [1,2], ya que f(1)=-5 y f(2)=14.
Muestre los resultados parciales del algoritmo de Newton-Raphson con una tolerancia de 0.0001

f(x) = x^3 + 4x^2 -10 =0

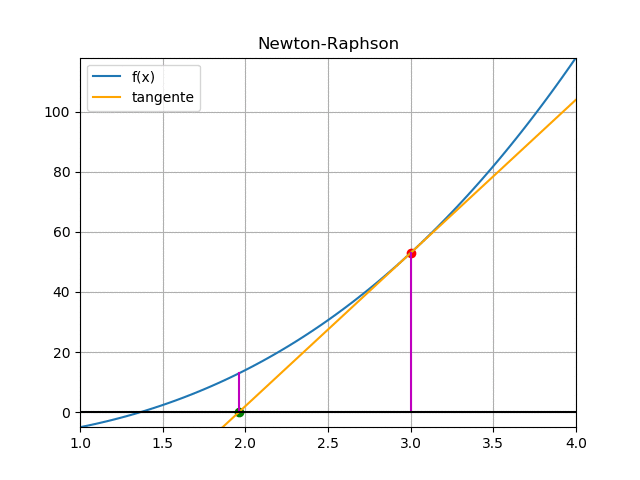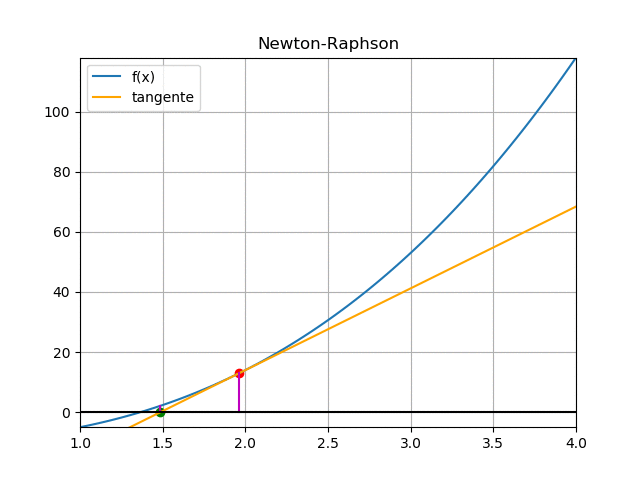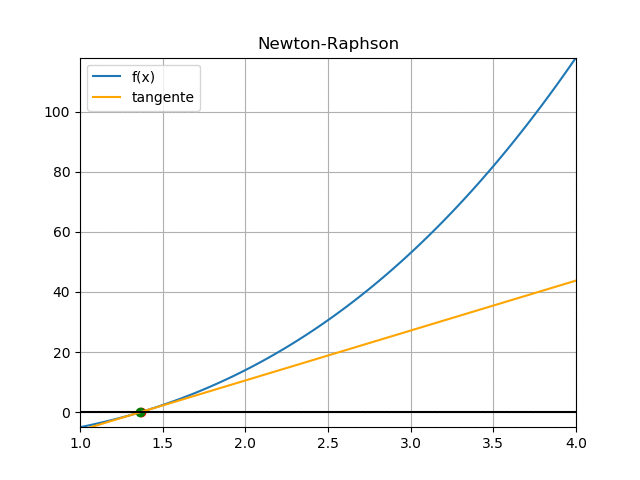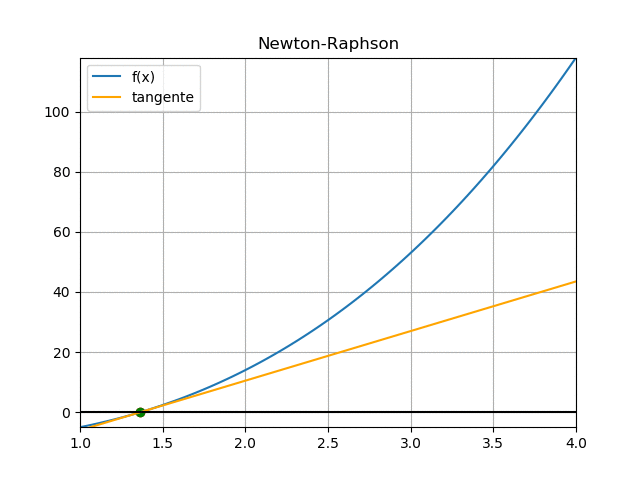
[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

2. Desarrollo Analítico

El método requiere obtener la derivada f'(x) de la ecuación para el factor del denominador.

f(x) = x^3 + 4x^2 -10

f'(x) = 3x^2 + 8x

x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}

Para el desarrollo se inicia la búsqueda desde un punto en el intervalo [1,2], por ejemplo el extremo derecho, x₁=2.

iteración 1

f(2) = (2)^3 + 4(2)^2 -10 = 14

f'(2) = 3(2)^2 + 8(2) = 28

x_{2} = 2 -\frac{14}{28} = 1.5

tramo = |2 -1.5| = 0.5

iteración 2

f(1.5) = (1.5)^3 + 4(1.5)^2 -10

= 2.375

f'(1.5) = 3(1.5)^2 + 8(1.5)

= 18.75

x_{3} = 1.5 -\frac{2.375}{18.75} = 1.3733

tramo = |1.5 -1.3733| = 0.1267

iteración 3

f(1.3733) = (1.3733)^3 + 4(1.3733)^2 -10

= 0.1337

f'(1.3733) = 3(1.3733)^2 + 8(1.3733)

= 16.6442

x_{4} = 1.3733 -\frac{0.1337}{16.6442}

=1.3652

tramo = |1.3733 -1.3652| = 0.0081

La tabla resume los valores de las iteraciones

Método de Newton-Raphson
iteración	x_i	x_nuevo	tramo
1	2	1.5	0.5
2	1.5	1.3733	0.1267
3	1.3733	1.3653	0.0081
4	…

Observe que el error representado por el tramo se va reduciendo entre cada iteración. Se debe repetir las iteraciones hasta que el error sea menor al valor tolerado.

Las demás iteraciones se dejan como tarea

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

3. Algoritmo con Python

El método de Newton-Raphson se implementa como algoritmo básico en Python

De la sección anterior, luego de realizar tres iteraciones para la tabla, notamos la necesidad de usar un algoritmo para que realice los cálculos repetitivos y muestre la tabla o directamente el resultado.

 ['xi', 'xnuevo', 'tramo']
[[2.0000 1.5000 5.0000e-01]
 [1.5000 1.3733 1.2667e-01]
 [1.3733 1.3653 8.0713e-03]
 [1.3653 1.3652 3.2001e-05]]
raiz en:  1.3652300139161466
con error de:  3.200095847999407e-05

Al algoritmo básico se les añade lo necesario para mostrar la tabla con los valores de las iteraciones.

# Método de Newton-Raphson
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)

import numpy as np

# INGRESO
fx  = lambda x: x**3 + 4*(x**2) - 10
dfx = lambda x: 3*(x**2) + 8*x

x0 = 2
tolera = 0.001

# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# SALIDA
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)

La gráfica presentada para revisar f(x) se realiza con las instrucciones:

# GRAFICA
import matplotlib.pyplot as plt
a = 1
b = 4
muestras = 21

xi = np.linspace(a,b,muestras)
fi = fx(xi)
plt.plot(xi,fi, label='f(x)')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

4. Función en Python

Se convierte el algoritmo a una función, con partes para ver la tabla, y se obtienen los siguientes resultados:

i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 2.  14.  28.   1.5  0.5]
1 [ 1.5     2.375  18.75    1.3733  0.1267]
2 [1.3733e+00 1.3435e-01 1.6645e+01 1.3653e+00 8.0713e-03]
3 [1.3653e+00 5.2846e-04 1.6514e+01 1.3652e+00 3.2001e-05]
raíz en:  1.3652300139161466

Instrucciones en Python

# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)

import numpy as np
import matplotlib.pyplot as plt

def newton_raphson(fx,dfx,xi, tolera, iteramax=100,
                   vertabla=False, precision=4):
    '''fx y dfx en forma numérica lambda
    xi es el punto inicial de búsqueda
    '''
    itera=0
    tramo = abs(2*tolera)
    if vertabla==True:
        print('método de Newton-Raphson')
        print('i', ['xi','fi','dfi', 'xnuevo', 'tramo'])
        np.set_printoptions(precision)
    while (tramo>=tolera):
        fi = fx(xi)
        dfi = dfx(xi)
        xnuevo = xi - fi/dfi
        tramo = abs(xnuevo-xi)
        if vertabla==True:
            print(itera,np.array([xi,fi,dfi,xnuevo,tramo]))
        xi = xnuevo
        itera = itera + 1

    if itera>=iteramax:
        xi = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')

    return(xi)

# INGRESO
fx  = lambda x: x**3 + 4*(x**2) - 10
dfx = lambda x: 3*(x**2) + 8*x

x0 = 2
tolera = 0.001

# PROCEDIMIENTO
respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True)
# SALIDA
print('raíz en: ', respuesta)

La gráfica se la puede añadir usando las instrucciones dadas en el algoritmo básico realizado al inicio par ala comprensión del método.

scipy.optimize.newton

El método de Newton-Raphson se encuentra implementado en Scipy, que también puede ser usado de la forma:

>>> import scipy.optimize as opt
>>> opt.newton(fx,x0, fprime=dfx, tol = tolera)
1.3652300139161466
>>>

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html

Tarea

Calcule la raíz de f(x) = e^-x – x, empleando como valor inicial x₀ = 0

convertir el algoritmo a una función
Revisar las modificaciones si se quiere usar la forma simbólica de la función.
incorpore la gráfica básica 2D de la función f(x)

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2017-09-022024-10-08

2.3 Método de Newton-Raphson – Concepto

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

Método de Newton-Raphson

Referencia: Burden 2.3 p49, Chapra 6.2 p148, Rodríguez 3.3 p52

Se deduce a partir de la interpretación gráfica o por medio del uso de la serie de Taylor.

De la gráfica, se usa el triángulo formado por la recta tangente que pasa por f(x_i), con pendiente f'(x_i) y el eje x.

f'(x_i) = \frac{f(x_i) - 0}{x_i - x_{i+1}}

El punto x_i+1 es la intersección de la recta tangente con el eje x, que es más cercano a la raíz de f(x), valor que es usado para la próxima iteración.

Reordenando la ecuación de determina la fórmula para el siguiente punto:

x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}

El error se determina como la diferencia entre los valores sucesivos encontrados |x_i+1 – x_i|

La gráfica animada muestra el proceso aplicado varias veces sobre f(x) para encontrar la raíz.

Tarea

Use la serie de Taylor hasta la primera derivada para encontrar el siguiente punto de aproximación x_i+1

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

2017-09-022024-09-29

2.2.1 Método de la Posición Falsa – Ejemplo con Python

[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

1. Ejercicio

Referencia: Burden 2.1 ejemplo 1 p38

La ecuación mostrada tiene una raíz en [1,2], ya que f(1)=-5 y f(2)=14. Muestre los resultados parciales del algoritmo de la posición falsa con una tolerancia de 0.0001

f(x) = x^3 + 4x^2 -10 =0

[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

2. Desarrollo Analítico

Semejante a los métodos anteriores, el método posición falsa, falsa posición, regla falsa o regula falsi, usa un intervalo [a,b] para buscar la raíz.

Se divide el intervalo en dos partes al calcular el punto c que divide al intervalo siguiendo la ecuación:

c = b - f(b) \frac{a-b}{f(a)-f(b)}

iteración 1

a = 1 , b = 2

f(1) = (1)^3 + 4(1)^2 -10 = -5

f(2) = (2)^3 + 4(2)^2 -10 = 14

c = 2 - 14 \frac{1-2}{-5-14} = 1.2631

f(1.2631) = (1.2631)^3 + 4(1.2631)^2 -10

= -1.6031

el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo

tramo = |c-a| = | 1.2631 - 1| = 0.2631

a = c = 1.2631

iteración 2

a = 1.2631 , b = 2

f(1.2631) = -1.6031

f(2) = 14

c = 2 - 14 \frac{1.2631-2}{-1.6031-14}

= 1.3388

f(1.3388) = (1.3388)^3 + 4(1.3388)^2 -10

= -0.4308

el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo

tramo = |c-a| = |1.3388 - 1.2631| = 0.0757

a = c = 1.3388

iteración 3

a = 1.3388 , b = 2

f(1.3388) = -0.4308

f(2) = 14

c = 2 - 14 \frac{1.3388-2}{-0.4308-14}

= 1.3585

f(1.3585) = (1.3585)^3 + 4(1.3585)^2 -10

= -0.1107

el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo

tramo = |c-a| = |1.3585 - 1.3388| = 0.0197

a = c = 1.3585

valores que se resumen en la tabla

Método de posición falsa
a	c	b	f(a)	f(c)	f(b)	tramo
1	1.2631	2	-5	-1.6031	14	0.2631
1.2631	1.3388	2	-1.6031	-0.4308	14	0.0757
1.3388	1.3585	2	-0.4308	-0.1107	14	0.0197
1.3585	…	2

se puede continuar con las iteraciones como tarea

[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

3. Algoritmo en Python

Algoritmo básico del video:

# Algoritmo Posicion Falsa para raices
# busca en intervalo [a,b]
import numpy as np

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10

a = 1
b = 2
tolera = 0.001

# PROCEDIMIENTO
tramo = abs(b-a)
while not(tramo<=tolera):
    fa = fx(a)
    fb = fx(b)
    c = b - fb*(a-b)/(fa-fb)
    fc = fx(c)
    cambia = np.sign(fa)*np.sign(fc)
    if (cambia > 0):
        tramo = abs(c-a)
        a = c
    else:
        tramo = abs(b-c)
        b = c
raiz = c

# SALIDA
print(raiz)

Algoritmo aumentado para mostrar la tabla de cálculos

# Algoritmo Posicion Falsa para raices
# busca en intervalo [a,b]
# tolera = error

import numpy as np

# INGRESO
fx = lambda x: x**3 + 4*(x**2) -10

a = 1
b = 2
tolera = 0.0001

# PROCEDIMIENTO
tabla = []
tramo = abs(b-a)
fa = fx(a)
fb = fx(b)
while not(tramo<=tolera):
    c = b - fb*(a-b)/(fa-fb)
    fc = fx(c)
    unafila = [a,c,b,fa,fc,fb,tramo]
    cambio = np.sign(fa)*np.sign(fc)
    if cambio>0:
        tramo = abs(c-a)
        a = c
        fa = fc
    else:
        tramo = abs(b-c)
        b = c
        fb = fc
    unafila[6]=tramo
    tabla.append(unafila)
tabla = np.array(tabla)
ntabla = len(tabla)

# SALIDA
np.set_printoptions(precision=6)
print('método de la Posición Falsa ')
print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
print('  ','tramo')
for i in range(0,ntabla,1):
    print(i, tabla[i,0:3],tabla[i,3:6])
    print('   ', tabla[i,6])

print('raiz:  ',c)

Observe el número de iteraciones realizadas, hasta presentar el valor de la raíz en 1.3652 con un error de 0.000079585 en la última fila de la tabla. Sin embargo, observe que la tabla solo muestra cálculos de filas completas, el último valor de c y error no se ingresó a la tabla, que se muestra como c y tramo, y es el más actualizado en los cálculos.

método de la Posición Falsa 
i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)']
   tramo
0 [1.       1.263158 2. ] [-5.       -1.602274 14. ]
   0.26315789473684204
1 [1.263158 1.338828 2. ] [-1.602274 -0.430365 14. ]
   0.0756699440909967
2 [1.338828 1.358546 2. ] [-0.430365 -0.110009 14. ]
   0.019718502996940224
3 [1.358546 1.363547 2. ] [-0.110009 -0.027762 14. ]
   0.005001098217311428
4 [1.363547 1.364807 2. ] [-2.776209e-02 -6.983415e-03  1.400000e+01]
   0.0012595917846898175
5 [1.364807 1.365124 2. ] [-6.983415e-03 -1.755209e-03  1.400000e+01]
   0.0003166860575976038
6 [1.365124 1.365203 2. ] [-1.755209e-03 -4.410630e-04  1.400000e+01]
    7.958577822231305e-05
raíz en:  1.3652033036626001

[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

4. Función en Python

# Algoritmo de falsa posicion para raices
# Los valores de [a,b] son seleccionados
# desde la gráfica de la función
# error = tolera

import numpy as np

def posicionfalsa(fx,a,b,tolera,iteramax = 20,
                        vertabla=False, precision=6):
    '''fx en forma numérica lambda
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    error = tolera
    '''
    fa = fx(a)
    fb = fx(b)
    tramo = np.abs(b-a)
    itera = 0
    cambia = np.sign(fa)*np.sign(fb)

    if cambia<0: # existe cambio de signo f(a) vs f(b)
        if vertabla==True:
            print('método de la Posición Falsa ')
            print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
            print('  ','tramo')
            np.set_printoptions(precision)

        while (tramo >= tolera and itera<=iteramax):
            c = b - fb*(a-b)/(fa-fb)
            fc = fx(c)
            cambia = np.sign(fa)*np.sign(fc)
            if vertabla==True:
                print(itera,np.array([a,c,b]),
                      np.array([fa,fc,fb]))
            if (cambia > 0):
                tramo = np.abs(c-a)
                a = c
                fa = fc
            else:
                tramo = np.abs(b-c)
                b = c
                fb = fc

            if vertabla==True:
                print('  ',tramo)
            itera = itera + 1
        respuesta = c
        # Valida respuesta
        if (itera>=iteramax):
            respuesta = np.nan
    else: 
        print(' No existe cambio de signo entre f(a) y f(b)')
        print(' f(a) =',fa,',  f(b) =',fb) 
        respuesta=np.nan

    return(respuesta)

# PROGRAMA ----------------------
# INGRESO
fx  = lambda x: x**3 + 4*x**2 - 10
a = 1
b = 2
tolera = 0.0001

# PROCEDIMIENTO
respuesta = posicionfalsa(fx,a,b,tolera,vertabla=True)
# SALIDA
print('raíz en: ', respuesta)

La gráfica se puede obtener añadiendo las siguientes instrucciones:

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21

xi = np.linspace(a,b,muestras)
fi = fx(xi)
plt.plot(xi,fi, label='f(x)')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()

[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]