2.5.1 Método de la Secante – Ejemplo con Python

Referencia: Burden ejemplo 1 p51

La ecuación mostrada tiene una raíz en el intervalo [1,2], ya que f(1) = -5 y f(2) = 14
Muestre los resultados parciales del algoritmo de la secante con una tolerancia de 0.0001

f(x) = x^3 + 4x^2 -10 =0

[xa ,	 xb , 	 xc , 	 tramo]
[ 1.5     1.504   1.3736  0.1264]
[ 1.3736  1.5     1.3658  0.0078]
[  1.3658e+00   1.3736e+00   1.3652e+00   5.2085e-04]
raiz en:  1.36523214292

El algoritmo a implementar es:

# Método de la secante
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)

import numpy as np

def secante_tabla(fx,xa,tolera):
    dx = 4*tolera
    xb = xa + dx
    tramo = dx
    tabla = []
    while (tramo>=tolera):
        fa = fx(xa)
        fb = fx(xb)
        xc = xa - fa*(xb-xa)/(fb-fa)
        tramo = abs(xc-xa)
        
        tabla.append([xa,xb,xc,tramo])
        xb = xa
        xa = xc

    tabla = np.array(tabla)
    return(tabla)

# PROGRAMA ---------------------
# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10

a  = 1
b  = 2
xa = 1.5
tolera = 0.001
tramos = 100

# PROCEDIMIENTO
tabla = secante_tabla(fx,xa,tolera)
n = len(tabla)
raiz = tabla[n-1,2]

# SALIDA
np.set_printoptions(precision=4)
print('[xa ,\t xb , \t xc , \t tramo]')
for i in range(0,n,1):
    print(tabla[i])
print('raiz en: ', raiz)

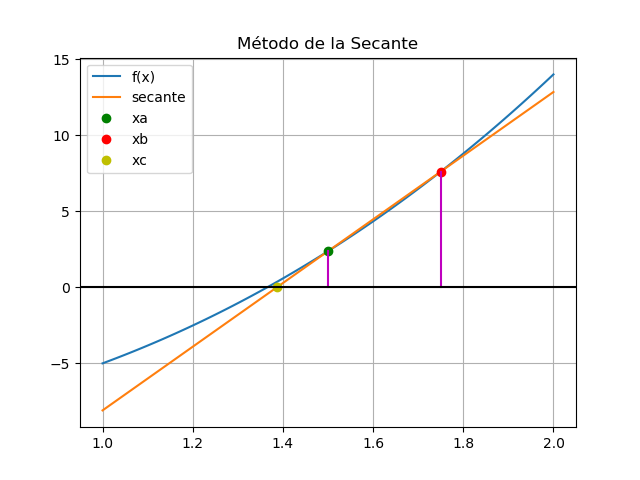
En el caso de añadir la gráfica para la primera iteración:

# GRAFICA
import matplotlib.pyplot as plt

# Calcula los puntos a graficar
xi = np.linspace(a,b,tramos+1)
fi = fx(xi)
dx = (b-xa)/2
pendiente = (fx(xa+dx)-fx(xa))/(xa+dx-xa)
b0 = fx(xa) - pendiente*xa
tangentei = pendiente*xi+b0

fxa = fx(xa)
xb = xa + dx
fxb = fx(xb)

plt.plot(xi,fi, label='f(x)')

plt.plot(xi,tangentei, label='secante')
plt.plot(xa,fx(xa),'go', label='xa')
plt.plot(xa+dx,fx(xa+dx),'ro', label='xb')
plt.plot((-b0/pendiente),0,'yo', label='xc')

plt.plot([xa,xa],[0,fxa],'m')
plt.plot([xb,xb],[0,fxb],'m')

plt.axhline(0, color='k')
plt.title('Método de la Secante')
plt.legend()
plt.grid()
plt.show()

---

Scipy.optimize.newton – Secante

El método de la secante se encuentra implementado en Scipy en la forma de algoritmo de newton, que al no proporcionar la función para la derivada de f(x), usa el método de la secante:

>>> import scipy.optimize as opt
>>> opt.newton(fx,xa, tol=tolera)
1.3652320383201266

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html

---

Tarea

convertir el algoritmo a una función de python con respuesta simple