raíces de ecuaciones – Página 5

2017-11-102023-02-04

1Eva_IT2010_T1_MN Demanda y producción sin,log

1ra Evaluación I Término 2010-2011. 6/Julio/2010. ICM02188 Métodos Numéricos

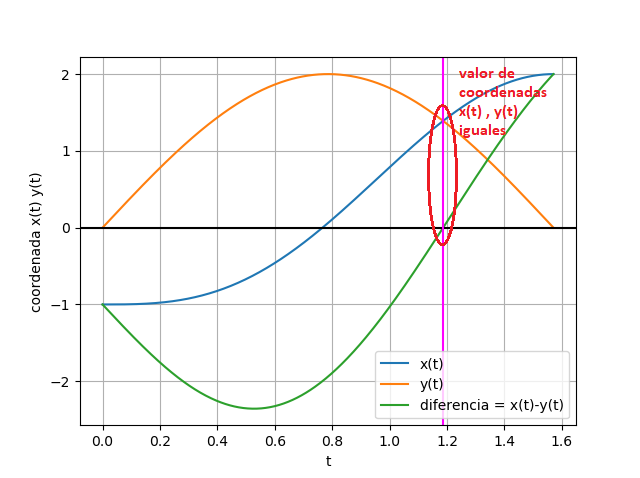
Tema 1. La demanda de un producto en el intervalo de tiempo [0,3] tiene forma sinusoidal.

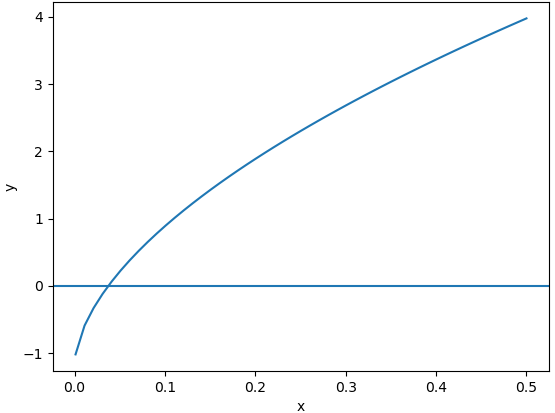
Al detectar la demanda, una empresa puede iniciar su producción a partir del instante 1, y la cantidad producida tiene forma logaritmica natural.

Se necesita encontrar el instante a partir del cual, la producción satisface a la demanda del producto.

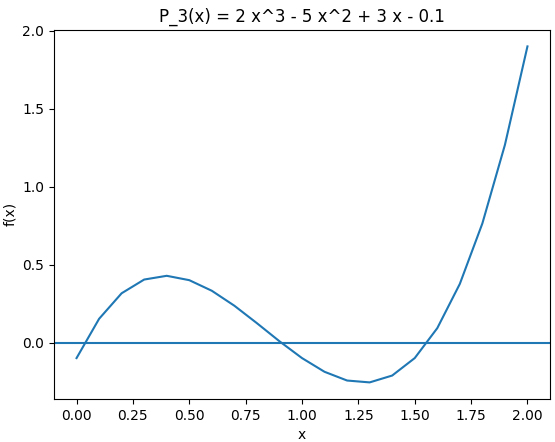
Use el método de la Bisección para localizar el intervalo de la respuesta y obtenga la respuesta con error menor a 0.01

2017-11-092023-02-04

1Eva_IIT2009_T1 Movimiento de partícula en plano

1ra Evaluación II Término 2009-2010. 1/Diciembre/2009. ICM00158

Tema 1. El movimiento de una partícula en el plano, se encuentra representado por las ecuaciones paramétricas:

x(t) = 3 \sin ^{3}(t)-1

y(t) = 4 \sin (t)\cos (t)

t \geq 0

Donde x, y son las coordenadas de la posición expresadas en cm y t se expresa en segundos.

a) Demuestre que existe un instante t ∈ [0, π/2] tal que sus coordenadas x e y coinciden.

b) Empleando el método de Newton, aproxime con una precisión de 10^-5 en qué instante de tiempo las dos coordenadas serán iguales en el intervalo dado en el literal a.

Referencias: Megaconstrucciones, El Tren InterUrbano | México – Toluca.

El Tunel debajo del agua entre Francia e Inglaterra

2017-11-092023-02-04

1Eva_IIT2009_T1_MN Precio de producto ln(x)

1ra Evaluación II Término 2009-2010. 1/Diciembre/2009. ICM02188 Métodos Numéricos

Tema 1. (30 puntos) Suponga que el precio de un producto f(x) depende de la cantidad disponible x, con la siguiente relación:

f(x) = 50 ln(x)

10 \leq x \leq 40

a) Determine la cantidad del producto para que el precio sea igual a 160.
Use el método de Newton con una precisión 10^-4,

b) Encuentre un intervalo [a, b] tal que para cualquier aproximación inicial que pertenezca a ese intervalo, el método de Newton converge en el literal anterior.

2017-11-092024-08-05

1Eva_IT2009_T1 Demanda de un producto alcanza la producción

1ra Evaluación I Término 2009-2010. 7/Julio/2009. ICM00158 y ICM02188 Métodos Numéricos

Tema 1. (30 puntos)
Se propone el siguiente modelo para describir la demanda de un producto, en donde t es tiempo en meses:

f(t) = 200 t e^{-0.75t}

a) Encuentre el primer valor de t para el cual la demanda alcanza el valor de 80 unidades.
Use el método de Newton para los cálculos.
Elija el valor inicial y muestre los valores intermedios.
Calcule la respuesta con cuatro decimales exactos.

b) Encuentre el valor de t para el cual la demanda alcanza el valor máximo.
Use el método de Newton para los cálculos .
Elija un valor inicial y muestre los valores intermedios.
Calcule la respuesta con cuatro decimales exactos.

2017-11-082024-09-27

1Eva_IIT2008_T1_MN Bacterias contaminantes

1ra Evaluación II Término 2008-2009. 9/Diciembre/2008. ICM02188 Métodos Numéricos

Tema 1. La concentración de bacterias contaminantes c en un lago decrece de acuerdo con la relación:

c= 70 e^{-1.5t} + 25 e^{-0.075t}

Se necesita determinar el tiempo para que la concentración de bacterias sea menor o igual a 9.

a) Encuentre un intervalo en el que exista una raíz de la ecuación

b) Elija un valor inicial del tiempo tal que el método de Newton-Raphson converja a la solución requerida.

c) Calcule la solución con el método de Newton-Raphson con una precisión de 0.001

Referencias: Contaminación del Agua – BrainPOP Español.

2017-11-082024-09-27

1Eva_IIT2008_T3 Bacterias contaminantes

1ra Evaluación II Término 2008-2009. 9/Diciembre/2008. ICM00158

Tema 3. La concentración de bacterias contaminantes c en un lago decrece de acuerdo con la relación:

c= 70 e^{-1.5t} + 25 e^{-0.075t}

Se necesita determinar el tiempo para que la concentración de bacterias se reduzca a 9 unidades o menos.

a) Determine un intervalo de existencia de la raíz de la ecuación. (Grafique)

b) Encuentre un valor de t tal que la convergencia del método de Newton-Raphson este garantizada.

c) Aproxime la raíz con el método de Newton-Raphson, indicando la cota del error.

Referencias: Contaminación del Agua – BrainPOP Español.

2017-11-082023-02-04

1Eva_IT2008_T1 Raíz de función(f)

1ra Evaluación I Término 2008-2009. 8/Julio/2008. ICM00158

Tema 1. Dada la fórmula:

\Big(\sqrt{f}\Big) ln \Bigg( R\frac{\sqrt{f}}{2.51} \Bigg) - 1.1513 = 0

Determinar el valor de f con un aproximación del orden de 10^-5 para R=5000

2017-11-072024-09-25

1Eva_IIIT2007_T3 Factorar polinomio

1ra Evaluación III Término 2007-2008. 3/Marzo/2008. ICM00158

Tema 3. Se requiere factorar el polinomio:

P_3(x) = 2x^3-5x^2 + 3x-0.1

P_3(x) = (x - r_1)(x - r_2)(x - r_3)

Utilizando el siguiente procedimiento:

a. Calcule r₁ resolviendo P₃(x) = 0 con Newton, ε = 0.0001

b. Obtenga el polinomio cociente Q₂(x), a partir de P₃(x) = (x – r₁)Q₂(x)

c. Calcule r₂ y r₃ de la ecuación Q₂(x) = 0

d. Escriba los otros factores de Q₂(x) = (x – r₂)(x – r₃)

Observe la gráfica del problema para la solución

2017-11-072024-09-16

1Eva_IIT2007_T1 Distribución Binomial acumulada

1ra Evaluación II Término 2007-2008. 4/Diciembre/2007. ICM00158

Tema 1. Un modelo de uso frecuente en teoría de probabilidad es la distribución binomial acumulada, cuya fórmula es:

F = \sum_{t=0}^{k} \binom{n}{t} p^t (1-p)^{n-t}

Con la fórmula de Newton-Raphson, calcule con cuatro decimales exactos el valor de p tal que F=0.4, dado que n=5 y k=1

Nota: El valor de p debe ser un número real entre 0 y 1

a. Plantear el ejercicio para encontrar h para un t dado, muestre el intervalo de búsqueda y una gráfica.

b. Desarrolle usando el método de Newton-Raphson para tres iteraciones y tolerancia milimétrica.

c. Verifique el orden de convergencia y observe sus resultados usando el algoritmo.

Rúbrica: Planteamiento (5 puntos), iteraciones y error (15 puntos), análisis de la convergencia (5 puntos). observación de resultados, algoritmo y gráficas adjuntos (5 puntos).