Edison Del Rosario – Fundamentos de Programación

El ejercicio se presenta desde la perspectiva que un sólido que se genera al rotar un área que se encuentra entre f(x) y el eje x.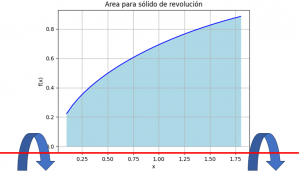

f(x) = \sqrt{\sin (x/2)}

El volumen del sólido de revolución se puede encontrar usando el integral

V = \int_{a}^{b} \pi (f(x))^2 dx

La gráfica del volumen de rotación se representa como: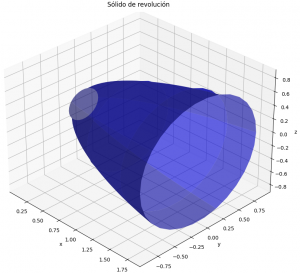

que se desarrolla usando la librería mpl_toolkits.mplot3d.axes3d

Se usa una figura(ventana) con una gráfica para 2D y otra figura para 3D

Instrucciones en Python

# 2Eva_2023PAOII_T1 Volumen por solido de revolución
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

# INGRESO
f = lambda x: np.sqrt(np.sin(x/2))

# eje x
xa = 0.1
xb = 1.8
xmuestras = 31
# angulo w de rotación
w_a = 0
w_b = 2*np.pi
w_muestras = 31

# PROCEDIMIENTO
# muestras en x
xi = np.linspace(xa, xb, xmuestras)

# grafica 2D para el area de corte en eje y,x
fi = f(xi)
f0 = np.zeros(xmuestras,dtype=float)

# grafica 3D muestras en x y angulo w
wi = np.linspace(w_a, w_b, w_muestras)
X, W = np.meshgrid(xi, wi)
# proyeccion en cada eje 
Yf = f(xi)*np.cos(W)
Zf = f(xi)*np.sin(W)

# SALIDA
# grafica 2D
figura2D = plt.figure()
grafica2D = figura2D.add_subplot(111)
grafica2D.plot(xi,fi,color='blue',label='f(x)')
grafica2D.fill_between(xi,fi,f0,color='lightblue')
grafica2D.grid()
grafica2D.set_title('Area para sólido de revolución')
grafica2D.set_xlabel('x')
grafica2D.set_ylabel('f(x)')

# grafica 3D
figura3D = plt.figure()
grafica = figura.add_subplot(111, projection='3d')

grafica.plot_surface(X, Yf, Zf,
                     color='blue', label='f(x)',
                     alpha=0.6, rstride=6, cstride=12)

grafica.set_title('Sólido de revolución')
grafica.set_xlabel('x')
grafica.set_ylabel('y')
grafica.set_zlabel('z')
# grafica.legend()
eleva = 30
rota = -45
deltaw = 5
grafica.view_init(eleva, rota)

# rotacion de ejes
for angulo in range(rota, 360+rota, deltaw ):
    grafica.view_init(eleva, angulo)
    plt.draw()
    plt.pause(.001)
plt.show()