U3videos1 Estructuras de Control en programación, Condicionales ‘If’ y Lazos/Bucles ‘While’
3Eva_IT2019_T3 Prueba de escritorio – cadenas, listas, segmentar, separar
3ra Evaluación I Término 2019-2020, Septiembre 13, 2019
Tema 3. (10 puntos) ¿Qué muestra el siguiente código? Justifique su respuesta
A = 'Num empresas,17,0|9|1,10|19|2,20|29|3' campos = A.split( ',') valores = [] for rango in campos[2:]: valores.append(int(rango.split('|')[0])) print(valores)
Asuma que este tema NO tiene errores de compilación. Si usted cree que hay algún error de compilación, consúltelo inmediatamente con su profesor.
s3Eva_IT2019_T3 Prueba de escritorio – cadenas, listas, segmentar, separar
3Eva_IT2019_T2 Juego del ahorcado
3ra Evaluación I Término 2019-2020, Septiembre 13, 2019
Tema 2. (30 puntos) 
Escriba un programa de Python que implemente un juego de adivinanzas de palabras.
Considere que para su programa ya están definidas las siguientes variables y función:
1. Una lista C de las categorías para el juego.
C = ['Transportes', 'Alimentos', 'Deportes', ...],
2. La función perteneceCategoria(palabra, categoria) que retorna True si palabra pertenece a la categoria, False en caso contrario.
3. El diccionario puntajes con el siguiente formato:
puntajes = {'Transportes':{'a':10, 't':4, 'f':5, ...},
'Deportes': {'a':3, 'z':5, 't':10, ...},
... }
Para la implementación del juego considere las siguientes reglas:
r1. El jugador tiene cinco turnos para jugar
Para cada turno:
r2. El programa selecciona aleatoriamente una categoría de la lista C
r3. El programa le pide al jugador que ingrese una palabra para la categoría seleccionada en el paso r2
r4. Si la palabra pertenece a la categoría dada y no ha sido ingresada en un turno anterior, calcule los puntos totales para la palabra.
El puntaje de la palabra es la suma de los puntajes de cada una de sus letras, de acuerdo al diccionario puntajes.
Una letra tendrá puntajes distintos dependiendo de la categoría del paso r2.
Si la palabra no cumple con las condiciones, el jugador no obtiene puntos en ese turno
r5. En cada turno, muestre el puntaje obtenido para la palabra ingresada y el puntaje acumulado
Al final de los cinco turnos:
r6. El jugador habrá ganado si completa un mínimo de 500 puntos, muestre el mensaje correspondiente “Ganó” o “Perdió”.
3Eva_IT2019_T1 Producción en hacienda
3ra Evaluación I Término 2019-2020, Septiembre 13, 2019
Tema 1. (60 puntos)
Asuma que tiene un archivo con la información de los productos agrícolas cosechados por una hacienda durante todos los días del año 2018.
La información se encuentra en el siguiente formato:
codigo1,codigo2,codigo3,...,codigoN codigo_producto,fecha(dd-MMM-aaaa),cantidad_cosechada
Ejemplo:
100034,100312,100021,...,201245,432198 codigo_producto,fecha(dd-MMM-aaaa),cantidad_cosechada 100034,02-ENE-2018,5 100021,02-ENE-2018,15 100021,07-ENE-2018,11 432198,20-ENE-2018,12 ...
Nota: La primera línea del archivo contiene los códigos de todos los productos agrícolas presentes en el resto del archivo, mientras que la segunda línea es la cabecera del archivo.
Implemente las siguientes funciones:
1.1. crearMatriz(nomArchivo) que recibe el nombre del archivo con la información de las cosechas de un año; y devuelve un vector con todos los códigos de productos y una matriz con los totales (valores enteros) de cosechas para cada producto (filas) durante cada mes del año (columnas). Ejemplo:
[ENE,FEB,MAR,ABR,MAY,JUN, JUL,AGO,SEP,OCT,NOV,DIC] |
|
Cod =[ |
M=[ |
1.2. mesMasRentable(M) que recibe la matriz de cosechas M . Esta función retorna el nombre del mes en que más se cosechó y el total de cosecha de ese mes.
1.3. altoBajos(M, k) que recibe la matriz de cosechas M y un entero k. La función retorna el nombre de todos los meses que tienen una cosecha total con al menos k unidades por debajo de la cosecha del mejor mes del año.
1.4. mejorTrimestre(M, Cod, codigo) que recibe la matriz de cosechas M, el vector de códigos Cod y el codigo de un producto. La función debe retornar el nombre del trimestre («T1», «T2», «T3» o «T4») en el que más se cosechó el producto con codigo .
1.5. mejoresNProductos(M, Cod, n) que recibe la matriz de cosechas M, el vector de códigos Cod y un número entero n . La función debe retornar los códigos de los n productos más cosechados durante el año.
1.6. promedioProductos(M, Cod, codigos) que recibe la matriz de cosechas M, el vector de códigos Cod y una lista con códigos de productos. La función retorna el promedio de los totales de cosecha entre los códigos dados en la lista.
7. porCategoria(M, Cod, categorias) que recibe la matriz de cosechas M , el vector de códigos Cod y un diccionario categorias con el siguiente formato:
categorias = {'legumbres':[100034,201245,...],
'verduras': [100021,200013,...],
... }
La función deberá escribir un archivo por cada categoría con el siguiente formato: Archivo_legumbres.txt
codigo,ENE,FEB,MAR,ABR,MAY,JUN,JUL,AGO,SEP,OCT,NOV,DIC 100034,32,12,45,67,84,114,21,57,99,84,74,65 201245,39,71,63,32,57,85,83,12,11,15,34,65 ...
El nombre del archivo debe ser el mismo de la categoría dentro del diccionario categorias y terminar con “.txt”.
Rúbrica: numeral 1.1 (8 puntos), numeral 1.2 (5 puntos),numeral 1.3 (8 puntos), numeral 1.4 (9 puntos), numeral 1.5 (6 puntos), numeral 1.6 (9 puntos), numeral 1.7 (15 puntos).
Referencia: Producción de brócoli crece 300% desde 2000
https://www.eluniverso.com/2005/03/24/0001/9/E2FB1BA3C6DC41C899E8B87A7F2FBD36.html
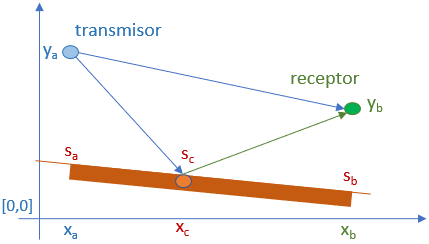
5.2 Optica – Rayo reflejado en plano inclinado con Python
Propagación multitrayecto o multicamino en plano inclinado
Referencia: Sears-Zemansky Cap33.2 Vol2 Ed.12 p1123, Optica – Rayo reflejado en plano horizontal
El plano de reflexión puede estar inclinado respecto al eje de las x. Para el caso dado, se puede considerar igualar las pendientes del rayo incidente y reflejado referenciadas con la pendiente del plano inclinado.
la pendiente del plano inclinado se obtiene como:
m_s = \frac{\Delta suelo } {\Delta x_{intervalo}} = \frac{s_b-s_a}{x_b-x_a}Respecto al plano, los ángulos de rayo incidente y reflejado son iguales por lo que secorrige con la pendiente del plano. Las pendientes del rayo izquierdo y rayo derecho con la influencia de la pendiente del suelo se igualan:
-(m_z-m_s) = m_r-m_s -m_z = m_r - 2 m_sPara obtener sc como un punto en el plano, requiere función de suelo(x) evaluada en sc , para usar todo en función de xc :
m_s = \frac{\Delta s}{\Delta x} = \frac{s_b-s_a}{x_b-x_a} s(x) = m_s x_a +b_s b_s = s_a-m_s x_a s_c = s(c) = m_s x_c +b_sLo anterior permite actualizar el planteamiento de la pendientes, y despejar el valor de la incógnita xc
-m_z = m_r - 2 m_s - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c}{x_b-x_c}-2m_s - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c-2m_s(x_b-x_c)}{x_b-x_c}primero se busca agrupar sc
-(x_b-x_c)(s_c-y_a) = (x_c-x_a)(y_b-s_c-2m_s(x_b-x_c))-s_c(x_b-x_c)+y_a(x_b-x_c) = y_b(x_c-x_a)-s_c(x_c-x_a)-2m_s(x_b-x_c)(x_c-x_a)
-s_c(x_b-x_c) + s_c(x_c-x_a) = -y_a(x_b-x_c) + y_b(x_c-x_a) - 2m_s(x_b-x_c)(x_c-x_a)
s_c(-x_b+x_c+x_c-x_a) = -x_b y_a+x_c y_a + y_b x_c - x_a y_b -2m_s(x_b(x_c-x_a)-x_c(x_c-x_a))
sutituyendo sc con la expresión del plano con pendiente evaluada en el punto xc , lo que se expresa como:
(m_s x_c +b_s)(2 x_c-(x_a+x_b)) = x_c (y_a + y_b)-(x_a y_b -x_b y_a)-2m_s(x_b x_c- x_a x_b - x_c^2 + x_a x_c))teniendo ahora como objetivo encontrar una expresión para xc
m_s x_c (2 x_c-(x_a+x_b))+b_s(2 x_c-(x_a+x_b)) = x_c (y_a + y_b)-(x_a y_b +x_b y_a)-2m_s(- x_c^2 + x_c(x_b + x_a) - x_a x_b)2m_s x_c^2 - m_s x_c(x_a+x_b)+2 b_s x_c-b_s(x_a+x_b) = x_c (y_a + y_b)-(x_a y_b +x_b y_a)+ 2m_s x_c^2 - 2m_s x_c (x_b + x_a) + 2m_s x_a x_b
x_c(- m_s (x_a+x_b)+2 b_s)-b_s(x_a+x_b) = x_c (y_a + y_b- 2m_s (x_b + x_a))-(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(- m_s (x_a+x_b)+2 b_s) -x_c (y_a + y_b- 2m_s (x_b + x_a)) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(2 b_s - (y_a + y_b) - m_s (x_a+x_b) + 2m_s (x_b + x_a)) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(2 b_s - (y_a + y_b) + m_s(x_a+x_b) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c(2 b_s - (y_a + y_b) + m_s (x_a+x_b)) = b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b
x_c = \frac{b_s(x_a+x_b) -(x_a y_b +x_b y_a) + 2m_s x_a x_b}{2 b_s - (y_a + y_b) + m_s (x_a+x_b)}
Con el valor de xc se pudede obtener la altura del punto sc. a partir de la ecuación que describe el plano s(x).
Algoritmo en Python
A partir del algoritmo del rayo reflejado en plano horizontal , se añaden las instrucciones para calcular ms, bs, xc, sc.
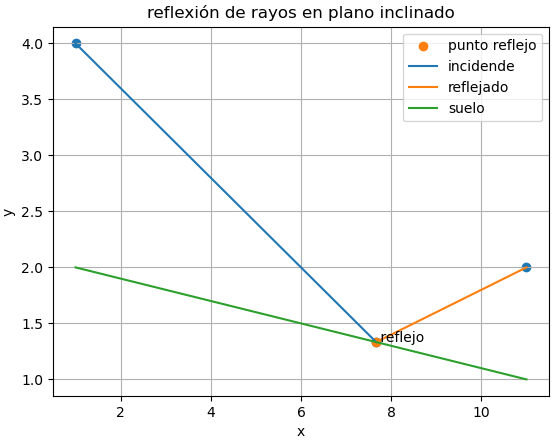
obteniendo ahora el resultado:
punto reflejado: [ 7.666666666666665 , 1.3333333333333335 ]
con la gráfica
Instrucciones en Python
# rayo incidente y reflejado # en plano inclinado # blog.espol.edu.ec/ccpg1001 import numpy as np import matplotlib.pyplot as plt # INGRESO # posición de antenas xa = 1 # Izquierda ya = 4 xb = 11 # Derecha yb = 2 # plano el suelo sa = 2 sb = 1 # muestras en grafica muestras = 21 # PROCEDIMIENTO # pendiente de suelo ms = (sb-sa)/(xb-xa) bs = sa-ms*xa # punto de reflejo numerador = bs*(xa+xb)-(xa*yb+xb*ya)+2*ms*xa*xb denominador = 2*bs-(ya+yb)+ms*(xa+xb) xc = numerador/denominador sc = ms*xc+bs # SALIDA print('punto reflejado: [',xc,',',sc,']') # GRAFICA #puntos en el plano plt.scatter([xa,xc,xb],[ya,sc,yb]) plt.scatter([xc],[sc],label='punto reflejo') # lineas de rayos plt.plot([xa,xc],[ya,sc],label='incidende') plt.plot([xc,xb],[sc,yb],label='reflejado') plt.plot([xa,xb],[sa,sb],label='suelo') # etiquetas anotadas plt.annotate(' reflejo',[xc,sc]) # etiquetas plt.legend() plt.xlabel('x') plt.ylabel('y') plt.title('reflexión de rayos en plano inclinado') plt.grid() plt.show()
Tarea: Consiere que el suelo está compuesto de al menos dos segmentos con inclinaciones diferentes. Podría darse mas de una reflexión al punto de recepción o ninguna
Una aplicación relacionada de análisis multitrayecto en Girni: Coordenadas – Rayo reflejado en perfil por tramos
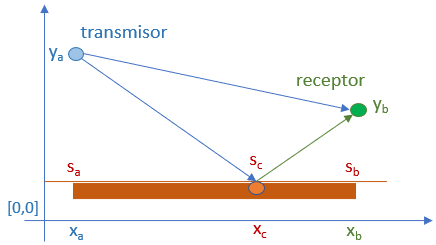
5.1 Optica – Rayo reflejado en plano horizontal con Python
Referencia: Sears-Zemansky Cap33.2 Vol2 Ed.12 p1123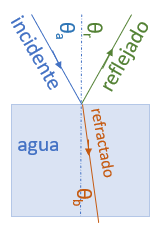
El modelo de luz basado en rayos permite describir la propagación por: reflexión y refracción.
Un rayo de onda luminosa que incide en una material liso que separa dos materiales transparentes (como el aire y el vidrio o el agua y el vidrio), el rayo es reflejado parcialmente y también refractado parcialmente hacia el segundo material.
Los rayos incidente, reflejado y refractado en una interfaz lisa entre dos materiales ópticos forman ángulos θa,θr,θb respecto a la normal (perpendicular) a la superficie en el punto de incidencia se ilustra en la figura. Si la superficie es rugosa, tanto la luz transmitida como la reflejada se dispersan en varias direcciones y no hay un ángulo único de transmisión o reflexión.
La reflexión con un ángulo definido desde una superficie muy lisa se llama reflexión especular ( latin de “espejo”). La reflexión dispersa a partir de una superficie áspera se llama reflexión difusa.
Propagación multitrayecto o multicamino en plano horizontal
Referencia: Propagación multicamino
En telecomunicaciones, la propagación de ondas de radio presentan un comportamiento semejante al de la luz para reflexión conocido como propagación multicamino o multitrayecto.
El fenómeno se da cuando las señales de radio llegan a la antena receptora por dos o más caminos y en diferentes tiempos.
La propagación mutitrayecto puede causar problemas en la recepción de la señal, debido a la interacción entre las señales recibidas. A fines prácticos, la señal obtenida en recepción difiere de la original y causa efectos que se han de compensar.
Ejercicio con gráfica
Realizar la gráfica de los rayos incidente, reflejado y directo entre el transmisor y receptor con antenas a diferentes alturas, semejante a la gráfica anterior.
 Desarrollo
Desarrollo
Si los ángulos incidente y reflejado son iguales, la pendiente rayo incidente debe ser igual en magnitud a la pendiente del rayo reflejado. Las pendientes tienen signo opuesto, el rayo izquierdo tiene pendiente negativa.
- \frac{\Delta y_{izquierda}} {\Delta x_{izquierda}} = \frac{\Delta y_{derecha}}{\Delta x_{derecha}} - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c}{x_b-x_c}Por facilidad de la ecuación, se supondrá que el suelo es paralelo al eje x, a una altura sc del eje de referencia.
Se debe obtener el valor de xc de la ecuación anterior, que realizando un poco de trabajo se obtiene que:
- (x_b-x_c)(s_c-y_a) = (x_c-x_a)(y_b-s_c) - x_b(s_c-y_a) + x_c (s_c-y_a) = x_c (y_b-s_c)-x_a (y_b-s_c) x_c (s_c-y_a) - x_c (y_b-s_c)= -x_a (y_b-s_c) + x_b(s_c-y_a) x_c (2s_c-y_a-y_b)= -x_a (y_b-s_c) + x_b(s_c-y_a) x_c = \frac{x_b(s_c-y_a)-x_a(y_b-s_c)}{2s_c-y_a-y_b}Obtenido el punto xc y dado que el plano es horizontal, la altura sc es constante.
Con el algoritmo se puede obtener el punto de reflexión para varias alturas de antena y varias alturas del plano.
resultado con datos muestra:
punto reflejado: [ 8.5 , 1 ]
Instrucciones en Python
# rayo incidente y reflejado # blog.espol.edu.ec/ccpg1001 import numpy as np import matplotlib.pyplot as plt # INGRESO # posición de antenas xa = 1 # Izquierda ya = 4 xb = 11 # Derecha yb = 2 # plano el suelo sc = 1 # altura # muestras en grafica muestras = 21 # PROCEDIMIENTO numerador = xb*(sc-ya)-xa*(yb-sc) denominador = 2*sc-ya-yb xc = numerador/denominador # SALIDA print('punto reflejado: [',xc,',',sc,']') # GRAFICA #puntos en el plano plt.scatter([xa,xc,xb],[ya,sc,yb]) plt.scatter([xc],[sc],label='punto reflejo') # lineas de rayos plt.plot([xa,xc],[ya,sc],label='incidende') plt.plot([xc,xb],[sc,yb],label='reflejado') plt.plot([xa,xb],[sc,sc],label='suelo') # etiquetas anotadas plt.annotate(' reflejo',[xc,sc]) # etiquetas plt.legend() plt.xlabel('x') plt.ylabel('y') plt.title('reflexión de rayos en plano') plt.grid() plt.show()
Tarea:
a) Añadir la trayectoria directa del rayo entre el transmisor y receptor
b) Considerar que el plano puede estar inclinado respecto al eje de las x,por lo que para igualar las pendientes del rayo incidente y reflejado se referencian con la pendiente del plano.
m_s = \frac{\Delta suelo } {\Delta x_{intervalo}} = \frac{s_b-s_a}{x_b-x_a} -(m_z-m_s) = m_r-m_s -m_z = m_r - 2 m_s