s1Eva_IIT2004_T3 Estimar π por Montecarlo

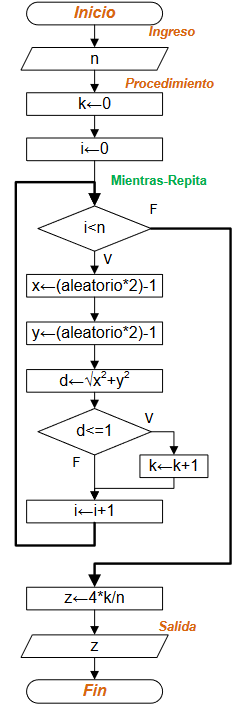
Ejercicio: 1Eva_IIT2004_T3 Estimar π por Montecarlo

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

Ingresar n como la cantidad de puntos en el plano a ubicar de forma aleatoria dentro del rango del cuadrado que inscribe al círculo.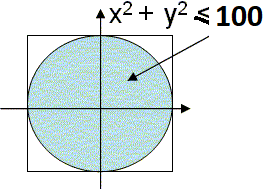

Usar una variable “k” como el contador para los puntos que caen dentro del círculo.

Al generar cada punto se puede calcular la distancia al centro mediante Pitágoras.

Se repite el proceso para n puntos y al final se calcula el valor estimado de pi acorde a la relación presentada.

Nota: no se usa como variable la palabra “pi” debido a que es nombre de variable reservada.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2004_T3 Estimar π por Montecarlo
# Propuesta de solución. edelros@espol.edu.ec
# Considera todo el circulo

import random as rnd
import numpy as np

# INGRESO
n = int(input('¿Cuántos puntos?: '))

# PROCEDIMIENTO
k = 0
i = 0
while (i<n):
    x = (rnd.random()*2)-1
    y = (rnd.random()*2)-1
    d = np.sqrt(x**2+y**2)
    if (d<=1):
        k = k+1
    i = i+1

z = 4*k/n

# SALIDA
print('Pi estimado es:')
print(z)

la estimación de π con números aleatorios que se ubican dentro del círculo de radio 1 es:

¿Cuántos puntos?: 1000
Pi estimado es:
3.196
>>> 
¿Cuántos puntos?: 1000
Pi estimado es:
3.188
>>>