1ra Evaluación I Término 2016-2017. Junio 28, 2016 /CCPG001 – FIEC
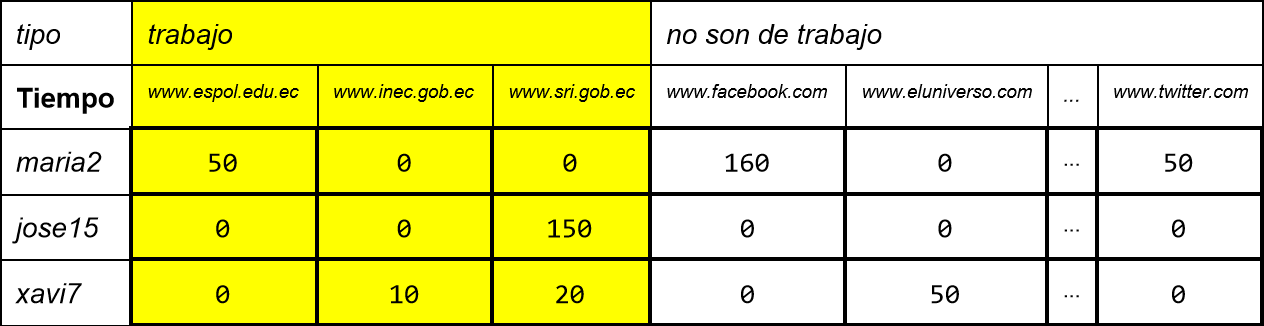
TEMA 3 . (40 puntos) Se dispone de un arreglo de NumPy que representa el tiempo[empleado, sitio] de navegación en Internet de una empresa expresada en un arreglo de nxm. El arreglo es similar al resultado del tema anterior, además también se dispone de las listas de los empleados y sitios de trabajo.
La empresa requiere elaborar un reporte de las visitas a internet que incluya los siguientes datos:
a. Tiempo total de uso de Internet.
b. Tiempo total de uso de Internet por empleado
c. Tiempo total de visita por sitio
d. Tiempo total de visita por sitio de trabajo
e. Tiempo total de visita por sitios que no son de trabajo
f. El nombre del empleado que más tiempo ha pasado en sitios que no son de trabajo
g. El sitio de trabajo que más tiempo ha sido usado
h. Si el proveedor de Internet cobra un valor de 5 centavos por minuto de visita alos sitios de trabajo y el doble para los otros sitios. Calcule el total a pagar en dólares.
i. ¿Cuántos empleados han visitado cada sitio ?
Desarrolle un programa en Python que calcule los resultados a las preguntas anteriores y muestre por pantalla las respuestas.
Referencia: Archivo original 1raEvaIT2016.pdf