arreglos-vectores – Página 7 – Fundamentos de Programación

2014-03-092023-02-04

1Eva_IT2009_T3 Plan de ahorro programado

1ra Evaluación I Término 2009 – 2010. Julio 07, 2009 /ICM00794

Tema 3 (25 puntos). Para usar un “Plan Acumulativo Mensual de Ahorro Programado” se han establecido las reglas que se muestran a continuación:

El depósito de ahorro mensual D es un valor fijo dado al inicio.
El valor meta P es dado inicialmente como un dato.
Los intereses ganados serán acumulados por mes, multiplicando el valor acumulado por 1% y agregándolo al valor acumulado actual.
Cada tres meses pueden hacerse retiros parciales con un valor R hasta 25% del valor total acumulado.
El valor total acumulado podrá retirarse sólo cuando se haya alcanzado el valor P

Realice un algoritmo que lea el valor del depósito mensual D y el valor P meta al cual se desea llegar.

Cada mes debe agregarse un valor D al monto acumulado,
Cada tres meses debe realizarse aleatoriamente un retiro con un valor aleatorio de hasta 25% del valor acumulado.

Determine:
¿cuántos meses y retiros se realizaron hasta alcanzar la meta P?

Rubrica: manejo de saldos (5 puntos), control de retiros (5 puntos), conteo de transacciones (5 puntos), solución estructurada (10 puntos).

2014-03-092024-01-12

1Eva_IIT2009_T3 Descomprimir arreglo

1ra Evaluación II Término 2009 – 2010. Diciembre 01, 2009 /ICM00794

Tema 3 (20 puntos). Al descomprimir datos (tema anterior) se restaura el arreglo original.

El método para descomprimir consiste en repetir el número de veces indicada por cada datoc en el arreglo de salida.

Realice un algoritmo para «descomprimir» los arreglos datoc y veces de tamaño n y presente el resultado como en el ejemplo.

Ejemplo:
j	1	2	3
datoc(j)	2	5	3
veces(j)	3	4	3

Se convierte en:
i	1	2	3	4	5	6	7	8	9	10
datos(i)	2	2	2	5	5	5	5	3	3	3

Nota: El proceso para comprimir se trata en el tema 2.

Rúbrica: Ingreso de datos comprimidos (5 puntos), repetir datos en el arreglo salida (10 puntos), muestra ordenada de datos (5 puntos)

Referencia: ¿Cómo demonios Funciona la COMPRESIÓN DE ARCHIVOS?. minuto 5:44 Tutos PC. 7 diciembre 2023

2014-03-092024-01-12

1Eva_IIT2009_T2 Comprimir arreglo

1ra Evaluación II Término 2009 – 2010. Diciembre 01, 2009 /ICM00794

Tema 2 (30 puntos). Al comprimir datos, el resultado tiene menor tamaño que el original.

Un método simple consiste en contar las repeticiones de consecutivas de cada dato para después almacenar solo el dato junto al número de veces que se repite.

Realice un algoritmo para «comprimir» un arreglo datos(i) con tamaño n que contiene números enteros y presente el resultado como en el ejemplo.

i	1	2	3	4	5	6	7	8	9	10
datos(i)	2	2	2	5	5	5	5	3	3	3

Se convierte en:
j	1	2	3
datoc(j)	2	5	3
veces(j)	3	4	3

Nota: El proceso para descomprimir se trata en el tema 3.

Rúbrica: conteo de números repetidos (10 puntos) arreglo de veces y datos (15 puntos), muestra ordenada de datos (5 puntos)

Referencia: ¿Cómo demonios Funciona la COMPRESIÓN DE ARCHIVOS?. minuto 5:44 Tutos PC. 7 diciembre 2023

2014-03-092023-02-04

1Eva_IIT2009_T1 Entrenamiento de atleta en pista circular

1ra Evaluación II Término 2009 – 2010. Diciembre 01, 2009 /ICM00794

Tema 1 (20 puntos). Para las Olimpiadas de Londres 2012 un atleta se prepara para competir en la maratón de 10 km entrenando en una pista circular de 1 km (perímetro).

En el entrenamiento, se registra el tiempo en segundos cada vez que pasa por la marca de inicio de pista (ej: 45,354 segundos).

Escriba un algoritmo que solicite al usuario y almacene el vector de tiempo en el que atleta pasó por la marca de inicio de pista en cada vuelta, luego determine y muestre las respuestas a las siguientes preguntas:

a) ¿Cuál fue la vuelta que se realizó en menor tiempo?
b) ¿Cuánto tiempo le tomo al atleta completar los 10 km?
c) ¿Cuánto es el tiempo promedio de las vueltas?

Rubrica: Manejo de vectores (5 puntos), vuelta menor tiempo (5 puntos), tiempo total (5 puntos), tiempo promedio por vuelta (5 puntos)

2014-03-082023-02-04

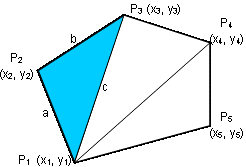1Eva_IIT2008_T4 Area del polígono convexo por triángulos

1ra Evaluación II Término 2008 – 2009. Diciembre 09, 2008 /ICM00794

Tema 4 (30 puntos). poligonoConvexo Escriba un algoritmo que permita leer las coordenadas (x, y) en el plano de un polígono convexo de n lados y calcule el área del polígono mediante la suma de las áreas de los triángulos que se forman con el vértice P₁.

Como ejemplo para un polígono de n=5 lados se muestra la figura.

Se dispone de las siguientes fórmulas: Área Triángulo A_{P1 P2 P3}

A_{P_1 P_2 P_3} = \sqrt{s(s-a)(s-b)(s-c)}

\text{Lado: } a = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}

de manera similar se calculan b y c, donde:

s = \frac{a+b+c}{2}

Rúbrica: Leer todas coordenadas para un arreglo (10 puntos), calcular el área de un polígono (10 puntos) Todas las áreas (10 puntos)

2014-03-082023-02-04

1Eva_IT2008_T4 Control de producción de plantas

1ra Evaluación I Término 2008 – 2009. Julio 08, 2008 /ICM00794

Tema 4 (30 puntos). Para evaluar un lote de producción de plantas se toma una muestra aleatoria correspondiente al 60% del total.

Si el 95% de plantas de dicha muestra cumple con las características especificadas, entonces se considera la muestra como un lote de calidad.

Una planta para ser considerada de calidad debe cumplir con una medida mínima de 22 cm, y vigor de 22 a 24 mm.

Escriba un algoritmo que almacene las características (medida y vigor) de n plantas en un vector (solicitadas al usuario), genere un vector en donde se indique si cada planta cumple las condiciones, seleccione una muestra aleatoria del 60% del número total de plantas, y verifique si el lote es de calidad.

i	medida (i)	vigor (i)	muestreo (i)
1	19	22	0
2	23	23	1
3	25	24	1
4	18	17	0
5	21	22	0
6	22	19	0
7	25	23	1
8	24	21	0
…
n	24	21	0

Cumplimiento: 97%, Lote de calidad: SI

2014-03-082023-02-04

1Eva_IIT2008_T3 Tiempos de recorrido en metrovia

1ra Evaluación II Término 2008 – 2009. Diciembre 09, 2008 /ICM00794

Tema 3 (25 puntos). Del recorrido completo de un bus de metrovía se registran las horas de partida de las n estaciones por las que pasa.

Realice un algoritmo para:
a) Registrar la hora y minuto de partida en cada estación (5 puntos),
b) Determinar el tramo recorrido de mayor duración (15 puntos) y,
c) Calcular la duración de todo el recorrido (5 puntos).

Ejemplo para n=3 estaciones:
Estación	Hora	Minuto	Tiempo
1	6	30	0
2	7	12	42
3	8	43	91

Tramo mayor duración: 2 a 3
Total Tiempo Recorrido: 2 horas y 13 min.

Sugerencia: convierta a minutos todos los registros para determinar la diferencia.

2014-03-082023-02-04

1Eva_IT2008_T3 Simular precio de petroleo

1ra Evaluación I Término 2008 – 2009. Julio 08, 2008 /ICM00794

Tema 3 (30 puntos). Se ha realizado un muestreo con los precios del barril de petróleo durante el último mes (de 30 días), suponga que dichos valores son enteros y que han fluctuado entre $ 130 y $ 150 (en forma aleatoria). prpetroleo

Una vez elaborada la muestra, se desea determinar:

a) El promedio del precio del petróleo

b) ¿Cuál fue el día en el que estuvo más barato el barril de petróleo?

c) ¿Cuántos días el petróleo tuvo precios superiores al promedio?

2014-03-082023-02-04

1Eva_IIT2008_T2 Sortear jueces para salas CNJ

1ra Evaluación II Término 2008 – 2009. Diciembre 09, 2008 /ICM00794

Tema 2 (25 puntos). En el proceso de transición institucional que establece la nueva Constitución, aprobada en el referendo del pasado 28 de septiembre del 2008, la principal entidad jurisdiccional será la Corte Nacional de Justicia (CNJ). (www.eluniverso.com 25/octubre/2008)

La CNJ estará conformada por 21 de 31 jueces que integraron la anterior Corte Suprema de Justicia (CSJ) y escogidos mediante sorteo público.

Realice un algoritmo que permita realizar el sorteo público de n entre m jueces de la CSJ (15 puntos) y los muestre en forma ordenada (10 puntos).

Nota.- Cada juez se representa por un número, en el sorteo no deben repetirse los jueces escogidos

2014-03-082023-02-04

1Eva_IT2008_T2 Criba de Eratóstenes con Python

1ra Evaluación I Término 2008 – 2009. Julio 08, 2008 /ICM00794

Tema 2 (20 puntos). Una forma de hallar todos los números primos menores que un número natural n, es el método de la “Criba de Eratóstenes” que consiste en lo siguiente:

Ejemplo: Para n=20 Se forma un vector con todos los números naturales entre 2 y n. Se tachan todos los múltiplos de 2 que son menores que n, luego se tachan los múltiplos de 3 que son menores que n, y así sucesivamente. El procedimiento se repite hasta alcanzar todos los múltiplos de los números naturales menores que n. Los números no tachados corresponden a los números primos. Primos: 2, 3, 5, 7, 11, 13, 17, 19 Elabore un algoritmo que, dado un número entero positivo n mayor que 1, muestre los números primos encontrados con el método descrito.	i	criba[i]
	2	1
	3	1
	4	0
	5	1
	6	0
	7	1
	8	0
	9	0
	10	0
	11	1
	12	0
	13	1
	14	0
	15	0
	16	0
	17	1
	18	0
	19	1
	20	0