1ra Evaluación II Término 2012-2013. Noviembre 27, 2012 /ICM00794
Tema 3 (30 puntos) El juego “Hundir el Barco Enemigo” consiste en realizar disparos desde un cañón defensor para hundir un barco rival mientras éste intenta esquivarse.
Considere en un plano cartesiano con las posiciones de ambos.
El cañón permanece en su ubicación inicial, mientras que el barco rival para evadir el disparo puede desplazarse aleatoriamente x metros (entre 1 y 3) y en una dirección aleatoria hacia el norte, sur, este u oeste.
Elabore un algoritmo que permita ingresar la ubicación inicial de avistamiento del barco rival (bx,by), luego registre la ubicación a donde el cañón dispara (cx,cy).
Simule el movimiento de evasión del barco y disparo del cañón, para luego verificar si se alcanzó el objetivo de “Hundir el Barco Enemigo”.
El juego se repite para n intentos de disparo y evasión, al final muestre el resultado del juego.
| eje y |
5 |
|
|
|
 |
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
 |
1 |
2 |
3 |
4 |
5 |
eje x |
¿Cuántas municiones? 3
Barco ¿Coordenada bx?: 5
Barco ¿Coordenada by?: 4
Intento 1
Disparo ¿Coordenada cx?: 5
Disparo ¿Coordenada cy?: 3
Movimiento: Sur , 2 casillas
Disparados: 1
Hundido: 0
Intento 2
…
Rúbrica: Ingreso de Coordenadas (5 puntos), control de disparos (5 puntos), simulación de evasión (5 puntos), verificar hundimiento (5 puntos). Resultados finales (5 puntos), Algoritmo integrado y estructurado (5 puntos).
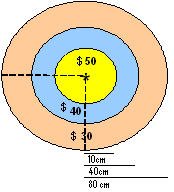
 que reciba una cantidad de dólares (número entero) y encuentre su equivalente, usando la menor cantidad de billetes de 50, 20, 10, 5, 1, entregando el resultado en un vector.
que reciba una cantidad de dólares (número entero) y encuentre su equivalente, usando la menor cantidad de billetes de 50, 20, 10, 5, 1, entregando el resultado en un vector.