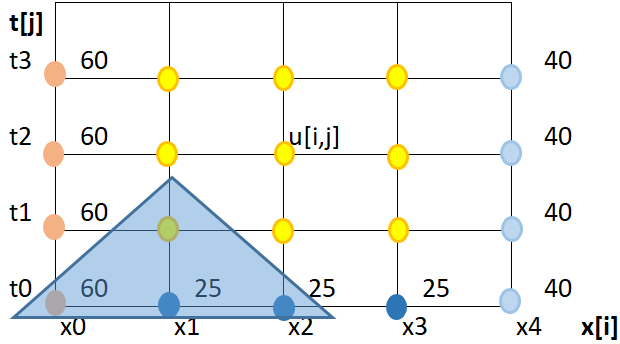
con el resultado desarrollado en EDP elípticas para:

\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{ \partial y^2} = 0

y con el supuesto que: \lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = 1

se puede plantear que:

u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} = 0

que reordenando para un punto central desconocido se convierte a:

u_{i,j} = \frac{1}{4} \big[ u_{i+1,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} \big]

con lo que se interpreta que cada punto central es el resultado del promedio de los puntos alrededor del rombo formado en la malla.

El cálculo numerico se puede realizar de forma iterativa haciendo varias pasadas en la matriz, promediando cada punto. Para revisar las iteraciones se controla la convergencia junto con un máximo de iteraciones.

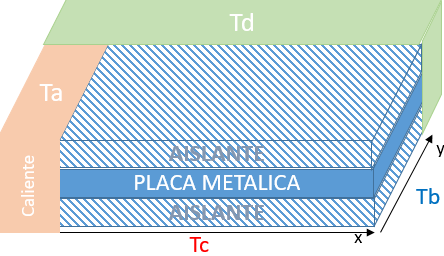
# Ecuaciones Diferenciales Parciales
# Elipticas. Método iterativo
import numpy as np

# INGRESO
# Condiciones iniciales en los bordes
Ta = 60
Tb = 60
Tc = 50
Td = 70
# dimensiones de la placa
x0 = 0
xn = 2
y0 = 0
yn = 1.5
# discretiza, supone dx=dy
dx = 0.25 
dy = 0.25 
maxitera = 100
tolera = 0.0001

# PROCEDIMIENTO
xi = np.arange(x0,xn+dx,dx)
yj = np.arange(y0,yn+dy,dy)
n = len(xi)
m = len(yj)
# Matriz u
u = np.zeros(shape=(n,m),dtype = float)
# valores en fronteras
u[0,:]   = Ta
u[n-1,:] = Tb
u[:,0]   = Tc
u[:,m-1] = Td

# valor inicial de iteración
promedio = (Ta+Tb+Tc+Td)/4
u[1:n-1,1:m-1] = promedio
# iterar puntos interiores
itera = 0
converge = 0
while not(itera>=maxitera or converge==1):
    itera = itera +1
    nueva = np.copy(u)
    for i in range(1,n-1):
        for j in range(1,m-1):
            u[i,j] = (u[i-1,j]+u[i+1,j]+u[i,j-1]+u[i,j+1])/4
    diferencia = nueva-u
    erroru = np.linalg.norm(np.abs(diferencia))
    if (erroru<tolera):
        converge = 1

# SALIDA
np.set_printoptions(precision=2)
print('converge = ', converge)
print('xi=')
print(xi)
print('yj=')
print(yj)
print('matriz u')
print(u)

Un ejemplo de resultados:

converge = 1
xi=
[ 0.    0.25  0.5   0.75  1.    1.25  1.5   1.75  2.  ]
yi=
[ 0.    0.25  0.5   0.75  1.    1.25  1.5 ]
matriz u
[[ 50.    60.    60.    60.    60.    60.    70.  ]
 [ 50.    55.6   58.23  60.    61.77  64.4   70.  ]
 [ 50.    54.15  57.34  60.    62.66  65.85  70.  ]
 [ 50.    53.67  56.97  60.    63.03  66.33  70.  ]
 [ 50.    53.55  56.87  60.    63.13  66.45  70.  ]
 [ 50.    53.67  56.97  60.    63.03  66.33  70.  ]
 [ 50.    54.15  57.34  60.    62.66  65.85  70.  ]
 [ 50.    55.6   58.23  60.    61.77  64.4   70.  ]
 [ 50.    60.    60.    60.    60.    60.    70.  ]]
>>>

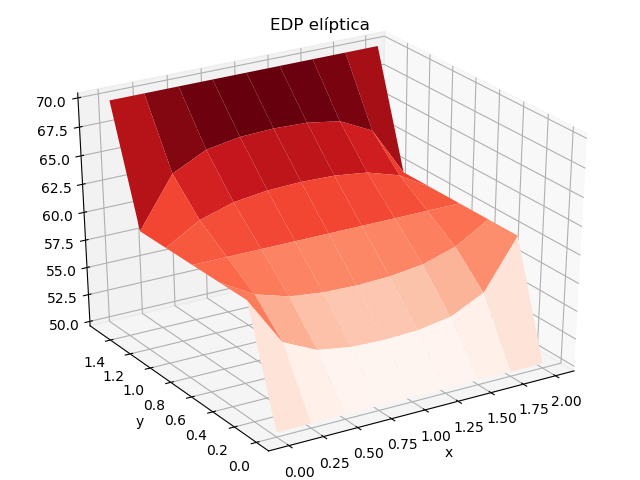
Cuyos valores se interpretan mejor en una gráfica, en este caso 3D:

La gráfica de resultados requiere ajuste de ejes, pues el índice de filas es el eje x, y las columnas es el eje y. La matriz graficada se obtiene como la transpuesta de u

# Gráfica
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

X, Y = np.meshgrid(xi, yj)
U = np.transpose(u) # ajuste de índices fila es x

figura = plt.figure()
ax = Axes3D(figura)
ax.plot_surface(X, Y, U,
                rstride=1,
                cstride=1,
                cmap=cm.Reds)

plt.title('EDP elíptica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Referencia:  Chapra 30.3 p893 pdf917, Burden 9Ed 12.2 p729, Rodriguez 10.2.4 p415

Se utiliza el mismo ejercicio presentado en método explícito.

\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}

En éste caso se usan diferencias finitas centradas y hacia atras; la línea de referencia es t₁:

\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} \frac{\partial u}{\partial t} = \frac{u_{i,j} - u_{i,j-1} }{\Delta t}

La selección de las diferencias divididas corresponden a los puntos que se quieren usar para el cálculo, se observan mejor en la gráfica de la malla.

Luego se sustituyen en la ecuación del problema, obteniendo:

\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j}-u_{i,j-1}}{\Delta t}

De la gráfica se destaca que en la fórmula, dentro del triángulo solo hay DOS valores desconocidos, destacados por los punto en amarillo.
En la ecuación se representa por U[i,j] y U[i+1,j]. Por lo que será necesario crear un sistema de ecuaciones sobre toda la línea de tiempo t₁ para resolver el problema.

Despejando la ecuación, se agrupan términos constantes: λ = \frac{\Delta t}{K (\Delta x)^2} .

\lambda u_{i-1,j} + (-1-2\lambda) u_{i,j} + \lambda u_{i+1,j} = -u_{i,j-1}

Los parámetro P, Q y R se determinan de forma semejante al método explícito:

P = \lambda Q = -1-2\lambda R = \lambda Pu_{i-1,j} + Qu_{i,j} + Ru_{i+1,j} = -u_{i,j-1}

Los valores en los extremos son conocidos, para los puntos intermedios  se crea un sistema de ecuaciones para luego usar la forma Ax=B y resolver los valores para cada u(x_i,t_j).

Por ejemplo con cuatro tramos entre extremos se tiene que:
indice de tiempo es 1 e índice de x es 1.

i=1,j=1

Pu_{0,1} + Qu_{1,1} + Ru_{2,1} = -u_{1,0}

i=2,j=1

Pu_{1,1} + Qu_{2,1} + Ru_{3,1} = -u_{2,0}

i=3,j=1

Pu_{2,1} + Qu_{3,1} + Ru_{4,1} = -u_{3,0}

agrupando ecuaciones y sustituyendo valores conocidos:
\begin{cases} Qu_{1,1} + Ru_{2,1} + 0 &= -T_{0}-PT_{A}\\Pu_{1,1} + Qu_{2,1} + Ru_{3,1} &= -T_{0}\\0+Pu_{2,1}+Qu_{3,1}&=-T_{0}-RT_{B}\end{cases}

que genera la matriz a resolver:

\begin{bmatrix} Q && R && 0 && -T_{0}-PT_{A}\\P && Q && R && -T_{0}\\0 && P && Q && -T_{0}-RT_{B}\end{bmatrix}

Use alguno de los métodos de la unidad 3 para resolver el sistema y obtener los valores correspondientes.

Por la extensión de la solución es conveniente usar un algoritmo y convertir los pasos o partes pertinentes a funciones.

Tarea: Revisar y comparar con el método explícito.

---

Algoritmos en Python

para la solución con el método implícito.

# EDP parabólicas d2u/dx2  = K du/dt
# método implícito
# Referencia: Chapra 30.3 p.895 pdf.917
#       Rodriguez 10.2.5 p.417
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# Valores de frontera
Ta = 60
Tb = 40
T0 = 25
# longitud en x
a = 0
b = 1
# Constante K
K = 4
# Tamaño de paso
dx = 0.1
dt = 0.01
# iteraciones en tiempo
n = 100

# PROCEDIMIENTO
# Valores de x
xi = np.arange(a,b+dx,dx)
m  = len(xi)
ultimox = m-1

# Resultados en tabla de u
u = np.zeros(shape=(m,n), dtype=float)
# valores iniciales de u[:,j]
j = 0
ultimot = n-1
u[0,j]= Ta
u[1:ultimox,j] = T0
u[ultimox,j] = Tb

# factores P,Q,R
lamb = dt/(K*dx**2)
P = lamb
Q = -1 -2*lamb
R = lamb

# Calcula U para cada tiempo + dt
j = 1
while not(j>=n):
    u[0,j] = Ta
    u[m-1,j] = Tb

    # Matriz de ecuaciones
    tamano = m-2
    A = np.zeros(shape=(tamano,tamano), dtype = float)
    B = np.zeros(tamano, dtype = float)
    for f in range(0,tamano,1):
        if (f>0):
            A[f,f-1]=P
        A[f,f] = Q
        if (f<(tamano-1)):
            A[f,f+1]=R
        B[f] = -u[f+1,j-1]
    B[0] = B[0]-P*u[0,j]
    B[tamano-1] = B[tamano-1]-R*u[m-1,j]
    # Resuelve sistema de ecuaciones
    C = np.linalg.solve(A, B)
    
    # copia resultados a u[i,j]
    for f in range(0,tamano,1):
        u[f+1,j] = C[f]

    # siguiente iteración
    j = j + 1
        
# SALIDA
print('Tabla de resultados')
np.set_printoptions(precision=2)
print(u)

algunos valores:

Tabla de resultados
[[ 60.    60.    60.   ...,  60.    60.    60.  ]
 [ 25.    31.01  35.25 ...,  57.06  57.09  57.11]
 [ 25.    26.03  27.49 ...,  54.22  54.26  54.31]
 ..., 
 [ 25.    25.44  26.07 ...,  42.22  42.27  42.31]
 [ 25.    27.57  29.39 ...,  41.07  41.09  41.11]
 [ 40.    40.    40.   ...,  40.    40.    40.  ]]

Para realizar la gráfica se aplica lo mismo que en el método explícito

# Gráfica
salto = int(n/10)
if (salto == 0):
    salto = 1
for j in range(0,n,salto):
    vector = u[:,j]
    plt.plot(xi,vector)
    plt.plot(xi,vector, '.m')

plt.xlabel('x[i]')
plt.ylabel('t[j]')
plt.title('Solución EDP parabólica')
plt.show()

Queda por revisar la convergencia y estabilidad de la solución a partir de los O(h) de cada aproximación usada. Revisar los criterios en Chapra 30.2.1 p891 pdf915, Burden 9Ed 12.2 p727, Rodriguez 10.2.2 pdf409 .

Tarea o proyecto: Realizar la comparación de tiempos de ejecución entre los métodos explícitos e implícitos. La parte de animación funciona igual en ambos métodos.

Los tiempos de ejecución se determinan usando:

http://blog.espol.edu.ec/analisisnumerico/recursos/resumen-python/tiempos-de-ejecucion/

Referencia:  Chapra 30.2 p888 pdf912, Burden 9Ed 12.2 p725, Rodriguez 10.2 p406

Siguiendo el tema anterior en 9.1, se tiene que:

\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}

Se usan las diferencias divididas, donde se requieren dos valores para la derivada de orden uno y tres valores para la derivada de orden dos:

\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} \frac{\partial u}{\partial t} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t}

La selección de las diferencias divididas corresponden a los puntos que se quieren usar para el cálculo, se observan mejor en la gráfica de la malla. La línea de referencia es el tiempo t₀

Luego se sustituyen en la ecuación del problema, obteniendo:

\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j+1}-u_{i,j}}{\Delta t}

De la gráfica se destaca que en la fórmula solo hay un valor desconocido, destacado por el punto en amarillo dentro del triángulo. En la ecuación se representa por U[i,j+1].

Despejando la ecuación, se agrupan términos constantes:

λ = \frac{\Delta t}{K (\Delta x)^2}

quedando la ecuación, con los términos ordenados de izquierda a derecha como en la gráfica:

u_{i,j+1} = \lambda u_{i-1,j} +(1-2\lambda)u_{i,j}+\lambda u_{i+1,j}

Al resolver se encuentra que que cada valor en un punto amarillo se calcula como una suma ponderada de valores conocidos, por lo que el desarrollo se conoce como el método explícito.

La ponderación está determinada por los términos P, Q, y R.

\lambda = \frac{\Delta t}{K(\Delta x)^2} P = \lambda Q = 1-2\lambda R = \lambda u_{i ,j+1} = Pu_{i-1,j} + Qu_{i,j} + Ru_{i+1,j}

Fórmulas que se desarrollan usando un algoritmo y considerando que al disminuir los valores de Δx y Δt la cantidad de operaciones aumenta.

Queda por revisar la convergencia y estabilidad de la solución a partir de los O(h) de cada aproximación usada.

Revisar los criterios en:  Chapra 30.2.1 p891 pdf915, Burden 9Ed 12.2 p727, Rodriguez 10.2.2 pdf409 .

\lambda \leq \frac{1}{2}

Cuando λ ≤ 1/2 se tiene como resultado una solución donde los errores no crecen, sino que oscilan.
Haciendo λ ≤ 1/4 asegura que la solución no oscilará.
También se sabe que con λ= 1/6 se tiende a minimizar los errores por truncamiento (véase Carnahan y cols., 1969).

Para resolver la parte numérica suponga:

Valores de frontera: Ta = 60, Tb = 40, T0 = 25 
Longitud en x a = 0, b = 1 
Constante K= 4 
Tamaño de paso dx = 0.1, dt = dx/10

 

---

Algoritmo en Python

Se presenta la propuesta en algoritmo para el método explícito.

# EDP parabólicas d2u/dx2  = K du/dt
# método explícito,usando diferencias divididas
# Referencia: Chapra 30.2 p.888 pdf.912
#       Rodriguez 10.2 p.406
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# Valores de frontera
Ta = 60
Tb = 40
T0 = 25
# longitud en x
a = 0
b = 1
# Constante K
K = 4
# Tamaño de paso
dx = 0.1
dt = dx/10
# iteraciones en tiempo
n = 200

# PROCEDIMIENTO
# iteraciones en longitud
xi = np.arange(a,b+dx,dx)
m = len(xi)
ultimox = m-1

# Resultados en tabla u[x,t]
u = np.zeros(shape=(m,n), dtype=float)

# valores iniciales de u[:,j]
j=0
ultimot = n-1
u[0,:]= Ta
u[1:ultimox,j] = T0
u[ultimox,:] = Tb

# factores P,Q,R
lamb = dt/(K*dx**2)
P = lamb
Q = 1 - 2*lamb
R = lamb

# Calcula U para cada tiempo + dt
j = 0
while not(j>=ultimot): # igual con lazo for
    for i in range(1,ultimox,1):
        u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j]
    j=j+1

# SALIDA
print('Tabla de resultados')
np.set_printoptions(precision=2)
print(u)

Se muestra una tabla resumida de resultados a forma de ejemplo.

Tabla de resultados
[[ 60.    60.    60.   ...,  60.    60.    60.  ]
 [ 25.    33.75  38.12 ...,  57.93  57.93  57.93]
 [ 25.    25.    27.19 ...,  55.86  55.86  55.87]
 ..., 
 [ 25.    25.    25.94 ...,  43.86  43.86  43.87]
 [ 25.    28.75  30.62 ...,  41.93  41.93  41.93]
 [ 40.    40.    40.   ...,  40.    40.    40.  ]]
>>> 

Si la cantidad de puntos aumenta al disminuir Δx y Δt, es mejor disminuir la cantidad de curvas a usar en el gráfico para evitar superponerlas. Se usa el parámetro ‘salto’ para indicar cada cuántas curvas calculadas se incorporan en la gráfica.

# Gráfica
salto = int(n/10)
if (salto == 0):
    salto = 1
for j in range(0,n,salto):
    vector = u[:,j]
    plt.plot(xi,vector)
    plt.plot(xi,vector, '.r')
    
plt.xlabel('x[i]')
plt.ylabel('t[j]')
plt.title('Solución EDP parabólica')
plt.show()

Note que en la gráfica se toma como coordenadas x vs t, mientras que para la solución de la malla en la matriz las se usan filas y columnas. En la matriz el primer índice es fila y el segúndo índice es columna.

Tarea o Proyecto: Realizar la animación de los cambios de temperatura en el tiempo.