Referencia: Chapra 29.1 p866 pdf890, Rodriguez 10.3 p425, Burden 12.1 p694 pdf704
Las Ecuaciones Diferenciales Parciales tipo elípticas semejantes a la mostrada:
\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{ \partial y^2} = 0(ecuación de Laplace, Ecuación de Poisson con f(x,y)=0)
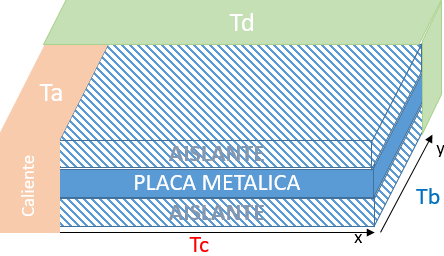
se interpreta como una placa metálica de dimensiones Lx y Ly, delgada con aislante que recubren las caras de la placa, y sometidas a condiciones en las fronteras:
Lx = dimensión x de placa metálica Ly = dimensión y de placa metálica u[0,y] = Ta u[Lx,y] = Tb u[x,0] = Tc u[x,Ly] = Td
Para el planteamiento se usa una malla en la que cada nodo corresponden a los valores u[xi,yj]. Para simplificar la nomenclatura se usan los subíndices i para el eje de las x y j para el eje t, quedando u[i,j].
Se discretiza la ecuación usando diferencias divididas que se sustituyen en la ecuación, por ejemplo:
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} + \frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{(\Delta y)^2}=0Se agrupan los términos de los diferenciales:
\frac{(\Delta y)^2}{(\Delta x)^2} \Big( u_{i+1,j}-2u_{i,j} +u_{i-1,j} \Big)+ u_{i,j+1}-2u_{i,j}+u_{i,j-1}=0con lo que se simplifican los valores como uno solo \lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = 1 . Por facilidad de lo que se realiza se supone que lambda tiene valor de 1 o los delta son iguales.
u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} = 0Obteniendo así la solución numérica conceptual. La forma de resolver el problema determina el nombre del método a seguir.