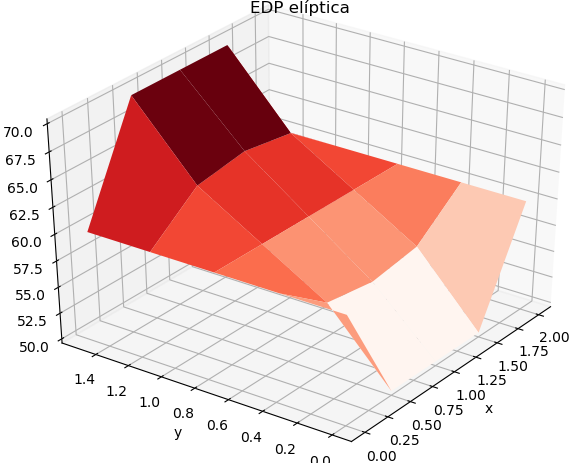
Publicado en por Edison Del Rosario

7.2.2 EDP Elípticas método implícito

con el resultado desarrollado en EDP elípticas para:

\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{ \partial y^2} = 0

y con el supuesto que: \lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = 1

se puede plantear que:

u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} = 0

con lo que para el método implícito, se plantea un sistema de ecuaciones para determinar los valores en cada punto desconocido.

j=1, i =1

u_{2,1}-4u_{1,1}+u_{0,1} + u_{1,2} +u_{1,0} = 0 u_{2,1}-4u_{1,1}+Ta + u_{1,2} +Tc= 0 -4u_{1,1}+u_{2,1}+u_{1,2} = -(Tc+Ta)

j=1, i =2

u_{3,1}-4u_{2,1}+u_{1,1} + u_{2,2} +u_{2,0} = 0 u_{3,1}-4u_{2,1}+u_{1,1} + u_{2,2} +Tc = 0 u_{1,1}-4u_{2,1}+u_{3,1}+ u_{2,2}= -Tc

j=1, i=3

u_{4,1}-4u_{3,1}+u_{2,1} + u_{3,2} +u_{3,0} = 0 Tb-4u_{3,1}+u_{2,1} + u_{3,2} +Tc = 0 u_{2,1} -4u_{3,1} + u_{3,2} = -(Tc+Tb)

j=2, i=1

u_{2,2}-4u_{1,2}+u_{0,2} + u_{1,3} +u_{1,1} = 0 u_{2,2}-4u_{1,2}+Ta + u_{1,3} +u_{1,1} = 0 -4u_{1,2}+u_{2,2}+u_{1,1}+u_{1,3} = -Ta

j = 2, i = 2

u_{1,2}-4u_{2,2}+u_{3,2} + u_{2,3} +u_{2,1} = 0

j = 2, i = 3

u_{4,2}-4u_{3,2}+u_{2,2} + u_{3,3} +u_{3,1} = 0 Tb-4u_{3,2}+u_{2,2} + u_{3,3} +u_{3,1} = 0 u_{2,2} -4u_{3,2}+ u_{3,3} +u_{3,1} = -Tb

j=3, i = 1

u_{2,3}-4u_{1,3}+u_{0,3} + u_{1,4} +u_{1,2} = 0 u_{2,3}-4u_{1,3}+Ta + Td +u_{1,2} = 0 -4u_{1,3}+u_{2,3}+u_{1,2} = -(Td+Ta)

j=3, i = 2

u_{3,3}-4u_{2,3}+u_{1,3} + u_{2,4} +u_{2,2} = 0 u_{3,3}-4u_{2,3}+u_{1,3} + Td +u_{2,2} = 0 +u_{1,3} -4u_{2,3}+u_{3,3} +u_{2,2} = -Td

j=3, i=3

u_{4,3}-4u_{3,3}+u_{2,3} + u_{3,4} +u_{3,2} = 0 Tb-4u_{3,3}+u_{2,3} + Td +u_{3,2} = 0 u_{2,3}-4u_{3,3}+u_{3,2} = -(Td+Tb)

con las ecuaciones se arma una matriz:

A = np.array([
    [-4, 1, 0, 1, 0, 0, 0, 0, 0],
    [ 1,-4, 1, 0, 1, 0, 0, 0, 0],
    [ 0, 1,-4, 0, 0, 1, 0, 0, 0],
    [ 1, 0, 0,-4, 1, 0, 1, 0, 0],
    [ 0, 1, 0, 1,-4, 1, 0, 1, 0],
    [ 0, 0, 1, 0, 1,-4, 0, 0, 1],
    [ 0, 0, 0, 1, 0, 0,-4, 1, 0],
    [ 0, 0, 0, 0, 1, 0, 1,-4, 1],
    [ 0, 0, 0, 0, 0, 1, 0, 1,-4],
    ])
B = np.array([-(Tc+Ta),-Tc,-(Tc+Tb),
                  -Ta,   0,    -Tb,
              -(Td+Ta),-Td,-(Td+Tb)])

que al resolver el sistema de ecuaciones se obtiene:

>>> Xu
array([ 56.43,  55.71,  56.43,  60.  ,  60.  ,  60.  ,  63.57,  64.29,
        63.57])

ingresando los resultados a la matriz u:

xi=
[ 0.   0.5  1.   1.5  2. ]
yj=
[ 0.    0.38  0.75  1.12  1.5 ]
matriz u
[[ 60.    60.    60.    60.    60.  ]
 [ 50.    56.43  60.    63.57  70.  ]
 [ 50.    55.71  60.    64.29  70.  ]
 [ 50.    56.43  60.    63.57  70.  ]
 [ 60.    60.    60.    60.    60.  ]]
>>>

Algoritmo usado para resolver el problema:

# Ecuaciones Diferenciales Parciales
# Elipticas. Método implícito
import numpy as np

# INGRESO
# Condiciones iniciales en los bordes
Ta = 60
Tb = 60
Tc = 50
Td = 70
# dimensiones de la placa
x0 = 0
xn = 2
y0 = 0
yn = 1.5
# discretiza, supone dx=dy
tramosx = 4
tramosy = 4
dx = (xn-x0)/tramosx 
dy = (yn-y0)/tramosy 
maxitera = 100
tolera = 0.0001

A = np.array([
    [-4, 1, 0, 1, 0, 0, 0, 0, 0],
    [ 1,-4, 1, 0, 1, 0, 0, 0, 0],
    [ 0, 1,-4, 0, 0, 1, 0, 0, 0],
    [ 1, 0, 0,-4, 1, 0, 1, 0, 0],
    [ 0, 1, 0, 1,-4, 1, 0, 1, 0],
    [ 0, 0, 1, 0, 1,-4, 0, 0, 1],
    [ 0, 0, 0, 1, 0, 0,-4, 1, 0],
    [ 0, 0, 0, 0, 1, 0, 1,-4, 1],
    [ 0, 0, 0, 0, 0, 1, 0, 1,-4],
    ])
B = np.array([-(Tc+Ta),-Tc,-(Tc+Tb),
              -Ta,0,-Tb,
              -(Td+Ta),-Td,-(Td+Tb)])


# PROCEDIMIENTO
# Resuelve sistema ecuaciones
Xu = np.linalg.solve(A,B)
[nx,mx] = np.shape(A)

xi = np.arange(x0,xn+dx,dx)
yj = np.arange(y0,yn+dy,dy)
n = len(xi)
m = len(yj)

u = np.zeros(shape=(n,m),dtype=float)
u[:,0]   = Tc
u[:,m-1] = Td
u[0,:]   = Ta
u[n-1,:] = Tb
u[1:1+3,1] = Xu[0:0+3]
u[1:1+3,2] = Xu[3:3+3]
u[1:1+3,3] = Xu[6:6+3]

# SALIDA
np.set_printoptions(precision=2)
print('xi=')
print(xi)
print('yj=')
print(yj)
print('matriz u')
print(u)

La gráfica de resultados se obtiene de forma semejante al ejercicio con método iterativo.

# Gráfica
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

X, Y = np.meshgrid(xi, yj)
U = np.transpose(u) # ajuste de índices fila es x

figura = plt.figure()
ax = Axes3D(figura)
ax.plot_surface(X, Y, U, rstride=1, cstride=1, cmap=cm.Reds)

plt.title('EDP elíptica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Se podría estandarizar un poco más el proceso para que sea realizado por el algoritmo y sea más sencillo generar la matriz con más puntos. Tarea.