Etiqueta: algoritmo Python

Referencia:  Chapra PT8.1 p.860 pdf.884,  Rodriguez 10.4 p.435

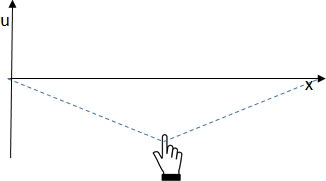
Las Ecuaciones Diferenciales Parciales tipo hiperbólicas semejantes a la mostrada, para un ejemplo en particular, representa la ecuación de onda de una dimensión u[x,t], que representa el desplazamiento vertical de una cuerda.

\frac{\partial ^2 u}{\partial t^2}=c^2\frac{\partial ^2 u}{\partial x^2}

Los extremos de la cuerda de longitud unitaria están sujetos y referenciados a una posición 0 a la izquierda y 1 a la derecha.

u[x,t] , 0<x<1, t≥0
u(0,t) = 0 , t≥0
u(1,t) = 0 , t≥0

Al inicio, la cuerda está estirada por su punto central:

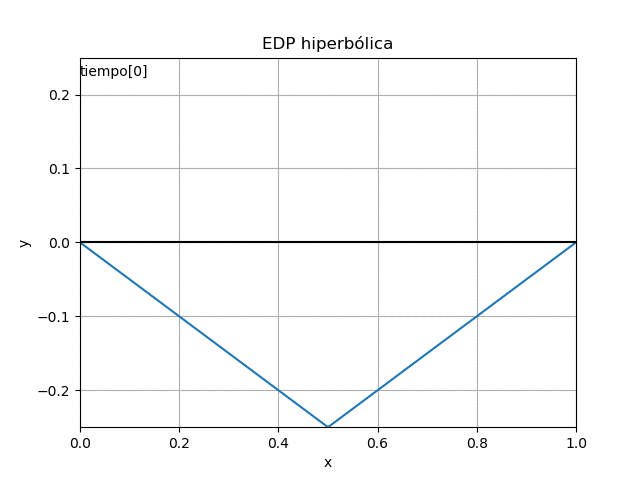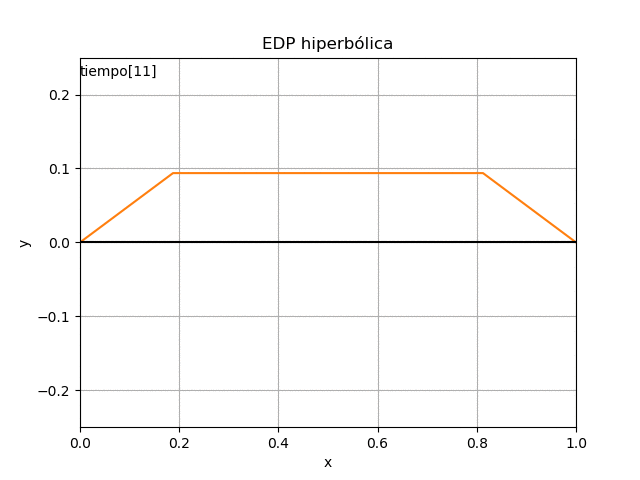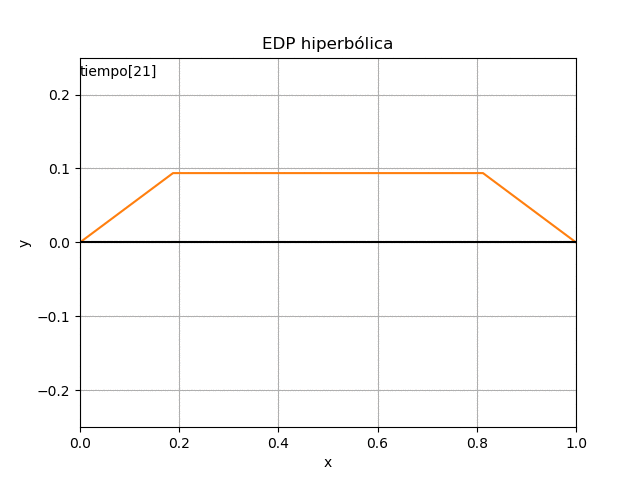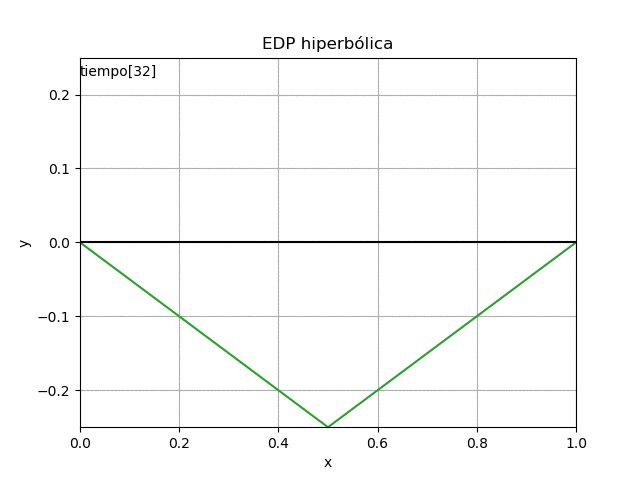
u(x,0) = \begin{cases} -0.5x &, 0\lt x\leq 0.5 \\ 0.5(x-1) &, 0.5\lt x \lt 1 \end{cases}

Se suelta la cuerda, con velocidad cero desde la posición inicial:

\frac{\partial u(x,0)}{\partial t} = 0

La solución se realiza de forma semejante al procedimiento para EDP parabólicas y elípticas. Se cambia a la forma discreta  usando diferencias finitas divididas:

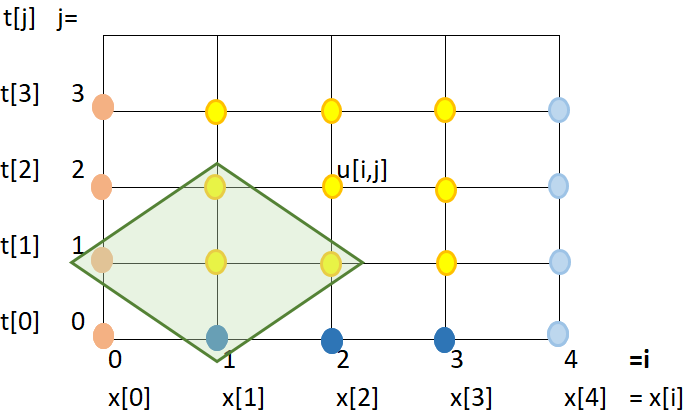
\frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{(\Delta t)^2} =c^2 \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2}

El error es del orden O(\Delta x)^2 + O(\Delta t)^2.
se reagrupa de la forma:

u_{i,j+1}-2u_{i,j}+u_{i,j-1} = \frac{c^2 (\Delta t)^2}{(\Delta x)^2} \big( u_{i+1,j}-2u_{i,j}+u_{i-1,j} \big)

El término constante, por facilidad se simplifica con el valor de 1

\lambda = \frac{c^2 (\Delta t)^2}{(\Delta x)^2} =1

si c = 2 y Δx = 0.2, se deduce que Δt = 0.1

que al sustituir en la ecuación, se simplifica anulando el término u[i,j]:

u_{i,j+1}+u_{i,j-1} = u_{i+1,j}+u_{i-1,j}

en los que intervienen solo los puntos extremos. Despejando el punto superior del rombo:

u_{i,j+1} = u_{i+1,j}-u_{i,j-1}+u_{i-1,j}

Convergencia:

\lambda = \frac{c^2 (\Delta t)^2}{(\Delta x)^2} \leq 1

para simplificar aún más el problema, se usa la condición velocidad inicial de la cuerda igual a cero

\frac{\delta u_{i,0}}{\delta t}=\frac{u_{i,1}-u_{i,-1}}{2\Delta t} = 0 u_{i,-1}=u_{i,1}

que se usa para cuando el tiempo es cero, permite calcular los puntos para t[1]:

j=0

u_{i,1} = u_{i+1,0}-u_{i,-1}+u_{i-1,0} u_{i,1} = u_{i+1,0}-u_{i,1}+u_{i-1,0} 2 u_{i,1} = u_{i+1,0}+u_{i-1,0} u_{i,1} = \frac{u_{i+1,0}+u_{i-1,0}}{2}

Aplicando solo cuando j = 0

que al ponerlos en la malla se logra un sistema explícito para cada u[i,j], con lo que se puede resolver con un algoritmo:

Algoritmo en Python:

# Ecuaciones Diferenciales Parciales
# Hiperbólica. Método explicito
import numpy as np

def cuerdainicio(xi):
    n = len(xi)
    y = np.zeros(n,dtype=float)
    for i in range(0,n,1):
        if (xi[i]<=0.5):
            y[i]=-0.5*xi[i]
        else:
            y[i]=0.5*(xi[i]-1)
    return(y)

# INGRESO
x0 = 0
xn = 1 # Longitud de cuerda
y0 = 0
yn = 0 # Puntos de amarre
t0 = 0
c = 2
# discretiza
tramosx = 16
tramost = 32
dx = (xn-x0)/tramosx 
dt = dx/c

# PROCEDIMIENTO
xi = np.arange(x0,xn+dx,dx)
tj = np.arange(0,tramost*dt+dt,dt)
n = len(xi)
m = len(tj)

u = np.zeros(shape=(n,m),dtype=float)
u[:,0] = cuerdainicio(xi)
u[0,:] = y0
u[n-1,:] = yn
# Aplicando condición inicial
j = 0
for i in range(1,n-1,1):
    u[i,j+1] = (u[i+1,j]+u[i-1,j])/2
# Para los otros puntos
for j in range(1,m-1,1):
    for i in range(1,n-1,1):
        u[i,j+1] = u[i+1,j]-u[i,j-1]+u[i-1,j]

# SALIDA
np.set_printoptions(precision=2)
print('xi =')
print(xi)
print('tj =')
print(tj)
print('matriz u =')
print(u)

con lo que se obtienen los resultados numéricos, que para mejor interpretación se presentan en una gráfica estática y otra animada.

# GRAFICA
import matplotlib.pyplot as plt

for j in range(0,m,1):
    y = u[:,j]
    plt.plot(xi,y)

plt.title('EDP hiperbólica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

# **** GRÁFICO CON ANIMACION ***********
import matplotlib.animation as animation

# Inicializa parametros de trama/foto
retardo = 70   # milisegundos entre tramas
tramas  = m
maximoy = np.max(np.abs(u))
figura, ejes = plt.subplots()
plt.xlim([x0,xn])
plt.ylim([-maximoy,maximoy])

# lineas de función y polinomio en gráfico
linea_poli, = ejes.plot(xi,u[:,0], '-')
plt.axhline(0, color='k')  # Eje en x=0

plt.title('EDP hiperbólica')
# plt.legend()
# txt_x = (x0+xn)/2
txt_y = maximoy*(1-0.1)
texto = ejes.text(x0,txt_y,'tiempo:',
                  horizontalalignment='left')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()

# Nueva Trama
def unatrama(i,xi,u):
    # actualiza cada linea
    linea_poli.set_ydata(u[:,i])
    linea_poli.set_xdata(xi)
    linea_poli.set_label('tiempo linea: '+str(i))
    texto.set_text('tiempo['+str(i)+']')
    # color de la línea
    if (i<=9):
        lineacolor = 'C'+str(i)
    else:
        numcolor = i%10
        lineacolor = 'C'+str(numcolor)
    linea_poli.set_color(lineacolor)
    return linea_poli, texto

# Limpia Trama anterior
def limpiatrama():
    linea_poli.set_ydata(np.ma.array(xi, mask=True))
    linea_poli.set_label('')
    texto.set_text('')
    return linea_poli, texto

# Trama contador
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(figura,
                              unatrama,
                              i ,
                              fargs=(xi,u),
                              init_func=limpiatrama,
                              interval=retardo,
                              blit=True)
# Graba Archivo video y GIFAnimado :
# ani.save('EDP_hiperbólica.mp4')
ani.save('EDP_hiperbolica.gif', writer='imagemagick')
plt.draw()
plt.show()

Una vez realizado el algoritmo, se pueden cambiar las condiciones iniciales de la cuerda y se observan los resultados.

Se recomienda realizar otros ejercicios de la sección de evaluaciones para EDP Hiperbólicas y observar los resultados con el algoritmo modificado.

con el resultado desarrollado en EDP elípticas para:

\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{ \partial y^2} = 0

y con el supuesto que: \lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = 1

se puede plantear que:

u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} = 0

con lo que para el método implícito, se plantea un sistema de ecuaciones para determinar los valores en cada punto desconocido.

j=1, i =1

u_{2,1}-4u_{1,1}+u_{0,1} + u_{1,2} +u_{1,0} = 0 u_{2,1}-4u_{1,1}+Ta + u_{1,2} +Tc= 0 -4u_{1,1}+u_{2,1}+u_{1,2} = -(Tc+Ta)

j=1, i =2

u_{3,1}-4u_{2,1}+u_{1,1} + u_{2,2} +u_{2,0} = 0 u_{3,1}-4u_{2,1}+u_{1,1} + u_{2,2} +Tc = 0 u_{1,1}-4u_{2,1}+u_{3,1}+ u_{2,2}= -Tc

j=1, i=3

u_{4,1}-4u_{3,1}+u_{2,1} + u_{3,2} +u_{3,0} = 0 Tb-4u_{3,1}+u_{2,1} + u_{3,2} +Tc = 0 u_{2,1} -4u_{3,1} + u_{3,2} = -(Tc+Tb)

j=2, i=1

u_{2,2}-4u_{1,2}+u_{0,2} + u_{1,3} +u_{1,1} = 0 u_{2,2}-4u_{1,2}+Ta + u_{1,3} +u_{1,1} = 0 -4u_{1,2}+u_{2,2}+u_{1,1}+u_{1,3} = -Ta

j = 2, i = 2

u_{1,2}-4u_{2,2}+u_{3,2} + u_{2,3} +u_{2,1} = 0

j = 2, i = 3

u_{4,2}-4u_{3,2}+u_{2,2} + u_{3,3} +u_{3,1} = 0 Tb-4u_{3,2}+u_{2,2} + u_{3,3} +u_{3,1} = 0 u_{2,2} -4u_{3,2}+ u_{3,3} +u_{3,1} = -Tb

j=3, i = 1

u_{2,3}-4u_{1,3}+u_{0,3} + u_{1,4} +u_{1,2} = 0 u_{2,3}-4u_{1,3}+Ta + Td +u_{1,2} = 0 -4u_{1,3}+u_{2,3}+u_{1,2} = -(Td+Ta)

j=3, i = 2

u_{3,3}-4u_{2,3}+u_{1,3} + u_{2,4} +u_{2,2} = 0 u_{3,3}-4u_{2,3}+u_{1,3} + Td +u_{2,2} = 0 +u_{1,3} -4u_{2,3}+u_{3,3} +u_{2,2} = -Td

j=3, i=3

u_{4,3}-4u_{3,3}+u_{2,3} + u_{3,4} +u_{3,2} = 0 Tb-4u_{3,3}+u_{2,3} + Td +u_{3,2} = 0 u_{2,3}-4u_{3,3}+u_{3,2} = -(Td+Tb)

con las ecuaciones se arma una matriz:

A = np.array([
    [-4, 1, 0, 1, 0, 0, 0, 0, 0],
    [ 1,-4, 1, 0, 1, 0, 0, 0, 0],
    [ 0, 1,-4, 0, 0, 1, 0, 0, 0],
    [ 1, 0, 0,-4, 1, 0, 1, 0, 0],
    [ 0, 1, 0, 1,-4, 1, 0, 1, 0],
    [ 0, 0, 1, 0, 1,-4, 0, 0, 1],
    [ 0, 0, 0, 1, 0, 0,-4, 1, 0],
    [ 0, 0, 0, 0, 1, 0, 1,-4, 1],
    [ 0, 0, 0, 0, 0, 1, 0, 1,-4],
    ])
B = np.array([-(Tc+Ta),-Tc,-(Tc+Tb),
                  -Ta,   0,    -Tb,
              -(Td+Ta),-Td,-(Td+Tb)])

que al resolver el sistema de ecuaciones se obtiene:

>>> Xu
array([ 56.43,  55.71,  56.43,  60.  ,  60.  ,  60.  ,  63.57,  64.29,
        63.57])

ingresando los resultados a la matriz u:

xi=
[ 0.   0.5  1.   1.5  2. ]
yj=
[ 0.    0.38  0.75  1.12  1.5 ]
matriz u
[[ 60.    60.    60.    60.    60.  ]
 [ 50.    56.43  60.    63.57  70.  ]
 [ 50.    55.71  60.    64.29  70.  ]
 [ 50.    56.43  60.    63.57  70.  ]
 [ 60.    60.    60.    60.    60.  ]]
>>>

Algoritmo usado para resolver el problema:

# Ecuaciones Diferenciales Parciales
# Elipticas. Método implícito
import numpy as np

# INGRESO
# Condiciones iniciales en los bordes
Ta = 60
Tb = 60
Tc = 50
Td = 70
# dimensiones de la placa
x0 = 0
xn = 2
y0 = 0
yn = 1.5
# discretiza, supone dx=dy
tramosx = 4
tramosy = 4
dx = (xn-x0)/tramosx 
dy = (yn-y0)/tramosy 
maxitera = 100
tolera = 0.0001

A = np.array([
    [-4, 1, 0, 1, 0, 0, 0, 0, 0],
    [ 1,-4, 1, 0, 1, 0, 0, 0, 0],
    [ 0, 1,-4, 0, 0, 1, 0, 0, 0],
    [ 1, 0, 0,-4, 1, 0, 1, 0, 0],
    [ 0, 1, 0, 1,-4, 1, 0, 1, 0],
    [ 0, 0, 1, 0, 1,-4, 0, 0, 1],
    [ 0, 0, 0, 1, 0, 0,-4, 1, 0],
    [ 0, 0, 0, 0, 1, 0, 1,-4, 1],
    [ 0, 0, 0, 0, 0, 1, 0, 1,-4],
    ])
B = np.array([-(Tc+Ta),-Tc,-(Tc+Tb),
              -Ta,0,-Tb,
              -(Td+Ta),-Td,-(Td+Tb)])


# PROCEDIMIENTO
# Resuelve sistema ecuaciones
Xu = np.linalg.solve(A,B)
[nx,mx] = np.shape(A)

xi = np.arange(x0,xn+dx,dx)
yj = np.arange(y0,yn+dy,dy)
n = len(xi)
m = len(yj)

u = np.zeros(shape=(n,m),dtype=float)
u[:,0]   = Tc
u[:,m-1] = Td
u[0,:]   = Ta
u[n-1,:] = Tb
u[1:1+3,1] = Xu[0:0+3]
u[1:1+3,2] = Xu[3:3+3]
u[1:1+3,3] = Xu[6:6+3]

# SALIDA
np.set_printoptions(precision=2)
print('xi=')
print(xi)
print('yj=')
print(yj)
print('matriz u')
print(u)

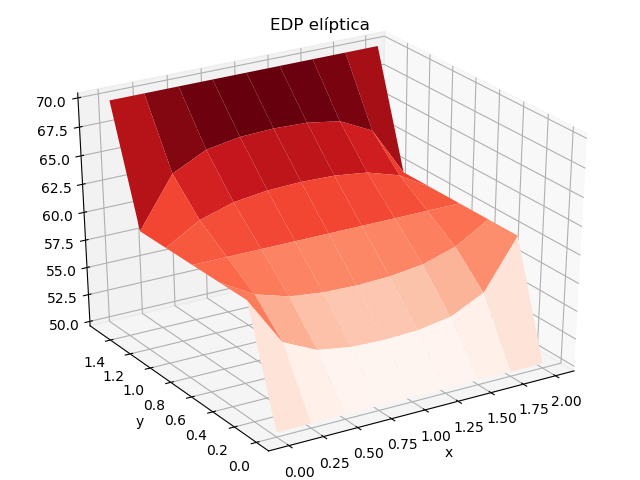
La gráfica de resultados se obtiene de forma semejante al ejercicio con método iterativo.

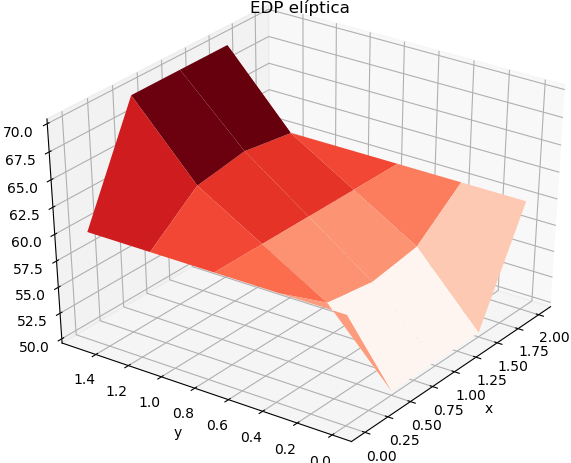
# Gráfica
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

X, Y = np.meshgrid(xi, yj)
U = np.transpose(u) # ajuste de índices fila es x

figura = plt.figure()
ax = Axes3D(figura)
ax.plot_surface(X, Y, U, rstride=1, cstride=1, cmap=cm.Reds)

plt.title('EDP elíptica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Se podría estandarizar un poco más el proceso para que sea realizado por el algoritmo y sea más sencillo generar la matriz con más puntos. Tarea.

con el resultado desarrollado en EDP elípticas para:

\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{ \partial y^2} = 0

y con el supuesto que: \lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = 1

se puede plantear que:

u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} = 0

que reordenando para un punto central desconocido se convierte a:

u_{i,j} = \frac{1}{4} \big[ u_{i+1,j}+u_{i-1,j} + u_{i,j+1} +u_{i,j-1} \big]

con lo que se interpreta que cada punto central es el resultado del promedio de los puntos alrededor del rombo formado en la malla.

El cálculo numerico se puede realizar de forma iterativa haciendo varias pasadas en la matriz, promediando cada punto. Para revisar las iteraciones se controla la convergencia junto con un máximo de iteraciones.

# Ecuaciones Diferenciales Parciales
# Elipticas. Método iterativo
import numpy as np

# INGRESO
# Condiciones iniciales en los bordes
Ta = 60
Tb = 60
Tc = 50
Td = 70
# dimensiones de la placa
x0 = 0
xn = 2
y0 = 0
yn = 1.5
# discretiza, supone dx=dy
dx = 0.25 
dy = 0.25 
maxitera = 100
tolera = 0.0001

# PROCEDIMIENTO
xi = np.arange(x0,xn+dx,dx)
yj = np.arange(y0,yn+dy,dy)
n = len(xi)
m = len(yj)
# Matriz u
u = np.zeros(shape=(n,m),dtype = float)
# valores en fronteras
u[0,:]   = Ta
u[n-1,:] = Tb
u[:,0]   = Tc
u[:,m-1] = Td

# valor inicial de iteración
promedio = (Ta+Tb+Tc+Td)/4
u[1:n-1,1:m-1] = promedio
# iterar puntos interiores
itera = 0
converge = 0
while not(itera>=maxitera or converge==1):
    itera = itera +1
    nueva = np.copy(u)
    for i in range(1,n-1):
        for j in range(1,m-1):
            u[i,j] = (u[i-1,j]+u[i+1,j]+u[i,j-1]+u[i,j+1])/4
    diferencia = nueva-u
    erroru = np.linalg.norm(np.abs(diferencia))
    if (erroru<tolera):
        converge = 1

# SALIDA
np.set_printoptions(precision=2)
print('converge = ', converge)
print('xi=')
print(xi)
print('yj=')
print(yj)
print('matriz u')
print(u)

Un ejemplo de resultados:

converge = 1
xi=
[ 0.    0.25  0.5   0.75  1.    1.25  1.5   1.75  2.  ]
yi=
[ 0.    0.25  0.5   0.75  1.    1.25  1.5 ]
matriz u
[[ 50.    60.    60.    60.    60.    60.    70.  ]
 [ 50.    55.6   58.23  60.    61.77  64.4   70.  ]
 [ 50.    54.15  57.34  60.    62.66  65.85  70.  ]
 [ 50.    53.67  56.97  60.    63.03  66.33  70.  ]
 [ 50.    53.55  56.87  60.    63.13  66.45  70.  ]
 [ 50.    53.67  56.97  60.    63.03  66.33  70.  ]
 [ 50.    54.15  57.34  60.    62.66  65.85  70.  ]
 [ 50.    55.6   58.23  60.    61.77  64.4   70.  ]
 [ 50.    60.    60.    60.    60.    60.    70.  ]]
>>>

Cuyos valores se interpretan mejor en una gráfica, en este caso 3D:

La gráfica de resultados requiere ajuste de ejes, pues el índice de filas es el eje x, y las columnas es el eje y. La matriz graficada se obtiene como la transpuesta de u

# Gráfica
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

X, Y = np.meshgrid(xi, yj)
U = np.transpose(u) # ajuste de índices fila es x

figura = plt.figure()
ax = Axes3D(figura)
ax.plot_surface(X, Y, U,
                rstride=1,
                cstride=1,
                cmap=cm.Reds)

plt.title('EDP elíptica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()