Referencia: Burden 7Ed cap 1.1 Ejercicio 8. Burden p15, 9Ed p15
Obtenga el tercer polinomio de Taylor P3(x) para la función:
f(x) = \sqrt{x+1}alrededor de x0=0.
Aproxime el resultado para x=0.5, 0.75, 1.25 y 1.75 usando P3(x) y calcule los errores reales.
1. Desarrollo analítico
Se indica calcular los errores reales como la diferencia entre f(x) y el polinomio de Taylor p(x).
Siguiendo los pasos del ejercicio01, Determine el polinomio de Taylor, realice los pasos y verifique su respuesta con:
P_3(x) = 1 + \frac{1}{2}x - \frac{1}{8} x^2 +\frac{1}{16} x^3luego calcule los valores de la tabla:
| x | P3(x) | \sqrt{x+1} | |diferencia ó error| |
|---|---|---|---|
| 0.5 | 1.22656250000000 | 1.22474487139159 | 0.00181762860841106 |
| 0.75 | |||
| 1.25 | |||
| 1.5 |
Realice las observaciones a los resultados obtenidos.
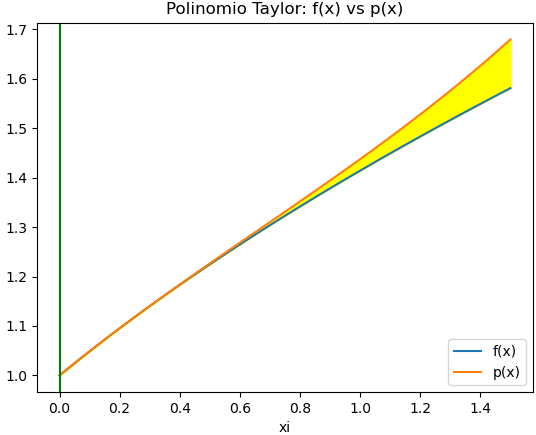
Al graficar los valores de la tabla, se tiene puede observar que al alejarse x del punto de referencia x0, el error aumenta. Se representa como lo marcado en amarillo entre las curvas f(x) y el polinomio p(x).
2. Desarrollo algorítmico, instrucciones en Python
Puede reutilizar la función del polinomio de Taylor con la fórmula simbólica usada en el enlace del Ejemplo 1.4
A partir del algoritmo básico, se convierte el procedimiento a una función def-return. Con la función politaylor() se crea el polinomio y se evalúa para calcular el error respecto al valor real de la expresión.
# Aproximación Polinomio de Taylor alrededor de x0 # función en forma simbólica con sympy import numpy as np import sympy as sym # Calcula n términos del polinomio de Taylor # funcionx es simbólica def politaylor(fx,x0,n): k = 0 polinomio = 0 while (k <= n): derivada = fx.diff(x,k) derivadax0 = derivada.subs(x,x0) divisor = np.math.factorial(k) terminok = (derivadax0/divisor)*(x-x0)**k polinomio = polinomio + terminok k = k + 1 return(polinomio) # PROGRAMA ------------- # Capitulo 1.1 Ejecicio 8, Burden p15, pdf 25 # Calcule el error con polinomio Taylor grado 3 # INGRESO # variable x es simbólica x = sym.Symbol('x') fx = sym.sqrt(x+1) x0 = 0 xi = 0.5 # donde se evalua el polinomio n = 3 # PROCEDIMIENTO # Referencia, f(xi) real fxi = fx.subs(x,xi) # Aproximado con Taylor polinomio = politaylor(fx,x0,n) pxi = polinomio.subs(x,xi) error_real = fxi - pxi # SALIDA print(' Taylor: ', polinomio) print(' xi: ', xi) print(' estimado : ', pxi) print(' real: ', fxi) print(' error real: ', error_real)
cuyo resultado para xi=0.5 es:
Taylor: x**3/16 - x**2/8 + x/2 + 1 xi: 0.5 estimado : 1.22656250000000 real: 1.22474487139159 error real: -0.00181762860841106
complete la tabla usando también el algoritmo en Python
2.1 Gráfica del Error entre f(x) y p(x)
Esta es una sección complementaria para realizar la gráfica mostrada en el ejemplo. Requiere el uso de la librería matplotlib. Puede revisar la sección de Recursos/Resumen Python/Gráficas 2D de línea para más detalles.
- Para evaluar en el intervalo se requiere convertir las expresiones simbólicas a la forma numérica lambda: fxn, pxn
- Para la gráfica, se usa el intervalo [a,b] con las muestras necesarias para una buena resolución de imagen. Se obtiene el vector xin
- Se evalua fxn y pxn en el intervalo, obteniendo los valores en los vectores: fxni y pxni.
- Se realiza la gráfica entre xin vs fxni y pxni
- Para destacar el error de truncamiento, se rellena el espacio en color amarillo entre fxni y pxni, usando
plt.fill_between(). - Para resaltar x0, se traza una línea vertical.
# cambia a forma lambda fxn = sym.lambdify(x,fx,'numpy') pxn = sym.lambdify(x,polinomio,'numpy') # intervalo usando xi como referencia a = x0 # izquierda b = x0 + 3*xi # derecha muestras = 51 # evaluar en intervalo xin = np.linspace(a,b,muestras) fxni = fxn(xin) pxni = pxn(xin) # Gráfica plt.plot(xin,fxni,label='f(x)') plt.plot(xin,pxni,label='p(x)') plt.fill_between(xin,pxni,fxni,color='yellow') plt.axvline(x0,color='green') plt.title('Polinomio Taylor: f(x) vs p(x)') plt.legend() plt.xlabel('xi') plt.show()