2da Evaluación II Término 2018-2019. 29/Enero/2019. MATG1013
Tema 1. (30 puntos) La integración proporciona un medio para calcular cuánta masa entra o sale de un reactor químico durante un periodo específico de tiempo.
M = \int^{t_2}_{t_1}Q(t)C(t) dt
t : min
C(t) : mg/m3
Q(t) : m3/min
a) Con los datos mostrados en la tabla y usando los métodos de Simpson 1/3 y 3/8, aproxime la cantidad de masa que sale de un reactor entre t1=0 y t2=25 min.
t
0
5
10
15
20
25
C(t)
10
18
27
35
40
30
Q(t)
4
6
7
6
5
5
b) Estime el error
Rúbrica: Conoce los métodos de Simpson hasta (5 puntos), Calcula la función a integrar hasta (5 puntos), Separa los intervalos hasta (5 puntos), Aplica las fórmulas correctamente hasta (5 puntos). Literal b, conoce las fórmulas del error (5 puntos), calcula los errores (5 puntos)
2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013
Tema 4. (30 puntos) Para una sección de 500 m del acceso marítimo a los puertos de Guayaquil se requiere de un canal con:
profundidad mínima de 11 metros MLWS
ancho de 250 m
de tal forma que permita navegar buques de carga de mayor tamaño.
Dispone de las mediciones de profundidad mostradas en la tabla de batimetría:
Batimetría
yi \ xi
0
50
100
150
200
250
0
-6.79
-12.03
-10.04
-11.60
-7.24
-7.91
100
-8.85
-10.89
-8.95
-7.23
-11.42
-7.93
200
-11.90
-9.86
-9.35
-12.05
-9.38
-9.65
300
-7.30
-11.55
-10.41
-8.67
-11.84
-6.77
400
-12.17
-9.62
-7.47
-6.51
-9.02
-9.60
500
-11.90
-10.23
-10.68
-9.94
-6.76
-7.46
a) Obtenga la tabla de dragado como la diferencia entre la profundidad del canal requerido y la tabla de batimetría.
b) Estime el volumen de sedimentos a remover por la draga usando integración por el método de Simpson.
Nota: Si el fondo está más allá de los 11 metros, no se requiere la intervención de la draga.
Rúbrica: literal a (5 puntos), selección apropiada del método por intervalo y aplicación en un eje (15 puntos), integración en el otro eje (5 puntos), presentar las iteraciones correctamente (5 puntos)
2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013
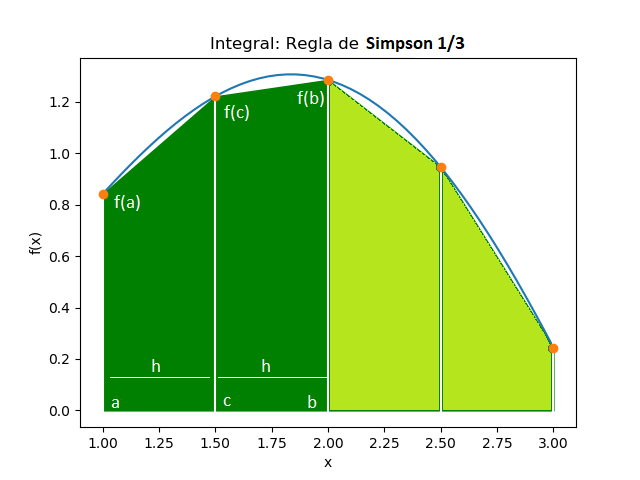
Tema 2. (20 puntos) Deduzca el método de Simpson 1/3
Sugerencias: Una de las formas de plantear la deducción es usando un polinomio de Lagrange con grado 2 para aproximar la función que pasa por los puntos [a,f(a)], [b,f(b)] y [c,f(c)].
Considere que los tramos tienen h tienen tamaño (b-a)/2, (c-a), (b-c)
Plantee la ecuación y sustituya los valores de los tramos por valores de h para resolver todo en función de h.
Rúbrica: Planteo del problema con polinomio (5 puntos), desarrollo del problema con integral (5 puntos c/u).
2da Evaluación II Término 2016-2017. 14/Febrero/2017. ICM02188 Métodos Numérico
Tema 2. En una bodega de 4 m x 6m, hay una montaña de cacao seco listo para empaque.
La tabla indica la altura en metros de la montaña sobre el nodo en el plano medido al centímetro más cercano.
f(x,y)
x=0
x=1
x=2
x=3
x=4
y=0
0.38
0.62
0.38
0.08
0.01
y=1.5
1.31
2.16
1.31
0.29
0.02
y=3
1.02
1.68
1.02
0.23
0.02
y=4.5
0.18
0.29
0.18
0.04
0.00
y=6
0.01
0.01
0.01
0.00
0.00
Use el método de Simpson 1/3 en ambas direcciones para aproximar el volumen V:
V = \int_0^4 \int_0^6 f(x,y)dydx
a) Realice la formulación del método indicando los puntos de la cuadrícula.
b) Estime la cota del error propagado y error total
Rúbrica: Planteamiento del problema (5 puntos), selección de método minimizando cotas de error (5 puntos), integración en un eje (5 puntos), integración en el otro eje (5 puntos), Estimación de errores (5 puntos)
2da Evaluación II Término 2016-2017. 14/Febrero/2017. ICM02188 Métodos Numéricos
Tema 1. El coeficiente de Gini es una medida para medir la desigualdad.
G=\frac{a}{a+b}
Donde b es el área bajo la curva de Lorentz (Porcentaje de ingresos de las personas que menos ganan f(x) versus porcentaje de la población x, a + b = 0.5
Suponga que una población tiene los siguientes ingresos:
Datos de Población
segmento (%)
20
20
20
20
20
Ingresos ($)
10000
20000
25000
30000
85000
a) Calcule los porcentajes acumulados y construya la función f(x) en función de x
(Curva de Lorentz)
b) Aproxime b = \int_0^1 f(x) dx mediante el método del trapecio,
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 1. (20 puntos) Para una fibra óptica que para por montañas se tienen las medidas de distancia vertical en función de la distancia horizontal y se muestra en la figura y la tabla.
distancias en metros
horizontal x
vertical y
0
0
100
25
200
38
300
45
400
20
a. Encuentre y' en los puntos de la tabla usando una aproximación de O(h2)
b. Usando La regla de Simpson 1/3 aproxime la longitud del cable y estime el error.
x = [ 0, 100, 200, 300, 400]
y = [ 0, 25, 38, 45, 20]
