4.2 Movimiento circular velocidad(t)- gráficas y animación con matplotlib-Python

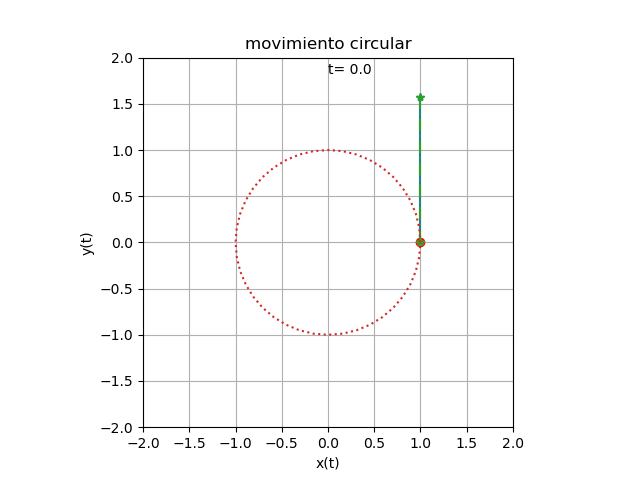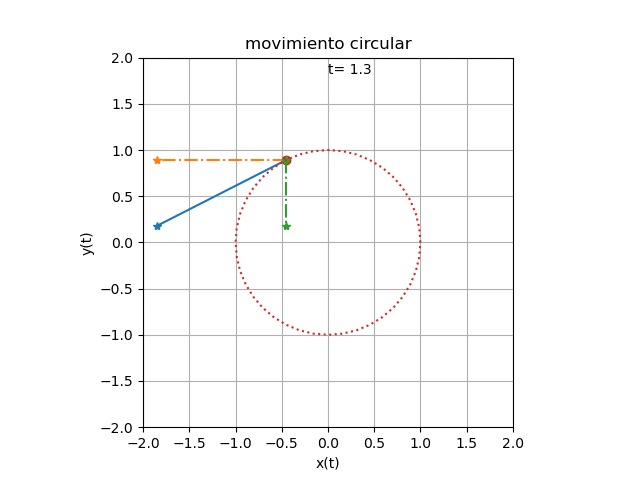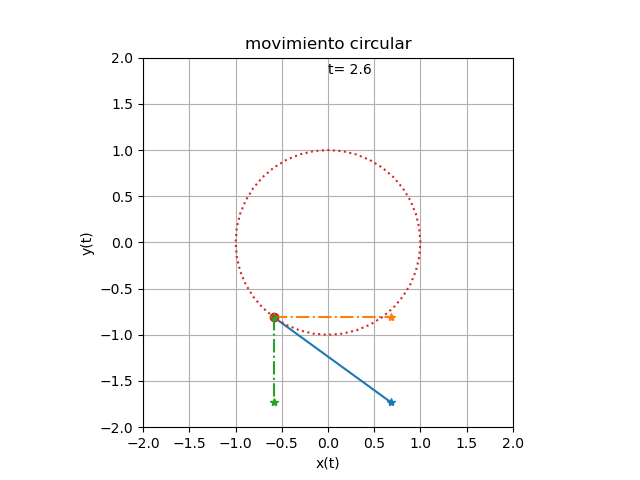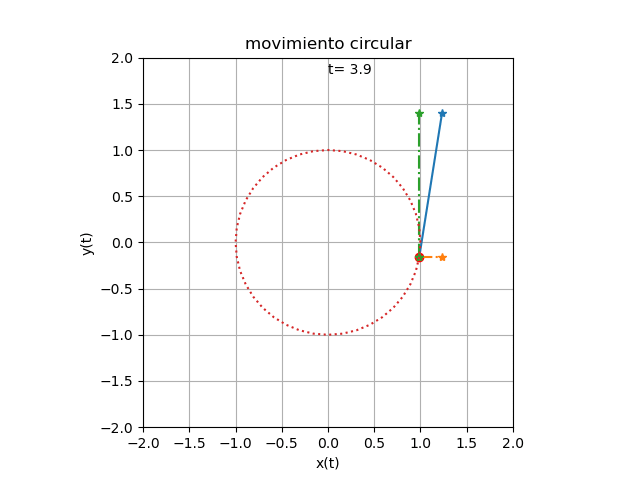
Se añaden los componentes de velocidad por cada eje al algoritmo de movimiento circular de una partícula para obtener el resultado siguiente

v_x(t) = \frac{\delta}{\delta t} x(t) =-\frac{2\pi}{T}\sin \Big( \frac{2 \pi}{T}t \Big) v_y(t) = \frac{\delta}{\delta t}y(t) = \frac{2\pi}{T}\cos\Big( \frac{2 \pi}{T}t \Big)

donde T es el periodo de la función.

Los vectores de velocidad son líneas que parten desde la posición de la partícula y se extienden en magnitud de cada componente de la velocidad

vx, = graf_xy.plot([xi[0],xi[0]+vxi[0]],
                   [yi[0],yi[0]],'*-.')
vy, = graf_xy.plot([xi[0],xi[0]],
                   [yi[0],yi[0]+vyi[0]],'*-.')

en cada procedimiento redibuja(i) y borrapizarra() se incorpora el nuevo componente para actualizar las coordenadas y en la salida return().

Al incorporar los vectores de velocidad, se debe extender los intervalos de cada eje, con un exceso de 0.2 como espacio para mostrar el cuadro de texto para la variable tiempo.

Instrucciones en Python

# FCNM-ESPOL-2015. Fisica con Python
# velocidad de una particula en recorrido circular
# propuesta: edelros@espol.edu.ec

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# INGRESO
T = 4 # periodo en segundos
x_t = lambda t: np.cos(2*np.pi*t/T)
y_t = lambda t: np.sin(2*np.pi*t/T)
# velocidades
v_x = lambda t: -(2*np.pi/T)*np.sin(2*np.pi*t/T)
v_y = lambda t: (2*np.pi/T)*np.cos(2*np.pi*t/T)

# intervalos ejes x,y 
x_a = -1.8-.2 ; x_b =-x_a  # simétricos a 0
y_a = -1.8-.2 ; y_b =-y_a

fotos  = 40   # muestras en un periodo
retardo = int(T/fotos*1000)  # milisegundos entre fotogramas

narchivo = 'movimientocircular02' # archivo.gif

# PROCEDIMIENTO
# Inicializa valores de muestras
i  = np.arange(0, fotos) # cuenta tramas
ti = np.linspace(0,T,fotos+1)
xi = x_t(ti)
yi = y_t(ti)
vxi = v_x(ti)
vyi = v_y(ti)

# SALIDA - Gráfica animada
figura, graf_xy = plt.subplots()
graf_xy.axis([x_a, x_b, y_a, y_b])
graf_xy.set_aspect('equal')
graf_xy.grid()
graf_xy.set_xlabel('x(t)')
graf_xy.set_ylabel('y(t)')
graf_xy.set_title('movimiento circular')
punto, = graf_xy.plot(xi[0], yi[0],'ro')
# dibuja velocidad
velocidad, = graf_xy.plot([xi[0],xi[0]+vxi[0]],
                          [yi[0],yi[0]+vyi[0]],'*-')
vx, = graf_xy.plot([xi[0],xi[0]+vxi[0]],
                   [yi[0],yi[0]],'*-.')
vy, = graf_xy.plot([xi[0],xi[0]],
                   [yi[0],yi[0]+vyi[0]],'*-.')

# Dibuja trayectoria circular
trayecto = graf_xy.plot(xi,yi,linestyle='dotted')


# cuadros de texto en gráfico
txt_x = (x_b+x_a)/2
txt_y = y_b*(1-0.09)
txt_ti = graf_xy.text(txt_x,txt_y,'t='+str(ti[0]),
                      horizontalalignment='left')

# Animación Nueva graf_xy (n frame)
def redibuja(i):
    # actualiza el punto
    punto.set_xdata(xi[i]) 
    punto.set_ydata(yi[i])
    # actualiza velocidad
    velocidad.set_xdata([xi[i],xi[i]+vxi[i]])
    velocidad.set_ydata([yi[i],yi[i]+vyi[i]])
    vx.set_xdata([xi[i],xi[i]+vxi[i]])
    vx.set_ydata([yi[i],yi[i]])
    vy.set_xdata([xi[i],xi[i]])
    vy.set_ydata([yi[i],yi[i]+vyi[i]])
    
    # actualiza texto
    t_trama = np.around(ti[i],2)
    txt_ti.set_text('t= '+str(t_trama))
    return (punto,txt_ti,velocidad,vx,vy)

def borrapizarra(): # limpiar gráfica
    punto.set_ydata(np.ma.array(xi, mask=True))
    velocidad.set_ydata(np.ma.array(xi, mask=True))
    vx.set_ydata(np.ma.array(xi, mask=True))
    vy.set_ydata(np.ma.array(xi, mask=True))
    txt_ti.set_text('')
    return (punto,txt_ti,velocidad,vx,vy)

# Animación coordina
ani = animation.FuncAnimation(figura, redibuja, i ,
                              init_func=borrapizarra,
                              interval = retardo, blit=True)
# Graba Archivo GIFAnimado y video, requiere 'imagemagick'
ani.save(narchivo+'_GIFanimado.gif',writer='imagemagick')

plt.show()