Referencia: Sears-Zemansky Cap33.2 Vol2 Ed.12 p1123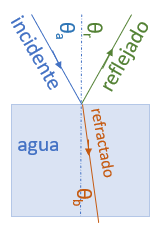
El modelo de luz basado en rayos permite describir la propagación por: reflexión y refracción.
Un rayo de onda luminosa que incide en una material liso que separa dos materiales transparentes (como el aire y el vidrio o el agua y el vidrio), el rayo es reflejado parcialmente y también refractado parcialmente hacia el segundo material.
Los rayos incidente, reflejado y refractado en una interfaz lisa entre dos materiales ópticos forman ángulos θa,θr,θb respecto a la normal (perpendicular) a la superficie en el punto de incidencia se ilustra en la figura. Si la superficie es rugosa, tanto la luz transmitida como la reflejada se dispersan en varias direcciones y no hay un ángulo único de transmisión o reflexión.
La reflexión con un ángulo definido desde una superficie muy lisa se llama reflexión especular ( latin de “espejo”). La reflexión dispersa a partir de una superficie áspera se llama reflexión difusa.
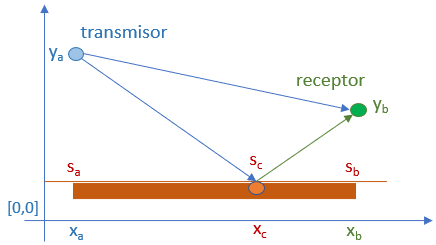
Propagación multitrayecto o multicamino en plano horizontal
Referencia: Propagación multicamino
En telecomunicaciones, la propagación de ondas de radio presentan un comportamiento semejante al de la luz para reflexión conocido como propagación multicamino o multitrayecto.
El fenómeno se da cuando las señales de radio llegan a la antena receptora por dos o más caminos y en diferentes tiempos.
La propagación mutitrayecto puede causar problemas en la recepción de la señal, debido a la interacción entre las señales recibidas. A fines prácticos, la señal obtenida en recepción difiere de la original y causa efectos que se han de compensar.
Ejercicio con gráfica
Realizar la gráfica de los rayos incidente, reflejado y directo entre el transmisor y receptor con antenas a diferentes alturas, semejante a la gráfica anterior.
 Desarrollo
Desarrollo
Si los ángulos incidente y reflejado son iguales, la pendiente rayo incidente debe ser igual en magnitud a la pendiente del rayo reflejado. Las pendientes tienen signo opuesto, el rayo izquierdo tiene pendiente negativa.
- \frac{\Delta y_{izquierda}} {\Delta x_{izquierda}} = \frac{\Delta y_{derecha}}{\Delta x_{derecha}} - \frac{s_c-y_a}{x_c-x_a} = \frac{y_b-s_c}{x_b-x_c}Por facilidad de la ecuación, se supondrá que el suelo es paralelo al eje x, a una altura sc del eje de referencia.
Se debe obtener el valor de xc de la ecuación anterior, que realizando un poco de trabajo se obtiene que:
- (x_b-x_c)(s_c-y_a) = (x_c-x_a)(y_b-s_c) - x_b(s_c-y_a) + x_c (s_c-y_a) = x_c (y_b-s_c)-x_a (y_b-s_c) x_c (s_c-y_a) - x_c (y_b-s_c)= -x_a (y_b-s_c) + x_b(s_c-y_a) x_c (2s_c-y_a-y_b)= -x_a (y_b-s_c) + x_b(s_c-y_a) x_c = \frac{x_b(s_c-y_a)-x_a(y_b-s_c)}{2s_c-y_a-y_b}Obtenido el punto xc y dado que el plano es horizontal, la altura sc es constante.
Con el algoritmo se puede obtener el punto de reflexión para varias alturas de antena y varias alturas del plano.
resultado con datos muestra:
punto reflejado: [ 8.5 , 1 ]
Instrucciones en Python
# rayo incidente y reflejado # blog.espol.edu.ec/ccpg1001 import numpy as np import matplotlib.pyplot as plt # INGRESO # posición de antenas xa = 1 # Izquierda ya = 4 xb = 11 # Derecha yb = 2 # plano el suelo sc = 1 # altura # muestras en grafica muestras = 21 # PROCEDIMIENTO numerador = xb*(sc-ya)-xa*(yb-sc) denominador = 2*sc-ya-yb xc = numerador/denominador # SALIDA print('punto reflejado: [',xc,',',sc,']') # GRAFICA #puntos en el plano plt.scatter([xa,xc,xb],[ya,sc,yb]) plt.scatter([xc],[sc],label='punto reflejo') # lineas de rayos plt.plot([xa,xc],[ya,sc],label='incidende') plt.plot([xc,xb],[sc,yb],label='reflejado') plt.plot([xa,xb],[sc,sc],label='suelo') # etiquetas anotadas plt.annotate(' reflejo',[xc,sc]) # etiquetas plt.legend() plt.xlabel('x') plt.ylabel('y') plt.title('reflexión de rayos en plano') plt.grid() plt.show()
Tarea:
a) Añadir la trayectoria directa del rayo entre el transmisor y receptor
b) Considerar que el plano puede estar inclinado respecto al eje de las x,por lo que para igualar las pendientes del rayo incidente y reflejado se referencian con la pendiente del plano.
m_s = \frac{\Delta suelo } {\Delta x_{intervalo}} = \frac{s_b-s_a}{x_b-x_a} -(m_z-m_s) = m_r-m_s -m_z = m_r - 2 m_s