s1Eva_IIT2014_T2 Triángulos aleatorios en rectángulo

Ejercicios: 1Eva_IIT2014_T2 Triángulos aleatorios en rectángulo

Propuesta de solución en Python, también se adjunta el diagrama en pdf

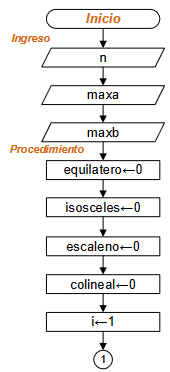
Para iniciar el ejercicio, se requiere la cantidad n de triángulos a generar y los límites del plano donde se generan [maxa,maxb]

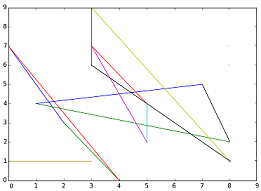
Para cada triángulo se generan las coordenadas de los vértices (xi,yi), usando números aleatorios ajustados a los límites del plano.

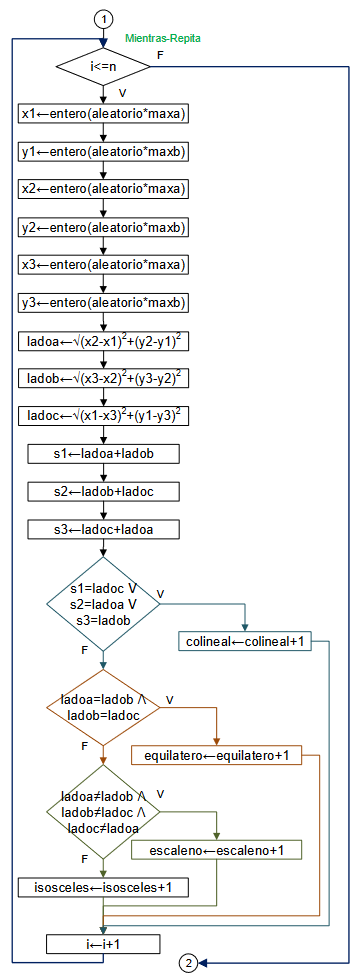
Lo más importante para este ejercicio es determinar las distancias entre los vértices, pues con ellas se determina el tipo de triángulo, siguiento las reglas básicas de la geometría.

Puede darse el caso que los puntos se encuentren en una sola línea en el plano, el caso se verifica al revisar si la suma de la longitud de dos lados es la longitud del tercer lado. Comprobar en todas las combinaciones ésta situación.

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2014_T2 Triángulos aleatorios en rectángulo
# Propuesta de solución: edelros@espol.edu.ec

import numpy as np
import random as rnd
import matplotlib.pyplot as plt

# INGRESO
n = int(input(" cuántos triángulos: "))
maxa = int(input(" rango lado a: "))
maxb = int(input(" rango lado b: "))

# PROCEDIMIENTO
equilatero = 0
isosceles  = 0
escaleno   = 0
colineal   = 0

i = 1
while (i<=n):
    
    # puntos aleatorios
    x1 = int(rnd.random()*maxa) +0
    y1 = int(rnd.random()*maxb) +0
    
    x2 = int(rnd.random()*maxa) +0
    y2 = int(rnd.random()*maxb) +0

    x3 = int(rnd.random()*maxa) +0
    y3 = int(rnd.random()*maxb) +0

    # distancias entre puntos
    a = np.sqrt((x2-x1)**2 + (y2-y1)**2)
    b = np.sqrt((x3-x2)**2 + (y3-y2)**2)
    c = np.sqrt((x1-x3)**2 + (y1-y3)**2)

    # realiza la gráfica de cada triángulo
    plt.plot([x1, x2], [y1, y2])
    plt.plot([x2, x3], [y2, y3])
    plt.plot([x1, x3], [y1, y3])

    # clasifica triángulos
    s1 = a + b
    s2 = b + c
    s3 = c + a
    if (s1==c or s2==a or s3==b):
        colineal = colineal + 1
    else:
        if (a==b and b==c):
            equilatero = equilatero+1
        else:
            if (a!=b and b!=c and c!=a):
                escaleno = escaleno+1
            else:
                isosceles = isosceles+1
    i=i+1

# SALIDA
print("equilateros: ")
print(equilatero)
print("escalenos: ")
print(escaleno)
print("isosceles: ")
print(isosceles)
print("colineales: ")
print(colineal)

# muestra la gráfica
plt.show()

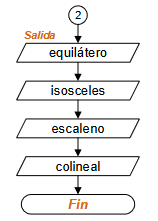
Resultado del algoritmo

 cuántos triángulos: 100
 rango lado a: 10
 rango lado b: 10
equilateros: 
0
escalenos: 
90
isosceles: 
4
colineales: 
6
>>>
 cuántos triángulos: 100
 rango lado a: 10
 rango lado b: 10
equilateros: 
0
escalenos: 
87
isosceles: 
6
colineales: 
7
>>> 

---

Diagrama de Flujo

ejercicios resueltos Python 1eva_iit2014_t2 pdf